Essential skills workbook for trades (with answer guide)
On this page
Alternate formats

Essential skills workbook for trades (with answer guide)[PDF - 2.5 MB]
Large print, braille, MP3 (audio), e-text and DAISY formats are available on demand by ordering online or calling 1 800 O-Canada (1-800-622-6232). If you use a teletypewriter (TTY), call 1-800-926-9105.
This workbook will help you practice your reading, writing, numeracy and document use skills through a variety of exercises. An answer guide is included to help you understand how to reach the right answer.
Introduction
Having strong essential skills such as reading, writing, numeracy and document use will help you succeed on the job.
The 9 essential skills are:
- Reading
- Document use
- Numeracy
- Writing
- Oral communication
- Working with others
- Thinking
- Computer use
- Continuous learning
What are essential skills?
Essential skills are used in all trades, in different ways and at different levels of complexity. Here are some examples:
- Reading and understanding specification sheets, manuals and code books
- Entering numbers and information into tables, checklists and forms
- Making calculations using formulas
- Writing short notes in logbooks and completing incident reports
- Talking to others to share information, coordinate work, ask questions and discuss issues
- Resolving problems using a troubleshooting process
- Using a computer to look up information, write an email or create a spreadsheet
- Participating in training and mentoring
Using this workbook
Use this workbook to help you identify which of your essential skills are strong and which may need improvement. The workbook includes exercises that look at 4 of the 9 essential skills (reading, document use, numeracy and writing) and provides examples of how the skills are used in the skilled trades.
Instructions:
1. Review the Tips for completing this workbook.
2. Read each question carefully. Check to see if there is any additional information required. Refer to the Formula and Conversion Sheet to help with some questions in the numeracy section.
3. Write your answers in the space provided. For the questions in the numeracy section, be sure to include all your calculations.
4. Try to complete as many questions as you can. If you do not know the answer to a question, make a note of it so you can return to it later.
5. Check your answers against the Answer Guide and make a note of areas that may need improvement.
Tips for completing this workbook
1) Skim
Skim through everything
Look over the entire workbook to get an idea of everything that is in it.
Consider these questions:
- How are the questions set up
- What symbols and words are important
- What skills will I need to use
- How does this relate to what I have learned before
2) Read
Read each question
Carefully read through each question and consider these questions:
- What is this question asking or looking for
- How does this information relate to what I already know
- What words will help me to identify relevant information and answer the question
- What words tell me about the task I need to complete
3) Answer
Answer each question
Make and carry out a plan for each question. Consider:
- What actions should I take to find the answer
- What math steps might I need to follow? Is there a formula I need to use
- What is the next logical step
- How does information relate to what I already know
- What conclusion can I make
- Have I completed the question
4) Check
Check each answer
Double check your answer by reviewing your work
- Does this answer make sense
- Does this answer need a number, A word, A sentence
- Have I given a complete answer
Reading
Understanding material written in sentences and paragraphs that may be found in reports, memos and manuals.
Read the following safety and health information and then answer the questions.
Material Safety Data Sheet (MSDS) – A safe read
In Canada, every material that is controlled by the Workplace Hazardous Materials Information System (WHMIS) must be labelled and have an accompanying Material Safety Data Sheet (MSDS) that is specific to the product or material. Both the product name and supplier on the MSDS must match the material in use. An MSDS is a document prepared by the chemical manufacturer or supplier that contains information on the potential health, fire and reactivity hazards of the product. The MSDS also describes how to use, store and handle the product safely and what to do in an emergency. It tells how to recognize symptoms of exposure and what first aid and other procedures might be necessary.
MSDSs come from many sources and may not all look the same, but they must include these 9 categories of information
1. Product information – for example, product identifier (name), manufacturer and supplier’s names, addresses and emergency telephone numbers
2. Hazardous ingredients
3. Physical data – for example, physical state, odour and boiling point
4. Fire or explosion hazard data
5. Reactivity data – for example, conditions under which the product is chemically unstable and the names of other substances the product is incompatible with
6. Toxicological properties – health effects
7. Preventive measures – for example, personal protective equipment and engineering controls
8. First aid measures
9. Preparation information
The law doesn’t expect you to know everything about all chemicals, but you must get to know the hazards, control measures and emergency procedures for each chemical product you work with. Familiarize yourself with this information from the MSDS before you start to use the product. In addition, your employer should supplement the MSDS information with site-specific information and training regarding first aid measures, hazard controls (for example, required ventilation, gloves) and what to do in case of an emergency (for example, spill or leak).
The Controlled Products Regulations specify that an MSDS for a controlled product must be no more than 3 years old. It’s up to the supplier to update the product label and MSDS. Employers must ensure that every controlled product entering the workplace is accompanied by a current MSDS. The company’s MSDS collection must be widely accessible to workers who may be exposed to the controlled products, and to the health and safety committee or representative. They can be stored in a binder or digitally on a computer network, as long as everyone in the workplace has easy access to them at all times.
The Canadian Centre for Occupational Health and Safety (CCOHS) – e-Newsletter, December 2007
1. What 2 things must an employer do with materials controlled by the Workplace Hazardous Materials Information System (WHMIS)?
2. Why do you think reactivity data information must be listed on each Material Safety Data Sheet (MSDS)?
3. How often must each MSDS be updated for a controlled product?
4. Why is it important for all employees to have access to MSDS information?
-
Answer
- Materials controlled by WHMIS must be labelled and have an accompanying MSDS that is specific to the product or material.
- The reactivity data information is included because you need to know conditions under which the,product is chemically unstable and the names of other substances the product is incompatible with.
- MSDS must be updated at least every three years.
- Employees need access to the MSDS information because they need to know about the hazards of the chemicals they may be exposed to, as well as the safe usage, storage and handling of the product. Also, they must be able to recognize the symptoms of exposure and the first-aid response.
Document use
Finding, understanding or entering information such as text, symbols and numbers in documents such as tables or forms.
WHMIS symbols
Look at the following health and safety poster and answer the questions on the following page.

-
Text version
A WHMIS poster with the title Do You Know These Vital Signs?: The Hazard Symbols of WHMIS
There are 8 hazard symbols on the poster:
- Top left circle: An image of a canister of compressed gas that indicates Class A Compressed Gas.
- Upper right circle: A capital letter T where the bottom of the T is an exclamation mark. This symbol signifies Class D-2 Poisonous and Infectious Material. Material causing other toxic effects.
- Second left circle: An image of flames above a line. This symbol signifies Class B Flammable and Combustible Material.
- Second right circle: 3 circles intersecting with a central circle. This symbol signifies Class D-3 Poisonous and Infectious Material. Biohazardous Infectious Material.
- Third left circle: An image of flames coming out of an O on top of a line. This symbol signifies Class C Oxidizing Material.
- Third right circle: An image with liquid spilling out of a container and causing corrosion to a solid object and a hand. This symbol signifies Class E Corrosive Material.
- Last left circle: An image of a skull and crossbones that indicates Class D-1 Poisonous and Infectious material. Material causing immediate and serious effects.
- Last right circle: An image of a test tube embedded in the letter R. There is liquid in the test tube and it is emitting rays. This symbol signifies Class F Dangerously Reactive Material.
WHMIS provides you with information on the safe use, storage, handling and disposal of hazardous materials at Canadian workplaces.
- Bottom left: Logo for the Workplace Hazardous Materials Information System.
- Bottom right: For more information, consult MSDS, and visit the Health Canada WHMIS Web site.
1. What does “WHMIS” stand for?
2. What harm can corrosive materials have on your skin?
3. Class D-1 deals with poisonous and infectious materials. How soon after contact with these materials would you see a reaction?
4. If you worked with materials labelled with the following symbol, what precautions would you take?

-
Answer
Question 1. A line points to the WHMIS logo in the bottom left corner. WHMIS stands for Workplace Hazardous Materials Information System
Question 2. A line points to an image with liquid spilling out of a container and causing corrosion to a solid object and a hand. This image represents Class E corrosive material. Corrosive materials can burn skin.
Question 3. A line points to an image of a skull and crossbones that represents Class D-1 Poisonous and infectious material. Material causing immediate and serious effects. Contact with poisonous and infectious materials can produce an immediate and serious reaction
Question 4. A line points to an image of flames above a line that represents Class B Flammable and Combustible Material. Materials labelled with the flammable or combustible symbol should be kept away from open flame or high heat.
Numeracy
Using numbers to solve problems and complete tasks.
Answer the following questions. Be sure to show your work. You may use a calculator unless the instructions state you should not.
Basic math
1. You should not use a calculator for this section.
- 9 + 84 =
- 72 - 35 =
- 25 x 15 =
- 36 ÷ 9 =
- 7.6 + 3.2 =
- 12.4 - 2.7
- 7.0 x 0.25 =
- 14 ÷ 0.5 =
-
Answer
- 93
- 37
- 375
- 4
- 10.8
- 9.7
- 1.75
- 28
Equivalent fractions, decimals and percentages
2. Fill in each of the missing values.
| Fraction | Decimal | Percentage | |||
|---|---|---|---|---|---|
| a. | 5/8 = /16 | = | 0. | = | % |
| b. | 9/12 = /4 | = | 0. | = | % |
| c. | 3/16 = /64 | = | 0. | = | % |
| d. | 10/12 = /36 | = | 0. | = | % |
| e. | 2/5 = /40 | = | 0. | = | % |
-
Answer
Example Fraction Decimal Percentage a. 5/8 × 2/2 = 10/16 =
0.625 × 100 =
62.5% b. 9/12 × 3/3 = 3/4 =
0.75 × 100 =
75% c. 3/16 × 4/4 = 12/64 =
0.1875 × 100 =
18.75% d. 10/12 × 3/3 = 30/36 =
0.8333 × 100 =
83.33% e. 2/5 × 8/8 = 16/40 =
0.4 × 100 =
40% How to reach the answers
When you change to equivalent fractions, you must begin by making the denominators (the bottom part of the fractions) the same. Then, whatever you do to one denominator to make it the same as the other denominator, you must also do to the numerator (top part of the fraction) of the same fraction.
In the example below, multiply the denominator of 8 by 2 to get 16 (the same as the other denominator as the other fraction), then multiply the numerator by that same number, in this case 2. This creates an equivalent fraction with a denominator of 16.
5/8 × 2/2 = 10/16
To find the decimal, divide the denominator by the numerator.
To change a decimal to a percentage, you must multiply the decimal by 100.0.625 x 100 = 62.5%
Basic operations with fractions
3. You should not use a calculator for this section.
- 1/2 + 3/4 =
- 17/32 - 5/16 =
- 215/16 + 15/8 =
- 1/4 - 9/16 =
- 33/16 - 17/8 =
- 21/2 + 5/16 =
- 3/4 × 1/2 =
- 21/2 × 8 =
- 220 ÷ 3/4 =
- 11/16 ÷ 1/8 =
-
Answer
- 11/4
- 7/32
- 49/16
- 11/16
- 15/16
- 213/16
- 3/8
- 20
- 2931/3
- 51/2
How to reach the answers
When you are adding and subtracting fractions it is necessary to get a common denominator (the same number in each denominator). You get a common denominator by multiplying in a similar manner as in section 2.a. 1/2 × (2/2) = 2/4 + 3/4 = 11/4
b. 17/32 - 5/16 × (2/2) = 17/32 - 10/32 = 7/32
When a fraction has whole numbers in addition to fractions, you can simply add or subtract the whole numbers in the final step of the problem. If you get a final answer that is greater than 1, then you will need to express it as a mixed fraction and add the whole number to the other whole numbers in the equation.
c. 215/16 + 15/8 = 215/16 + 15/8(2/2) = 215/16 + 110/16 = 325/16 = 49/16
When you are subtracting fractions, sometimes it is necessary to change a mixed fraction into an improper fraction. (See d below)
d. 11/4 - 9/16 = 11/4 × (4/4) - 9/16 = 14/16 - 9/16 = 20/16 - 9/16 = 11/16
e. 33/16 - 17/8 = 33/16 - 17/8 (2/2) = 33/16 - 114/16 = 219/16 - 114/16 = 15/16
f. 21/2 + 5/16 = 21/2 (8/8) + 5/16 = 28/16 + 5/16 = 213/16
When you are multiplying fractions you must multiply straight across the numerator and straight across the denominator of each fraction. It might be necessary to change the fraction into an improper fraction, multiply and then reduce. (See h below)
g. 3/4 × 1/2 = (3 × 1)/4 × 2 = 3/8
h. 21/2 = (2 × 2 + 1)/2 = 5/2 × 8 = 5/2 × 8/1 = 5 × 8/2 × 1 = 40/2 = 20
When you are dividing fractions you change the sign from division to multiplication and invert the fraction you are dividing by. Another way this is described is multiplying by the reciprocal.
i. 220 ÷ 3/4 = 220 × 4/3 = 220/1× 4/3 = (220 × 4)/3 × 1 = 880/3 = 2931/3
j. 11/16 ÷ 1/8 = 11/16 × 8/1 = 88/16 = 44/8 = 22/4 = 11/2 =51/2
Conversions
4. Fill in each of the missing values.
- 1440 minutes = hours
- 220 inches = feet inches
- 2.5 hours = minutes
- 90 inches = cm
- 1 fluid cup = ounces
- 120 mm = cm
-
Answer
How to reach the answers
When you are converting from one unit to another you must multiply the given quantity by an equivalent fraction that has the original units in the denominator and the desired units in the numerator. If the original units appear in the numerator and the denominator, then they will cancel each other out and leave only the desired unit.
Example: Convert 4 days into minutes.
4 days/1 x 24 hours/1 day x 60 min/1 hour = 4 x 24 x 60 min = 5 760
Notice that the units of 'days' will cancel (the unit is in the numerator and denominator) and the units of 'hours' will also cancel. This leaves the desired unit of minutes in the numerator. Multiply all of the numbers together to get 5 760 minutes.
a. 1 440 min/1 × 1 hour/60 min = 24 hours
b. 220 inches/1 × 1 foot/12 inches = 18.333 feet = 18 feet 4 inches
c. 2.5 hours/1 × 60 min/1 hour = 150 minutes
d. 90 inches/1 × 2.54 cm/1 inch = 228.6 cm
e. 1 fluid cup/1 × 8 ounces/1 fluid cup = 8 ounces
f. 120 mm/1 × 1 cm/10 mm = 12 cm
Word problems
5. Please answer the following questions about a first-year apprentice’s rate of pay and earnings. The minimum wage rate for a first-year apprentice is 180 percent of a province’s minimum wage, which is $8.50 an hour.
- What is the hourly wage for a first-year apprentice?
- Using the hours listed in the following table, what was the first-year apprentice’s pay for the week?
Schedule Monday 7.25 hours Tuesday 6.0 hours Wednesday 11.25 hours Thursday 10.5 hours Friday 5.0 hours - The overtime rate of pay per hour is “time and a half.” What would the first-year apprentice be paid per hour when working overtime?
-
Answer
a. Since percentage is really just a fraction that has a denominator of 100, 180% is 180/100.
$8.50 x 180/100 = $15.30
b. Add up all the hours for the week.
7.25 + 6.0 + 11.25 + 10.5 + 5.0 = 40 hours
40 hours x $15.30 = $612.00
c. Time and a half would be 1.5 times your hourly wage.
1.5 x $15.30 = $22.95 per hour
6. You filled up the gas tank with 75L (litres) of fuel at $1.24/L (per litre). The attendant gives you a 4 percent discount. How much will you pay, in total, for the gas?
-
Answer
The total cost would be 75 litres x $1.24 per litre = $93.00. With a 4% discount deducted from the bill, the total is $93.00 – $3.72 = $89.28.
7. A vehicle travelled 33 000 km (kilometres) in 2 years.
- The oil is changed every 5 000 km. Each oil change uses 5 litres of oil. How many litres of oil were used in total?
- At the same usage rate, if a vehicle travels 33 000 km in 2 years, how many kilometres will the vehicle have travelled in 10 years?
-
Answer
a. If an oil change is done every 5 000 km, then there would have been 33 000/5 000= 6.6 oil changes in total.
Since we cannot have part of an oil change, then we would be in between our sixth and seventh oil change. There would have been 6 actual oil changes. If there are 5 litres of oil used per oil change, then there would have been 6 oil changes x 5 L per oil change = 30 L of oil in total.
b. 33 000/2 years = 16 500/year
16 500 x 10 years = 165 000 km
Basic geometry
Show your work in the space provided below each question. The Formula and Conversion Sheet is a helpful tool for this section.
8. Refer to the following figure to answer the questions below.
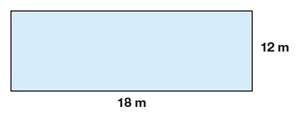
- What is the perimeter of this rectangle?
- What is the area of this rectangle?
-
Answer
a. The perimeter of any object is the distance around the outside of that object. In this case,
perimeter P = 2 (l + w).
P = 2 (12 m + 18 m) = 60 m
b. The area is A = l x w = 12 m x 18 m = 216 m2
9. The radius of the circle below is 4 cm, as shown.
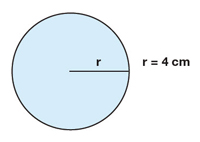
- What is the diameter of this circle?
- What is the circumference of this circle?
- What is the area of this circle?
-
Answer
a. The radius is half the length of the diameter. Since r = 4 cm, the diameter will be 2 x 4 cm = 8 cm.
b. The circumference of a circle is the distance around the outside (it is the perimeter of the circle).
Perimeter = Circumference = 2 ? r = 2(3.14)(4 cm) = 25.12 cm.
c. Area = ? r2 = ? (4 cm)2 = 50.24 cm2
A = 3.14 x (4) x (4)
A = 3.14 x 16
A = 50.24 cm2
Notice that area is two-dimensional and therefore has square units (cm2).
10. What is the volume of this figure?
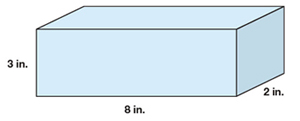
-
Answer
Volume = 48 in.3
How to reach the answer
Volume is the amount of space an object takes up.
V = l x w x h = 8 x 2 x 3 = 48 in.3
Notice that volume is a three-dimensional measure and therefore has cubic units (in.3).
11. Consider this right-angled triangle to answer the questions that follow.
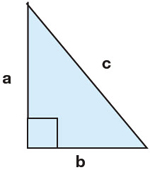
side a = 12 m and side b = 9 m
- How long is side c?
- Place an “S” on the diagram to show the smallest angle of the triangle.
- In degrees, what is the smallest angle in the triangle?
-
Answer
a. Use the Pythagorean Theorem ( a2 + b2 = c2) to solve for side c. Remember: side c is the hypotenuse which is always opposite the right angle.
12 m2 + 9 m2 = c2
144 m + 81 m = c2
225 m = c2
15 m = c
b.
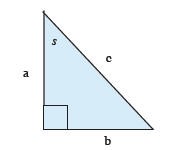
How to reach the answer
The smallest angle of any triangle is opposite the smallest or shortest side in the triangle, and the largest angle is always opposite the longest side.
c. Using right angled trigonometry:
tan S = Opposite/Adjacent
tan S = 9/12
tan -1 = (9/12) = S
S = 36.87°
12. Consider another right-angled triangle.
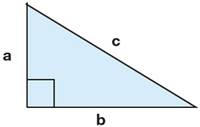
side a = 9 cm and side c = 41 cm
- How long is side b?
- Place an “S” on the diagram to show the smallest angle of the triangle.
-
Answer
a) side b = 40 cm
How to reach the answer
9 cm2 + b2 = 41 cm2
b2 = 1681 cm - 81 cm
b2 = 1600 cm
b = 40 cm
b)
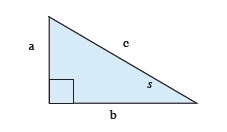
13. What is the volume of the shape below? The radius is 8 inches and the height is 10 inches. Include units in your answer.

-
Answer
Volume = 2 009.6 in.3
How to reach the answer
V = p r2hV = 3.14 (8 in.)2 (10 in.)
V = 2 009.6 in.3
Basic measurements
14. Indicate 3/4 of an inch and 2 15/16 inches on the ruler below. (Ruler is not to scale)

-
Answer
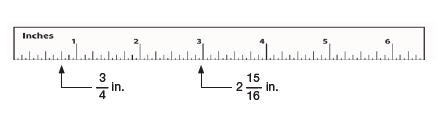
15. Indicate 87 mm and 4.3 cm on the ruler below. (Ruler is not to scale)

-
Answer

16. Indicate a measure of 47 degrees on the protractor below.
-
Answer
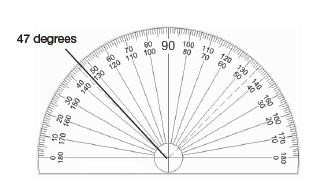
Ratio, proportion and statistics
17. Fill in the blank for each of the following:
- 3:1 = _____ : 4
- 5:6 = _____ : 3
- 6.5:3 = ____ : 9
- 2/9 = 6/
- 1/25 = /625
-
Answer
17.
a. 12:4
b. 2.5:3
c. 19.5:9
d. 6/27
e. 25/625
How to reach the answer
a) Convert ratios to fractions 3:1 = ?:4
Cross multiply to find the missing value 3 x 4 = 1 x ?
Solve 12 = ?
How to reach the answer
5:6 = ?:3
b) Convert ratios to fractions 5/6 = ?/3
Cross multiply to find the missing value 5 x 3 = 6 x ?
Divide both sides to isolate the missing values (5 x 3)/6 = (6 x ?)/6
Solve 15/6 = ?
2.5 = ?
How to reach the answer
6.5:3 = ?:9
c) Convert 6.5/3 = ?/9
Cross multiply 6.5 x 9 = 3 x ?
Divide (6.5 x 9)/3 = (3 x ?)/3
Solve 19.5 = ?
How to reach the answer
2/9 = 6/?
d) Cross multiply 2 x ? = 6 x 9
Divide (2 x ?)/2 = (6 x 9)/2
Solve ? = 27
How to reach the answer
1/25 = ?/625
e) Cross multiply 1 x 625 = 25 x ?
Divide (1 x 625)/25 = (25 x ?)/25
Solve 25 = ?
18. Consider the list of 9 lengths of pipe below to answer the questions that follow.
8 cm, 15 cm, 3 cm, 8 cm, 80 cm, 12 cm, 8 cm, 25 cm and 15 cm
- List the lengths of pipe in order from shortest to longest.
- What is the middle (median) length of pipe?
- What is the most common (mode) length of pipe?
- What is the average (mean) of all the lengths of pipe?
- How would the mean length of pipe be affected if the longest length were removed from the list of pipe lengths?
-
Answer
a. 3 cm, 8 cm, 8 cm, 8 cm, 12 cm, 15 cm, 15 cm, 25 cm, 80 cm
b. Median = 12 cm
The median is the middle number in any data set. To determine the median, place measurements in order from highest to lowest. Since there are 9 measurements in this data set, the middle number is the fifth measurement. In this list the 5th measure is 12 cm.
c. Mode = 8 cm
The most common (or mode) of the data is the number that occurs the most often. In this list the most common number is 8 cm so this is the mode.
d. Mean (average) = 19.33 cm
The mean or average of a data set is calculated by adding up all the numbers and dividing by the amount of numbers in the data set.
average = 8 cm + 15 cm + 3 cm + 8 cm + 80 cm + 12 cm + 8 cm + 25 cm + 15 cm / 9 = 19.33 cm
e. The mean would decrease.
If the longest length of pipe were removed the average length would decrease. This can be proven with the same calculation as in (d).
average = (8 cm + 15 cm + 3 cm + 8 cm + 12 cm + 8 cm + 25 cm + 15 cm)/8 = 11.75 cm
If you remove a number that is higher than the mean, the mean will decrease and if you remove a number that is below the mean, the mean will increase.
Writing
Communicating by arranging words, numbers and symbols on paper or computer screen.
Filling in documents
Fill in the Incident Report Form on the following page using the information in the note below.
Date: January 27
My name is Pat King and I’m a prep cook in the hotel kitchen. Yesterday, I was working the early morning shift by myself. My job was to deep-fry the potatoes to get them ready for the breakfast rush. It was just after 7:00 am and I was running a little late. I went to take the last batch out of the deep fryer and when I shook the wire basket, my hand slipped and landed in the hot oil. I started yelling and shaking my hand to get the oil off but then the oil hit the flames on one of the burners and started a fire. The heat sensor on the exhaust hood must not have been working, because the fire damper didn’t come on. The fire kept getting bigger and I couldn’t reach the fire extinguisher. I kept yelling for help. Finally, one of the cleaning staff came, grabbed the fire extinguisher and put out the fire. He also called 9-1-1. Luckily, the fire only damaged the stove top and the exhaust hood is all black. When my supervisor came in, I told her everything that happened. Then the emergency workers came and gave me first aid for a minor burn. I took the rest of the day off and I’m not scheduled again until next week.
Incident report form
Name of worker:
Position: Department:
Location of incident:
Date of incident: Time: AM PM
Type of incident: Near miss? Minor injury? Serious injury?Reported to:
Nature of injury (if any):
Witnesses:
Damage to equipment or property:
Description of incident:
Signature: Date:
-
Answer
Incident report form
Name of worker: Pat King
Position: Prep Cook Department: Kitchen
Location of incident: Hotel Kitchen
Date of incident: January 27 Time: 7:00 am pm
Type of incident: Near miss? Minor injury? Serious injury?
Reported to: (Kitchen) supervisor
Nature of injury (if any): Hot oil burn to skin on worker's hand
Witnesses: Hotel cleaning staff saw the fire but not accident
Damage to equipment or property: Fire (smoke) damage to the stove top and exhaust hood
Description of incident:(Answers can vary, but they should follow this order.)
I was deep frying potatoes and my hand slipped and landed in the hot oil. The oil from my hand touched the flames on the burner and started a fire. The cleaner put the fire out with the fire extinguisher. The cleaner called 911. I reported the accident to my supervisor. The emergency workers came and gave me first aid.Signature: Date:
Putting it all together
Many tasks will require you to use more than one Essential Skill. For example, to complete the following time sheet you will need to read instructions, locate and use information in a list, make mathematical calculations, fill in numbers in a table and write a short note providing an explanation.
Complete the following questions using this timesheet information for the period January 12 to January 18:
- Your Employee Number is 1235 and you work in Department 299.
- Your regular work hours are 40 hours per week, 8:00 am to 4:30 pm, Monday to Friday, with 1/2 hour unpaid lunch.
- Your overtime is paid after 8 hours per day; overtime is also paid on weekends and holidays.
- Your rate of pay $15.00 per hour.
- Your overtime rate of pay is $22.00 per hour and you get a paid lunch on Saturdays and Sundays.
- Your hours worked for the week of January 12 to 18 are:
- Monday 8:00 am - 4:30 pm
- Tuesday 8:00 am - 6:00 pm
- Wednesday 8:00 am - 4:30 pm
- Thursday 8:00 am - 6:00 pm
- Friday 8:00 am - 4:30 pm
- Saturday 11:00 am - 5:00 pm
1. Complete this employee time sheet using the information provided on the previous page.
| Employee name: | ||||
|---|---|---|---|---|
| Employee number: | ||||
| Department: | ||||
| Date | Start time | End time | Regular hours | Overtime hours |
| Monday, January 12 | 8:00 am | 4:30 pm | 8 | n/a |
| Weekly totals | ||||
2. You need to make a request for time off for a medical reason. You will be having surgery on your knee and need to be off work from April 21 to April 28. Write your request here.
3. You will need to keep track of what you earn and check it against your pay stub. Calculate your gross pay (in other words before deductions) for this week.
-
Answer
1Employee time sheet Employee name: Employee number: 1235 Department: 299 Date Start time End time Regular hours Overtime hours Monday, January 12 8:00 am
4:30 pm
8
n/a
Tuesday, January 13 8:00 am
6:00 pm
8
1.5
Wednesday, January 14 8:00 am
4:30 pm
8
n/a
Thursday, January 15 8:00 am
6:00 pm
8
1.5
Friday, January 16 8:00 am
4:30 pm
8
n/a
Saturday, January 17 11:00 am
5:00 pm
0
6.0
Weekly totals
40
9
2. I am requesting time off for a medical reason. I will need to be off work from April 21 to April 28.
3. Gross pay = $798.00
How to reach the answer
40 regular hours x $15.00 = $600.00
9 hours of overtime x $22.00 = $198.00
$600 + $198 = $798
The gross (total) pay is $798.
Formula and conversion sheet
Basic conversions:
- 1 tsp = 5 mL
- 1 Tbsp. = 15 mL
- 1 cup = 250 mL
- 1 fluid cup = 8 fluid ounces
- 2.54 cm = 1 inch
- 12 inches = 1 foot
- 3 feet = 1 yard
- 1 yd2 = 9 sq. ft.
- 1 yd3 = 27 sq. ft.
Trigonometry
Pythagorean Theorem
a2 + b2 = c2
Description:
The Pythagorean theorem is: a squared plus b squared equals c squared
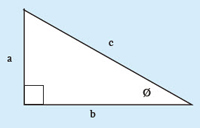
Description:
A right-angled triangle where the hypotenuse is side c. One of the angles is marked with the symbol for theta
sin Ø = opp/hyp
Description:
The sine (pronounced: sign) of theta equals opposite over hypotenuse.
cos Ø = adj/hyp
Description:
The cosine (pronounced co-sign) of theta equals adjacent over hypotenuse.
tan Ø = opp/adj
Description:
The tan of theta equals opposite over adjacent geometry formulas: pi equals 3.14.
Geometry formulas

Description:
pi? equals 3.14
- Circumference of a circle equals 2 pi times radius.
- Area of a circle equals pi times radius squared.
- A diagram of a circle with one line from the centre to one edge indicating radius. Radius is half the diameter of a circle.
- A diagram of a cylinder where radius and height are indicated.
- Volume of a cylinder equals pi times radius squared times height.
- Area equals length times width.
- A diagram of a rectangle where length and width are indicated.
- Volume of a rectangular prism equals length times width times height.
- A diagram of a rectangular prism where length, width and height are all indicated.
- Perimeter equals 2 times length plus width.
- A diagram of a rectangle where length and width are indicated.