Méthode d’essai biologique servant à mesurer des plantes terrestres exposées à des contaminants dans le sol : annexe I
Annexe I - Instructions pour la détermination des CIp à l’aide des analyses de régression linéaire et non linéaire
I.1 Introduction
La présente annexe fournit des instructions au sujet de l'utilisation des analyses de régression linéaire et non linéaire pour déterminer, à partir des relations concentration-réponse relatives aux paramètres quantitatifs (dans le cas présent, la longueur et la masse sèche moyennes des pousses et des racines), les CIp les plus pertinentes. La démarche proposée est une adaptation de celle décrite par Stephenson et coll. (2000b). Les instructions s'appuient sur la version 11.0 du logiciel SYSTATFootnote75; cependant, on peut utiliser n'importe quel logiciel approprié. Les techniques de régression décrites ici s'appliquent plus particulièrement à des données continues obtenues dans des essais comportant au moins dix concentrations ou catégories de traitements (y compris le traitement témoin négatif). Le plan d'expérience pour la mesure des effets d'une exposition prolongée sur diverses espèces de plantes est résumé au tableau I.1.
Un logigramme du processus général de sélection du modèle de régression le plus approprié pour chaque ensemble de données considéré est présenté à la figure 3 dans le corps du texte (v. 4.8.3.1).
Le lecteur est encouragé à consulter les sections appropriées du présent document, de même que les sections consacrées aux analyses de régression dans le document d'orientation d'Environnement Canada sur les méthodes statistiques applicables aux essais écotoxicologiques (EC, 2004a), avant d'entreprendre l'analyse des données. Ce même document contient également plusieurs références additionnelles relatives à l'analyse statistique de données d'essai quantitatives à l'aide de techniques de régression linéaire et non linéaire. Certains conseils contenus dans ces documents ont été incorporés dans la présente annexe, s'il y avait lieu.
| Paramètre | Description |
|---|---|
| Type d'essai | essai de toxicité sur un sol entier; sans renouvellement |
| Durée de l'essai | 14 jours pour le blé dur, le concombre, la laitue, l'orge, le radis, la tomate et le trèfle violet; 21 jours pour l'agropyre du Nord, le boutelou gracieux, la carotte, la fétuque rouge et la luzerne |
| Espèces d'essai | monocotylédones :agropyre du Nord (Elymus lanceolatus; anciennement Agropyron dasystachyum), blé dur (Triticum durum), boutelou gracieux (Bouteloua gracilis), fétuque rouge (Festuca rubra), orge (Hordeum vulgare); dicotylédones : carotte (Daucus carota), concombre (Cucumis sativus), laitue (Lactuca sativa), luzerne (Medicago sativa), radis(Raphanus sativus), tomate (Lycopersicon esculentum), trèfle violet (Trifolium pratense) |
| Nombre de répétitions | ≥4 répétitions par traitement pour un essai avec des répétitions identiques; pour un essai avec un nombre de répétitions variable selon les traitements :
|
| Nombre de traitements | sol témoin négatif et ≥9 concentrations d'essai; cependant, il est fortement recommandé d'utiliser ≥11 concentrations plus un sol témoin négatif |
| Paramètres statistiques | quantiques :
|
| Paramètres statistiques | quantitatifs :
|
I.2 Analyses de régression linéaire et non linéaire
I.2.1 Création de tableaux de données
Nota : L'analyse statistique doit comprendre la transformation logarithmique des concentrations (p. ex. log10 ou loge). Si les concentrations sont inférieures à 1 (p. ex. 0,25), on peut transformer les données en changeant d'unité (p. ex. en passant de mg/kg à µg/g) à l'aide d'un facteur de multiplication (p. ex. 1 000); les données modifiées sont ensuite soumises à une transformation logarithmique. La transformation peut être effectuée soit dans la feuille de calcul électronique initiale, soit au moment où les données initiales sont transférées dans le fichier de données SYSTAT.
- Ouvrir le fichier approprié contenant l'ensemble de données dans une feuille de calcul électronique.
- Lancer le programme SYSTAT. Dans l'écran principal, choisir File, New puis Data. Un tableau de données vide apparaît alors à l'écran. Saisir les noms des variables dans les en-têtes de colonne en double-cliquant sur un nom de variable, ce qui ouvre la fenêtre « Variable Properties ». Saisir un nom approprié pour la variable d'intérêt dans la boîte « Variable Name » et choisir le type de variable; des commentaires additionnels peuvent être saisis dans la boîte « Comments ». Par exemple, les noms de variable suivants pourraient être utilisés :
conc = concentration ou catégorie de traitement
logconc = transformation logarithmique (log10) de la concentration ou de la catégorie de traitement
rep = répétition pour une catégorie de traitement donnée
mnlengths = longueur moyenne des pousses
mnlengthr = longueur moyenne des racines
drywts = masse sèche des pousses
drywtr = masse sèche des racines - Les données peuvent maintenant être transférées. Pour transférer les données, copier et coller chaque colonne de la feuille de calcul électronique contenant les concentrations, les répétitions et les valeurs moyennes associées dans le tableau de données SYSTAT.
- Sauvegarder les données en cliquant sur File, puis sur Save As; une fenêtre « Save As » apparaît. Utiliser un code approprié pour sauvegarder le fichier de données. Cliquer sur Save lorsque le nom du fichier a été saisi.
- Consigner le nom du fichier de données SYSTAT sur la feuille de calcul contenant les données initiales.
- Si les données (concentrations d'essai) exigent une transformation, on peut effectuer la transformation en choisissant Data, Transform, puis Let.... Une fois dans la fonction Let..., choisir l'en-tête de colonne approprié pour les données transformées (p. ex. logconc), puis Variable dans la boîte « Add to » pour saisir la variable dans la boîte « Variable: ». Choisir la transformation appropriée (p. ex. L10 pour la transformation en log10 ou LOG pour le logarithme naturel) dans la boîte « Functions: » (la boîte « Function Type: » devrait afficher Mathematical), puis Add pour saisir la fonction dans la boîte « Expression: ». Choisir l'en-tête de colonne contenant les données initiales non transformées (p. ex. « conc » pour concentration ou catégorie de traitement), puis Expression dans la boîte « Add to » pour saisir la variable dans la boîte « Expression: ». S'il faut appliquer un facteur de multiplication pour ajuster la concentration avant la transformation logarithmique, on peut le faire dans la boîte « Expression: » (p. ex. L10[conc*1000]). Cliquer sur OK lorsque toutes les transformations sont terminées. Les données transformées apparaîtront dans la colonne appropriée. Sauvegarder les données (cliquer sur File, puis sur Save).
Nota : Il n'est pas possible de déterminer le log10 du traitement témoin négatif (le log10 de zéro n'est pas défini); par conséquent, il faut affecter au traitement témoin négatif une concentration très faible (p. ex. 0,001) dont on sait ou présume qu'elle est sans effet, afin d'inclure ce traitement dans l'analyse et de le distinguer des autres concentrations transformées. - À partir du tableau de données, calculer et consigner la moyenne des témoins négatifs pour la variable étudiée; chaque paramètre de mesure est soumis à une analyse statistique indépendante. La valeur moyenne de ces données témoins sera requise au moment de l'estimation des paramètres du modèle. Déterminer en outre la valeur maximale de cette variable particulière dans l'ensemble de données et l'arrondir au nombre entier le plus proche. Ce nombre correspondra à la valeur maximale sur l'axe des y (« ymax ») au moment de la création d'un graphique des données de régression.
I.2.2 Création d'un diagramme de dispersion ou d'un graphique linéaire
Les diagrammes de dispersion et les graphiques linéaires fournissent une indication de la forme de la courbe concentration-réponse pour l'ensemble de données. On peut alors comparer la forme de cette courbe avec chaque modèle (figure I.1) afin de choisir le ou les modèles susceptibles de convenir le mieux aux données. Chacun des modèles choisis devrait être utilisé pour analyser les données. Ensuite, après examen, le modèle présentant le meilleur ajustement est retenu.
- Choisir Graph, Summary Charts, puis Line.... Choisir la variable indépendante (p. ex. logconc) et cliquer sur Addpour saisir la variable dans la boîte « X-variable(s): ». Choisir la variable dépendante étudiée et cliquer sur Add pour saisir la variable dans la boîte « Y-variable(s): ». Cliquer sur OK. Un graphique s'affiche sous l'onglet « Output Pane » de l'écran principal SYSTAT, contenant les valeurs moyennes pour chaque catégorie de traitement; pour agrandir le graphique, cliquer simplement sur l'onglet « Graph Editor » situé sous la fenêtre centrale. On peut également visualiser un diagramme de dispersion des données en cliquant sur Graph, Plots, puis Scatterplot... et en suivant les instructions fournies pour saisir les variables x et y. Les graphiques fournissent une indication de la tendance générale de la relation concentration-réponse et permettent de choisir le ou les modèles susceptibles de présenter le meilleur ajustement, en plus d'une valeur estimative de la CIpd'intérêt.
Nota : L'écran principal SYSTAT est divisé en trois parties. La partie gauche de l'écran (onglet « Output Organizer ») fournit une liste de toutes les fonctions exécutées (p. ex. graphiques) - pour visualiser chaque fonction, il suffit de cliquer sur l'icône désirée. La partie droite de l'écran constitue la fenêtre centrale dans laquelle les résultats généraux de toutes les fonctions exécutées (p. ex. régression, graphiques) peuvent être visualisés. Les onglets situés sous cette fenêtre centrale permettent à l'utilisateur de basculer entre les fichiers de données (« Data Editor »), les graphiques individuels (« Graph Editor ») et les résultats (« Output Pane »). On peut visualiser individuellement les divers graphiques produits sous l'onglet « Graph Editor » en choisissant le graphique d'intérêt dans la partie gauche de l'écran (onglet « Output Organizer »). Dans la partie inférieure de l'écran sont affichés les codes de commande utilisés pour obtenir les fonctions désirées (p. ex. codes de régression et de graphique). L'onglet « Log » de cet écran de commande permet d'afficher une récapitulation de toutes les fonctions qui ont été exécutées. - Estimer visuellement et consigner une valeur estimative de la CIp d'intérêt (p. ex. CI25) pour l'ensemble de données. Par exemple, pour une CI25, diviser la moyenne des témoins par quatre et repérer cette valeur sur l'axe des y. Tracer une ligne horizontale à partir du point correspondant sur l'axe des y jusqu'à son intersection avec les points de données. À partir de ce point d'intersection, tracer une ligne verticale jusqu'à l'axe des x et consigner la valeur de la concentration obtenue (valeur estimative de la CI25).
- À partir des diagrammes de dispersion ou des graphiques linéaires, choisir le ou les modèles susceptibles de décrire le mieux la tendance concentration-réponse (un exemple de chaque modèle est présenté à la figure I.1).
Modèle exponentiel
CI50 : mnlengths = a*exp(log((a-a*0.5-b*0.5)/a)*(logconc/x))+b
CI25 : mnlengths = a*exp(log((a-a*0.25-b*0.75)/a)*(logconc/x))+b
où :
a = ordonnée à l'origine (réponse dans le témoin)
x = CIp pour l'ensemble de données
b = paramètre d'échelle (estimé entre 1 et 4)

Modèle de Gompertz
CI50 : mnlengths = g*exp((log(0.5))*(logconc/x)^b)
CI25 : mnlengths = g*exp((log(0.75))*(logconc/x)^b)
où :
g = ordonnée à l'origine (réponse dans le témoin)
x = CIp pour l'ensemble de données
logconc = valeur logarithmique de la concentration d'exposition
b = paramètre d'échelle (estimé entre 1 et 4)

Modèle d'hormèse
CI50 : mnlengthr = (t*(1+h*logconc))/(1+((0.5+h*logconc)/0.5)*(logconc/x)^b)
CI25 : mnlengthr = (t*(1+h*logconc))/(1+((0.25+h*logconc)/0.75)*(logconc/x)^b)
où :
t = ordonnée à l'origine (réponse dans le témoin)
h = effet hormétique (estimé entre 0,1 et 1)
x = CIp pour l'ensemble de données
logconc = valeur logarithmique de la concentration d'exposition
b = paramètre d'échelle (estimé entre 1 et 4)


Modèle linéaire
CI50 : drywtr = ((-b*0.5)/x)*logconc+b
CI25 : drywtr = ((-b*0.25)/x)*logconc+b
où :
b = ordonnée à l'origine (réponse dans le témoin)
x = CIp pour l'ensemble de données
logconc = valeur logarithmique de la concentration d'exposition
Modèle logistique
CI50 : drywts = t/(1+(logconc/x)^b)
CI25 : drywts = t/(1+(0.25/0.75)*(logconc/x)^b)
où :
t = ordonnée à l'origine (réponse dans le témoin)
x = CIp pour l'ensemble de données
logconc = valeur logarithmique de la concentration d'exposition
b = paramètre d'échelle (estimé entre 1 et 4)

Figure I.1
- Équations de la version 11.0 du logiciel SYSTAT pour les modèles de régression linéaire et non linéaire et exemples de graphiques des tendances observées pour chaque modèle « mnlengths » et « mnlengthr » désignent respectivement les longueurs moyennes des pousses et des racines, et « drywts » et « drywtr », respectivement les masses sèches moyennes des pousses et des racines individuelles
- Estimer visuellement et consigner une valeur estimative de la CIp d'intérêt (p. ex. CI25) pour l'ensemble de données. Par exemple, pour une CI25, diviser la moyenne des témoins par quatre et repérer cette valeur sur l'axe des y. Tracer une ligne horizontale à partir du point correspondant sur l'axe des y jusqu'à son intersection avec les points de données. À partir de ce point d'intersection, tracer une ligne verticale jusqu'à l'axe des x et consigner la valeur de la concentration obtenue (valeur estimative de la CI25).
- À partir des diagrammes de dispersion ou des graphiques linéaires, choisir le ou les modèles susceptibles de décrire le mieux la tendance concentration-réponse (un exemple de chaque modèle est présenté à la figure I.1).
I.2.3 Estimation des paramètres du modèle
- Choisir File, Open, puis Command.
- Ouvrir le fichier contenant les codes de commande pour le modèle particulier choisi à la section I.2.2 (choisir le fichier approprié et cliquer sur Open) :
nonline.syc = modèle exponentiel
nonling.syc = modèle de Gompertz
nonlinh.syc = modèle logistique avec effet d'hormèse
linear.syc = modèle linéaire
nonlinl.syc = modèle logistique
Le fichier fournit les codes de commande correspondant au modèle choisi sous l'onglet approprié de la boîte de l'éditeur de commandes au bas de l'écran principal. Tous les codes de commande pour déterminer les CI50 et les CI25 sont indiqués au tableau I.2; cependant, les équations peuvent être structurées de manière à permettre la détermination de n'importe quelle CIp. Par exemple, les codes de commande pour obtenir une CI25 à l'aide du modèle logistique seraient les suivants :
nonlin
print = long
model drywts = t/(1+(0.25/0.75)*(logconc/x)^b)
save resid1/ resid
estimate/ start = 85, 0.6, 2 iter = 200
use resid1
pplot residual
plot residual*logconc
plot residual*estimate - Taper l'en-tête de la colonne dans le tableau de données contenant la variable d'intérêt à analyser sur la ligne intitulée « model y= » (où « y » est la variable dépendante, p. ex. drywts).
- La quatrième ligne du texte devrait indiquer « save resida/ resid », où « a » représente un nombre affecté au fichier du résidu. Inscrire ce même nombre sur la sixième ligne (« use resida ») afin que le même fichier soit utilisé pour créer un diagramme de probabilité normale et des graphiques des résidus. Les lignes de commande qui suivent expliquent comment créer un diagramme de probabilité (« pplot residual »), un graphique des résidus en fonction de la concentration ou de la catégorie de traitement (« plot residual*logconc ») et un graphique des résidus en fonction des valeurs prévues et ajustées (« plot residual*estimate »). Ces graphiques facilitent l'évaluation des hypothèses de normalité (p. ex. diagramme de probabilité) et d'homogénéité des résidus (p. ex. graphiques des résidus) lorsqu'on détermine le modèle qui présente le meilleur ajustement (v. I.2.4).
- Inscrire la moyenne des témoins et la CIp estimative (p. ex. CI25) sur la cinquième ligne intitulée « estimate/start= » (des explications pour chaque modèle sont fournies au tableau I.2). Ces valeurs ont été déterminées initialement par examen du diagramme de dispersion ou du graphique linéaire. Une fois la convergence atteinte, le modèle fournit un ensemble de paramètres à partir duquel la CIp et ses limites de confiance à 95 % sont indiquées (paramètre « x »). Il est essentiel de fournir des valeurs estimatives précises pour chaque paramètre avant d'exécuter le modèle, sinon la méthode itérative utilisée pour déterminer les paramètres indiqués risque de ne pas converger. Le paramètre d'échelle (tableau I.2) est généralement estimé entre 1 et 4. Le nombre d'itérations peut varier, mais, dans le présent exemple, il a été fixé à 200 (« iter = 200 »). Habituellement, 200 itérations suffisent pour qu'il y ait convergence; si un plus grand nombre d'itérations s'avère nécessaire, cela signifie que le modèle employé n'est pas celui qui convient le mieux.
- Choisir File, puis Submit Window pour exécuter les commandes; ou bien, cliquer sur Submit Window avec le bouton droit de la souris. On obtient ainsi une sortie imprimée des itérations contenant les paramètres estimés et une liste des points de données réels avec les valeurs prévues et les résidus correspondants. Un graphique préliminaire de la courbe de régression est également présenté, mais ce graphique devrait être supprimé. Pour supprimer le graphique, cliquer sur le graphique apparaissant dans la fenêtre gauche de l'écran principal. Un diagramme de probabilité normale et des graphiques des résidus seront également présentés.
| Modèle | Codes de commande | |
|---|---|---|
| Exponentiel | nonlin print = long model mnlengths = a*exp(log((a-a*0.25-b*0.75)/a)*(logconc/x))+b save resid1/ resid estimate/ start = 25a, 1b, 0.3citer = 200 use resid1 pplot residual plot residual*logconc plot residual*estimate |
où : a Représente la valeur estimative de l'ordonnée à l'origine (« a ») (réponse dans le témoin) b Représente le paramètre d'échelle (« b ») (estimé entre 1 et 4) c Représente la valeur estimative de la CIp pour l'ensemble de données (« x ») |
| Gompertz | nonlin print = long model mnlengths = g*exp((log(0.75))*(logconc/x)^b) save resid2/ resid estimate/ start = 16a, 0.8b, 1citer = 200 use resid2 pplot residual plot residual*logconc plot residual*estimate |
où : a Représente la valeur estimative de l'ordonnée à l'origine (« g ») (réponse dans le témoin) b Représente la valeur estimative de la CIp pour l'ensemble de données (« x ») c Représente le paramètre d'échelle (« b ») (estimé entre 1 et 4) |
| Hormèse | nonlin print = long model mnlengthr = (t*(1+h*logconc))/(1+((0.25+h*logconc )/ 0.75)*(logconc/x)^b) save resid3/ resid estimate/start = 48a, 0.1b, 0.7c, 1d iter = 200 use resid3 pplot residual plot residual*logconc plot residual*estimate |
où : a Représente la valeur estimative de l'ordonnée à l'origine (« t ») (réponse dans le témoin) b Représente l'effet hormétique (« h ») (estimé entre 0,1 et 1) c Représente la valeur estimative de la CIppour l'ensemble de données (« x ») d Représente le paramètre d'échelle (« b ») (estimé entre 1 et 4) |
| Linéaire | nonlin print = long model drywtr = ((-b*0.25)/x)*logconc+b save resid4/ resid estimate/start = 5a, 0.7b iter = 200 use resid4 pplot residual plot residual*logconc plot residual*estimate |
où : a Représente la valeur estimative de l'ordonnée à l'origine (« b ») (réponse dans le témoin) b Représente la valeur estimative de la CIp pour l'ensemble de données (« x ») |
| Logistique | nonlin print = long model drywts = t/(1+(0.25/0.75)*(logconc/x)^b) save resid5/resid estimate/start = 85a, 0.6b, 2citer = 200 use resid5 pplot residual plot residual*logconc plot residual*estimate |
où : a Représente la valeur estimative de l'ordonnée à l'origine (« t ») (réponse dans le témoin) b Représente la valeur estimative de la CIppour l'ensemble de données (« x ») c Représente le paramètre d'échelle (« b ») (estimé entre 1 et 4) |
Nota : « mnlengths » et « mnlengthr » désignent respectivement les longueurs moyennes des pousses et des racines, « drywts » et « drywtr », respectivement les masses sèches moyennes des pousses et des racines individuelles et « pplot », la création d'un diagramme de probabilité fondé sur les résidus obtenus à partir du modèle de régression étudié.
I.2.4 Examen des résidus et des hypothèses de l'essai
Un examen des résidus obtenus avec chaque modèle mis à l'essai aide à déterminer si les hypothèses de normalité et d'homoscédasticité ont été satisfaites. Si l'une ou l'autre des hypothèses n'a pas pu être satisfaite, quel que soit le modèle examiné, il est conseillé de demander conseil à un statisticien avant d'examiner d'autre modèles ou bien d'analyser une nouvelle fois les données à l'aide de la méthode d'interpolation linéaire (en faisant appel au programme ICPIN; v. 4.8.3.2), qui est moins souhaitable.
I.2.4.1 Hypothèse de normalité.
Pour vérifier la normalité, il convient d'utiliser le test de Shapiro-Wilk comme il est expliqué dans EC (2004a); des instructions au sujet de l'exécution de ce test sont données en I.2.4.3. On peut également se servir du diagramme de probabilité normale, affiché sous l'onglet « Output Pane », pour déterminer si l'hypothèse de normalité est satisfaite. Les résidus devraient former une ligne relativement droite qui traverse le graphique en diagonale; une ligne courbe signifie un écart avec la normalité. Cela dit, le diagramme de probabilité normale ne devrait pas constituer le seul test de normalité, car pour déterminer si un graphique est « normal » (ligne droite) ou « non normal » (ligne courbe), l'analyste fait appel à une évaluation subjective. Si les données ne sont pas distribuées normalement, il est conseillé d'utiliser un autre modèle, de demander l'avis d'un statisticien ou bien d'analyser les données à l'aide de la méthode d'interpolation linéaire, qui est moins souhaitable.
I.2.4.2 Homogénéité des résidus.
L'homoscédasticité (ou homogénéité) des résidus devrait être évaluée à l'aide du test de Levene, comme il est expliqué dans EC (2004a) (des instructions pour l'exécution de ce test sont données en I.2.4.3), et en examinant les graphiques des résidus en fonction des valeurs réelles et prévues (estimées). L'homogénéité des résidus se traduit par une distribution égale de la variance des résidus en regard de la variable indépendante (concentration ou catégorie de traitement) (figure I.2A). Le test de Levene, s'il est significatif, indiquera que les données ne sont pas homogènes. Si les données (selon le test de Levene) présentent une hétéroscédasticité (c.-à-d. si elles ne sont pas homogènes), il convient d'examiner les graphiques des résidus. Si l'on observe un changement important dans la variance et si les graphiques des résidus sont incontestablement en forme d'éventail ou de « V » (on trouvera un exemple de graphique de « residual*estimate » à la figure I.2B; on observe également une forme en « V » dans le sens opposé dans le graphique de « residual*logconc»), il est recommandé de répéter l'analyse des données à l'aide de la méthode de régression pondérée. Par contre, si l'on observe une divergence, probablement due à un défaut systématique d'ajustement (figure I.2C), cela signifie que le modèle choisi ne convient pas ou qu'il est incorrect.
I.2.4.3 Évaluation des hypothèses de normalité et d'homogénéité des résidus.
La version 11.0 de SYSTAT permet d'effectuer à la fois le test de Shapiro-Wilk et celui de Levene pour évaluer les hypothèses de normalité et d'homogénéité des résidus. Le test de Levene ne peut être effectué que par le biais d'une analyse de la variance (ANOVA) sur les valeurs absolues des résidus obtenus en I.2.3.
- Choisir File, Open, puis Data pour ouvrir le fichier de données contenant les résidus créés en I.2.3 (p. ex. resid1.syd).
- Saisir un nouveau nom de variable dans une colonne vide en double-cliquant sur le nom de la variable, ce qui ouvre la fenêtre « Variable Properties ». Dans cette fenêtre, saisir un nom approprié pour les résidus transformés (p. ex. absresiduals) dans la boîte « Variable name: ». Transformer les résidus en choisissant Data, Transform, puis Let.... Une fois dans la fonction Let..., choisir l'en-tête de la colonne contenant le titre approprié pour les données transformées (p. ex. absresiduals), puis choisir Variable dans la boîte « Add to » pour saisir la variable dans la boîte « Variable: ». Choisir la transformation appropriée (p. ex. ABS pour transformer les données en leurs valeurs absolues) dans la boîte « Functions: » (la boîte « Function Type: » devrait indiquer Mathematical), puis cliquer sur Add pour saisir la fonction dans la boîte « Expression: ». Choisir l'en-tête de colonne contenant les données initiales non transformées (résidus), puis Expression dans la boîte « Add to » afin de saisir la variable dans la boîte « Expression: ». Cliquer sur OK; les données transformées apparaîtront dans la colonne appropriée. Sauvegarder les données.
- Pour effectuer le test de Shapiro-Wilk, choisir Analysis, Descriptive Statistics, puis Basic Statistics.... Une fenêtre « Column Statistics » apparaîtra. Choisir les résidus dans la boîte « Available variable(s): », puis cliquer sur Addpour saisir cette variable dans la boîte « Selected variable(s): ». Dans la boîte « Options », cliquer sur Shapiro-Wilk normality test, puis sur OK. Un petit tableau apparaîtra dans la fenêtre « Output Organizer » de SYSTAT, où la valeur critique de Shapiro-Wilk (« SW Statistic ») et la valeur de la probabilité (« SW P-Value ») seront affichées. Une probabilité supérieure au critère habituel (p > 0,05) indique que les données sont distribuées normalement.
- Pour effectuer le test de Levene, choisir Analysis, Analysis of Variance(ANOVA), puis Estimate Model...; une fenêtre intitulée « Analysis of Variance:Estimate Model » apparaîtra.
- Choisir la variable sous laquelle les données doivent être groupées (p. ex. logconc), et saisir cette variable dans la boîte « Factor(s): » en cliquant sur Add.
- Choisir les résidus transformés (absresiduals), puis cliquer sur Add pour saisir la variable dans la boîte « Dependent(s): ». Cliquer sur OK. Un graphique des données et une sortie imprimée des résultats apparaîtront sous l'onglet « Output Pane ». Une probabilité supérieure au critère habituel (p > 0,05) indique que les données sont homogènes.
I.2.5 Pondération des données
Si les résidus présentent une hétéroscédasticité (selon le test de Levene) et si l'on observe un changement important dans la variance entre les catégories de traitement (c.-à-d. si le graphique est incontestablement en forme d'éventail oude « V »; v. figure I.2B), il est recommandé de procéder à une nouvelle analyse à l'aide d'une régression pondérée. Dans une régression pondérée, on utilise l'inverse de la variance des observations pour chaque concentration ou catégorie de traitement comme coefficients de pondération. Lorsqu'on exécute la régression pondérée, l'erreur type pour la CIp[présentée dans SYSTAT comme étant l'erreur type asymptotique (« A.S.E. »); v. figure I.3] est comparée à celle obtenue par la méthode de régression non pondérée. Si la différence entre les deux erreurs types est supérieure à 10 %, la régression pondérée est à privilégier. En revanche, si le changement dans la variance entre toutes les catégories de traitement est important, et si la différence entre les erreurs types est inférieure à 10 %**, il convient de demander l'avis d'un statisticien au sujet de l'utilisation d'autres modèles; on pourrait aussi analyser de nouveau les données par la méthode d'interpolation linéaire, qui est moins souhaitable. On procède à cette comparaison entre les régressions pondérée et non pondérée pour chacun des modèles retenus jusqu'au choix final du modèle (modèle et régression correspondant au meilleur choix). Par contre, si le test de Levene montre que les données ne sont pas homogènes et que les graphiques des résidus présentent une absence de divergence (v. figure I.2C), il est possible que le modèle choisi soit inapproprié ou incorrect. Il convient alors de demander l'avis d'un statisticien avant d'utiliser d'autres modèles.
**La valeur de 10 % est une règle empirique. Il existe des tests objectifs pour vérifier l'amélioration apportée par la pondération, mais ces tests dépassent la portée du présent document. La pondération ne devrait être utilisée qu'en cas de besoin, car la procédure peut introduire des complications supplémentaires dans la modélisation. Il est recommandé de demander l'avis d'un statisticien lorsque la pondération se révèle nécessaire, mais que les valeurs estimées des paramètres sont dénuées de sens.
Figure I.2. Graphique des résidus en fonction des valeurs prévues (estimées) (« residuals*estimate ») indiquant une homoscédasticité (A) et deux types d'hétéroscédasticité, l'un (B) avec une forme en éventail ou en « V » exigeant un examen plus approfondi à l'aide d'une régression pondérée et l'autre (C) qui met en évidence un défaut d'ajustement systématique résultant du choix d'un modèle incorrect



- Choisir File, Open, puis Data. Choisir le fichier contenant l’ensemble de données à pondérer. Saisir les deux nouveaux noms de variable dans l’en-tête de colonne en double-cliquant sur un nom de variable, ce qui ouvre la fenêtre « Variable Properties ». Dans cette fenêtre, saisir un nom approprié pour la variable d’intérêt, choisir le type de variable et inscrire des commentaires, le cas échéant. Les deux nouveaux en-têtes de colonne devraient indiquer la variance d’une variable donnée (p. ex. vardrywts), et l’inverse de la variance pour cette variable (p. ex. varinvsdrywts). Sauvegarder le fichier de données en cliquant sur File, puis sur Save.
- Choisir Data, puis By Groups.... Choisir la variable indépendante (logconc), puis cliquer sur Add afin de saisir cette variable dans la boîte « Selected variable(s): »; on pourra ainsi déterminer la variance de la variable d’intérêt par concentration ou catégorie de traitement (« group »). Cliquer sur OK.
- Choisir Analysis, Descriptive Statistics, puis Basic Statistics.... Choisir la variable d’intérêt à pondérer (p. ex. drywts), puis cliquer sur Add pour saisir cette variable dans la boîte « Selected variable(s): ». Choisir Variance dans la boîte « Options », puis cliquer sur OK. Cette fonction affichera la variance pour la variable d’intérêt, groupée par concentration ou catégorie de traitement, sous l’onglet « Output Pane » de l’écran principal.
- Choisir Data, By Groups..., puis cliquer sur la boîte située à côté de Turn off, et ensuite sur OK afin que toute analyse subséquente ne soit pas effectuée selon chaque concentration ou catégorie de traitement individuelle, mais qu’elle prenne en compte l’ensemble de données au complet.
- Revenir au fichier de données en choisissant l’onglet « Data Editor » sur l’écran principal. Transférer les variances correspondant à chaque concentration ou catégorie de traitement dans la colonne des variances (p. ex. vardrywts). On remarquera que la variance est la même pour les répétitions d’un même traitement.
- Choisir Data, Transform, puis Let.... Choisir ensuite l’en-tête de colonne contenant l’inverse de la variance (p. ex. varinvsdrywts) pour la variable d’intérêt, puis Variable dans la boîte « Add to » afin de saisir la variable dans la boîte « Variable: ». Choisir la boîte « Expression: » et taper « 1/ », puis l’en-tête de colonne contenant les variances (p. ex. vardrywts) de la variable d’intérêt pour chaque répétition et concentration, et ensuite Expression dans la boîte « Add to » afin de saisir la variable dans la boîte « Expression: ». Cliquer sur OK. L’inverse de la variance pour chaque répétition et concentration sera affiché dans la colonne appropriée. Sauvegarder les données en cliquant sur File, puis sur Save.
- Choisir File, Open, puis Command; ouvrir le fichier contenant les codes de commande pour estimer les paramètres de l’équation (v. I.2.3, étape 2) correspondant au modèle choisi pour l’analyse sans pondération.
- Insérer une ligne additionnelle après la troisième ligne en tapant « weight=varinvsy », où « y » est la variable dépendante à pondérer (p. ex. weight=varinvsdrywts), comme il est indiqué dans la ligne ombrée ci-dessous :
nonlin
print=long
model drywts = t/(1+(0.25/0.75)*(logconc/x)^b)
weight=varinvsdrywts
save resid2/ resid
estimate/ start = 85, 0.6, 2 iter=200
use resid2
pplot residual
plot residual*logconc
plot residual*estimate - Affecter un nouveau nombre aux résidus sur la ligne intitulée « save resida » (où « a » représente le nombre affecté).
Figure I.3 Exemple des données de sortie initiales obtenues à l’aide du modèle logistique de la version 11.0 de SYSTAT. Les données de sortie initiales comprennent l'erreur quadratique moyenne résiduelle utilisée pour choisir le meilleur modèle, de même que les CIp, l'erreur type pour la valeur estimative et les limites de confiance à 95 % inférieure et supérieure. Le nombre de cas affichés a été réduit aux fins de la présente figure; toutefois, SYSTAT affiche tous les cas, y compris la mesure réelle de la variable et la valeur estimative prévue et le résidu correspondants.
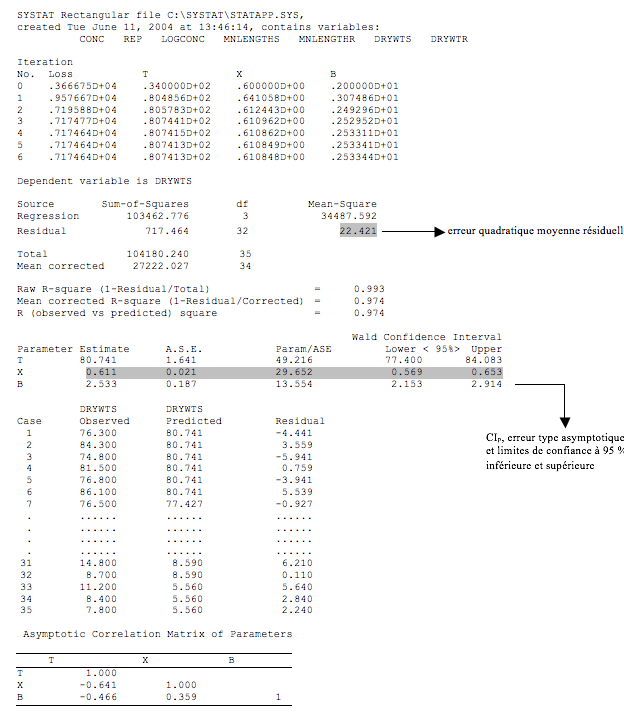
- Inscrire la moyenne des témoins et la CIp estimée sur la ligne intitulée « estimate/ start… » (des explications sont fournies au tableau I.2 pour chaque modèle). Ces valeurs estimatives seront les mêmes que celles utilisées pour l’analyse sans pondération.
- Choisir File, puis Submit Window pour exécuter les commandes. On obtient ainsi les résultats des itérations, les paramètres estimés et une liste des points de données avec les valeurs prévues et les résidus correspondants sous l’onglet « OutputPane » de l’écran principal. Un graphique préliminaire de la courbe de régression estimée est également présenté, mais ce graphique devrait être supprimé. Un diagramme de probabilité normale et des graphiques des résidus seront également présentés.
- Poursuivre l’analyse comme il est expliqué en I.2.4 afin de vérifier que toutes les hypothèses du modèle sont satisfaites.
- Comparer les résultats de l’analyse de régression pondérée et ceux de l’analyse sans pondération. Choisir la régression pondérée si la pondération réduit l’erreur type pour la CI Les données de sortie initiales comprennent l’erreur quadratique moyenne résiduelle utilisée pour choisir le meilleur modèle, de même que les CIp, l’erreur type pour la valeur estimative et les limites de confiance à 95 % inférieure et supérieure. Le nombre de cas affichés a été réduit aux fins de la présente figure; toutefois, SYSTAT affiche tous les cas, y compris la mesure réelle de la variable et la valeur estimative prévue et le résidu correspondants.
I.2.6 Présence de valeurs aberrantes et d’observations inhabituelles
Une valeur aberrante est révélatrice d’une mesure qui ne semble pas concorder avec les autres valeurs obtenues lors de l’essai. On peut détecter les valeurs aberrantes et les observations inhabituelles en examinant l’ajustement de la courbe concentration-réponse en regard de tous les points de données, de même que les graphiques des résidus. Si une valeur aberrante est détectée, il convient d’examiner avec soin les notes de l’essai (notes prises à la main, feuilles de données électroniques et conditions expérimentales) à la recherche d’une erreur humaine. Si la valeur aberrante est due à une erreur de transcription qui ne peut être corrigée ou à une erreur de procédure, le point de données correspondant devrait être exclu de l’analyse. Lorsqu’une valeur aberrante est détectée, il est recommandé de procéder à l’analyse avec et sans la valeur aberrante. Pour décider de conserver ou d’exclure la valeur aberrante, on devrait prendre en considération la variation biologique naturelle et les phénomènes biologiques susceptibles d’être à l’origine de l’apparente anomalie. Quelle que soit la décision prise au sujet de la valeur aberrante, l’analyse finale doit être accompagnée d’une description des données, des valeurs aberrantes et des analyses avec et sans les valeurs aberrantes, de même que des conclusions interprétatives. S’il y a plus d’une valeur aberrante, il est recommandé de réévaluer le modèle choisi pour déterminer s’il convient vraiment et d’envisager des modèles de remplacement. Pour de plus amples indications au sujet de la présence de valeurs aberrantes et d’observations inhabituelles, le lecteur est invité à consulter EC (2004).
Pour déterminer si l’ensemble de données comporte des valeurs aberrantes, on peut effectuer une analyse de la variance (ANOVA) à l’aide du logiciel SYSTAT. Toutefois, l’ANOVA suppose que les résidus sont distribués normalement et, partant, il est nécessaire de vérifier les hypothèses de normalité avant d’appliquer l’ANOVA pour détecter les valeurs aberrantes. On peut également établir la présence de valeurs aberrantes en examinant les graphiques des résidus.
- Effectuer une ANOVA comme il est expliqué en I.4 afin de détecter les valeurs aberrantes éventuelles. Toute valeur aberrante sera identifiée à l’aide d’un numéro de cas correspondant au numéro de ligne dans le fichier de données SYSTAT. Le programme se sert des résidus studentisés pour mettre en évidence la présence de valeurs aberrantes; des valeurs >3 indiquent une possibilité de valeurs aberrantes. Cette possibilité devrait être confirmée par un examen des graphiques des résidus.
- Si l’on décide d’exclure la ou les valeurs aberrantes, supprimer la valeur dans le tableau (fichier) de données initial et sauvegarder de nouveau le fichier sous un nouveau nom (cliquer sur File, puis sur Save As...). Par exemple, ajouter la lettre « o » [pour indiquer qu’une valeur aberrante (outlier) a été éliminée] à la fin du nom initial du fichier.
- Répéter l’analyse de régression sans la ou les valeurs aberrantes en utilisant le même modèle et les mêmes valeurs estimatives des paramètres que ceux employés dans l’analyse de régression effectuée avant l’élimination des valeurs aberrantes. On peut aussi faire appel à d’autres modèles si le modèle utilisé permet d’obtenir un meilleur ajustement et une erreur quadratique moyenne résiduelle moins importante. Si l’élimination de la ou des valeurs aberrantes n’entraîne pas de changement significatif dans l’erreur quadratique moyenne résiduelle et dans la CIp (y compris les limites de confiance correspondantes), l’analyste doit faire appel à son jugement professionnel et décider (de manière subjective) s’il convient d’inclure ou non la ou les valeurs aberrantes. Les raisons justifiant l’exclusion ou l’inclusion des valeurs aberrantes éventuelles doivent être consignées dans le rapport d’analyse final.
I.2.7 Choix du modèle le plus approprié
Une fois l’ajustement effectué avec tous les modèles envisagés, il convient d’évaluer chaque modèle au regard de la normalité de la distribution, de l’homogénéité des résidus et de l’erreur quadratique moyenne résiduelle. Le modèle qui satisfait à toutes les hypothèses et qui fournit la plus petite erreur quadratique moyenne résiduelle (v. figure I.3) constitue le modèle à privilégier. Cela dit, lorsque plusieurs modèles conduisent à la même erreur quadratique moyenne résiduelle et que tous les autres facteurs sont équivalents, il convient de choisir le modèle le plus simple. Si une régression pondérée a été effectuée, on devrait comparer les résultats des deux analyses, avec et sans pondération, et choisir la régression pondérée si la pondération réduit l’erreur type pour la CIp de plus de 10 %. L’erreur quadratique moyenne résiduelle est présentée sous l’onglet « Output Pane » immédiatement après les itérations et avant les valeurs estimatives des paramètres. Toutefois, si aucun des modèles ne permet un ajustement convenable, il est conseillé de demander l’avis d’un statisticien au sujet de l’utilisation de modèles additionnels, ou d’analyser de nouveau les données par la méthode d’interpolation linéaire, qui est moins souhaitable (v. 4.8.3.2).
Nota : Étant donné que les concentrations ou les catégories de traitement étaient exprimées sous forme de logarithmes dans les calculs, les CIp et leurs limites de confiance devraient être transformées en valeurs arithmétiques aux fins du rapport d’analyse.
I.2.8 Création de la courbe concentration-réponse
Une fois le modèle approprié choisi, il faut créer la courbe concentration-réponse correspondant à ce modèle.
- Dans la fenêtre de l’éditeur de commande, au bas de l’écran, copier l’équation du modèle (c’est-à-dire l’équation qui suit le signe « = » sur la troisième ligne des codes de commande indiqués au tableau I.2) à partir des codes de commande utilisés pour déterminer les valeurs estimatives correspondant au modèle choisi; l’équation devrait comporter les caractères alphabétiques initiaux (p. ex. t, b, h, etc.). On peut copier l’équation en la surlignant et en cliquant ensuite sur Edit, puis sur Copy (ou en cliquant sur Copy avec le bouton droit de la souris).
- Choisir File, Open, puis Command et ouvrir un fichier de commande graphique existant (n’importe quel fichier dont le nom se termine par « *.cmd ») comme dans l’exemple suivant (ou, au besoin, créer un nouveau fichier), en utilisant le modèle logistique. Le premier graphique (« plot ») est un diagramme de dispersion de la variable dépendante en fonction de la série de concentrations logarithmiques. Le second graphique (« fplot ») correspond à l’équation de régression, en surimposition sur le diagramme de dispersion.
graph
begin
plot drywts*logconc/ title = ‘Dry Mass of Barley Shoots’, xlab = ‘Log(mg boric acid/kg soil d.wt)’,
ylab = ‘Mass (mg)’,
xmax = 2, xmin = 0, ymax = 90, ymin = 0
fplot y = 80.741/(1+(0.25/0.75)*(logconc/0.611)^2.533); xmin = 0,
xmax = 2, xlab = ‘‘ ymin = 0, ylab = ‘‘, ymax = 90
end - Coller l’équation copiée à la place de l’équation préexistante (comme il est indiqué dans la zone ombrée ci-dessus) en surlignant l’équation précédente, puis choisir Edit, et ensuite Paste (ou cliquer sur Paste avec le bouton droit de la souris). Remplacer tous les caractères alphabétiques (p. ex. t, b, h, x, a, etc.) par les valeurs estimatives indiquées sous l’onglet « Output Pane » après l’application du modèle choisi.
- Saisir l’information correcte sur la ligne intitulée « plot y*logconc… », où « y » est la variable dépendante étudiée (p. ex. la masse sèche). Ajuster en conséquence les valeurs numériques de « xmax » (concentration logarithmique maximale utilisée) et de « ymax » (v. I.2.1, étape 7). Vérifier que toutes les entrées « xlab » et « ylab » (étiquettes des axes des x et des y) sont correctes, sinon apporter les corrections nécessaires. Vérifier que tous les guillemets et les virgules sont à leur place dans le programme de commande, comme il est indiqué dans l’exemple précédent; SYSTAT tient compte de la casse et des espaces.
Nota :
‘title’ correspond au titre du graphique
‘xlab’ correspond à l’étiquette de l’axe des x
‘xmin’ correspond à la valeur minimale requise sur l’axe des x
‘xmax’ correspond à la valeur maximale requise sur l’axe des x
‘ylab’ correspond à l’étiquette de l’axe des y
‘ymax’ correspond à la valeur maximale requise sur l’axe des y
‘ymin’ correspond à la valeur minimale requise sur l’axe des y
Les valeurs de « xmin », « xmax », « ymin» et « ymax » doivent être les mêmes sur les deux graphiques pour que la droite de régression se superpose exactement sur le diagramme de dispersion des données. Un exemple du graphique de régression final est donné à la figure I.1 pour chacun des cinq modèles proposés. - Choisir File, puis Save Aspour sauvegarder les codes de commande graphique dans un dossier de travail approprié, sous le même code que celui utilisé pour créer le fichier de données, avec une indication du modèle auquel correspond la régression. Cliquer sur Savepour sauvegarder le fichier.
- Choisir File, puis Submit Window pour exécuter les codes de commande. Un graphique de la régression, fondé sur les valeurs estimatives des paramètres correspondant au modèle choisi, apparaîtra.
I.3 Détermination de CIp additionnelles
Dans certains cas, il peut être souhaitable d’estimer la CIp correspondant à une autre valeur de « p » (en sus ou à la place de la CI25). Les modèles proposés par Stephenson et coll. (2000b) permettent de choisir et de déterminer n’importe quelle CIp. Les paragraphes ci-dessous expliquent comment déterminer une CI20, mais il est possible de modifier les modèles pour déterminer la CIp quelle que soit la valeur de « p ».
- Choisir File, Open, puis Command et ouvrir le fichier correspondant aux codes de commande utilisés pour obtenir les valeurs estimatives des paramètres (on trouvera les codes de commande correspondant à chaque modèle au tableau I.2). Changer l’équation du modèle afin de calculer la CIp voulue (p. ex. CI20) en modifiant les fractions utilisées dans chaque modèle. Par exemple, pour calculer une CI20 à l’aide du modèle logistique, l’équation qui s’écrivait « t/(1+(0.25/0.75)*(logconc/x)^b) » (pour le calcul d’une CI25) deviendrait « t/(1(0.20/0.80)*(logconc/x)^b) ».
- Une fois l’équation modifiée selon la CIp voulue, suivre les étapes décrites en I.2.3, en n’omettant pas d’inscrire la CIp estimée (p. ex. CI20) sur la cinquième ligne intitulée « estimate/ start= » (des explications pour chaque modèle sont fournies à la figure I.1). Ces valeurs ont été établies initialement à la suite d’un examen du diagramme de dispersion ou du graphique linéaire. Une fois la convergence atteinte, le modèle fournit un ensemble de paramètres à partir duquel la CIp et ses limites de confiance à 95 % correspondantes sont indiquées (paramètre « x »).
- Procéder à l’analyse comme il est expliqué dans les sections I.2.4 à I.2.8 ci-dessus.
I.4 Analyse de la variance (ANOVA
- Choisir File, Open, puis Data pour ouvrir le fichier de données contenant toutes les observations relatives à l’ensemble de données examiné.
- Choisir « Analysis», « Analysis of Variance (ANOVA) », puis « Estimate Model... ».
- Choisir la variable sous laquelle les données doivent être groupées (p. ex. logconc) et saisir cette variable dans la boîte « Factor(s): » en cliquant sur Add.
- Choisir la variable d’intérêt ( p. ex. drywts), puis cliquer sur Add pour saisir la variable dans la boîte « Dependent(s): ».
- Choisir la boîte située à côté de « Save » (en bas à gauche de la fenêtre intitulée « Analysis of Variance: Estimate Model ») et déplacer la flèche vers le bas pour cliquer sur Residuals/Data. Taper un nom de fichier approprié dans la boîte de texte vide adjacente pour sauvegarder les résidus (p. ex. anova1). Cliquer sur OK. Un graphique des données et les résultats apparaîtront sous l’onglet « Output Pane ». À ce moment-là, toute valeur aberrante, selon les résidus studentisés, sera également détectée (on trouvera des conseils sur l’évaluation des valeurs aberrantes en I.2.6).
- Évaluer les hypothèses de normalité et d’homogénéité des résidus selon les explications données en I.2.4 en utilisant le fichier de données créé pour sauvegarder les résidus et les données avant l’analyse de la variance (p. ex. anova1). Après l’évaluation de la normalité et de l’homogénéité des résidus à l’aide des tests de Shapiro-Wilk et de Levene, respectivement, on peut utiliser les codes suivants pour examiner les graphiques des résidus :
graph
use anova1
plot residual*logconc
plot residual*estimate