Cahier d’exercices de mathématiques pour les métiers
Sur cette page
- Introduction
- Principes mathématiques
- Section 1 : Mesures et calculs
- Section 2 : Calculs monétaires
- Section 3 : Calendriers des budgets et des opérations comptables
- Section 4 : Analyse de données
Formats substituts

Cahier d’exercices de mathématiques pour les métiers [PDF - 1,03 Mo]
Les formats en gros caractères, braille, MP3 (audio), texte électronique, et DAISY sont disponibles sur demande en commandant en ligne ou en composant le 1 800 O-Canada (1-800-622-6232). Si vous utilisez un téléscripteur (ATS), composez le 1-800-926-9105.
Introduction
L’exercice d’un métier exige que vous ayez des compétences marquées en calcul pour vous aider au travail. Le présent cahier d’exercices inclut des questions et du matériel d’apprentissage qui vous aideront :
- à en savoir plus sur les compétences en calcul requises pour travailler dans les métiers;
- à découvrir comment les compagnons et les compagnes utilisent le calcul à leur travail;
- à pratiquer vos compétences en calcul;
- à déterminer quelles compétences en calcul vous devriez améliorer.
Le cahier d’exercices est divisé en 4 sections, chacune traitant d’un type différent de compétences en calcul que les compagnons et les compagnes utilisent à leur travail.
-
Mesures et calculs :
Compétences utilisées pour mesurer et décrire le monde physique, par exemple pour prendre des mesures ou pour calculer des superficies et des volumes. -
Calculs monétaires :
Compétences utilisées pour donner ou recevoir de l’argent au travail, par exemple pour manipuler de l’argent comptant, pour faire la monnaie, pour préparer des factures ou pour faire des paiements. -
Calendriers des budgets et des opérations comptables :
Compétences utilisées pour gérer le temps et l’argent, par exemple pour planifier l’utilisation de votre temps et de votre argent et consigner la façon dont vous utilisez ce temps et cet argent, pour choisir les produits ou les services qui offrent le meilleur rapport qualité prix ou pour utiliser votre temps et votre argent judicieusement. -
Analyse de données :
Compétences utilisées pour résoudre des problèmes en analysant et en comparant des données numériques.
Un corrigé est donné à la fin du cahier d’exercices pour vous aider à valider vos réponses et à déterminer dans quels domaines vous devriez améliorer vos compétences.
Principes mathématiques
L’exercice d’un métier exige de pouvoir exécuter la totalité ou la plupart des tâches mathématiques qui figurent plus bas.
| Principes mathématiques | Exemples en milieu de travail | |
|---|---|---|
|
Nombres entiers par exemple : 3, 14 |
Lire et écrire, compter, arrondir, additionner ou soustraire, multiplier ou diviser des nombres entiers. |
|
|
Nombres entiers relatifs par exemple : -5, 0, 11 |
Lire et écrire, additionner ou soustraire, multiplier ou diviser des nombres entiers relatifs. |
|
|
Fractions par exemple : 1/8", 1/4" |
Lire et écrire, arrondir, additionner ou soustraire, multiplier ou diviser des fractions. Multiplier ou diviser par une fraction. |
|
|
Nombres décimaux par exemple : 8,50, 0,00375 |
Lire et écrire, arrondir, additionner ou soustraire, multiplier ou diviser des nombres décimaux. Multiplier ou diviser par un nombre décimal. |
|
|
Pourcentages par exemple : 10 %, 42 % |
Lire et écrire des pourcentages. Établir le rapport de pourcentage entre 2 nombres. Calculer le pourcentage d’un nombre. |
|
|
Équivalences par exemple : 1/2 = 0,5 = 50 % |
Convertir entre fractions, nombres décimaux et pourcentages. |
|
|
Autres nombres réels par exemple : v36, 92, 2,2 x 103, p |
Utiliser des puissances et des racines, des notations scientifiques, des chiffres significatifs. |
|
| Équations et formules | Résoudre des problèmes au moyen d’équations à une inconnue. Utiliser des formules en y insérant des quantités. Résoudre des équations quadratiques. |
|
| Taux, ratios et proportions |
Utiliser un taux comparant 2 quantités ayant des unités différentes. |
|
| Conversion de mesures |
Convertir des mesures impériales en mesures métriques (SI). |
|
| Superficies, périmètres et volumes | Calculer des superficies, des périmètres et des volumes. |
|
| Géométrie | Appliquer des concepts géométriques, par exemple le parallélisme, la perpendicularité et les tangentes. |
|
| Trigonométrie | Utiliser la trigonométrie pour déterminer la longueur d’un côté inconnu ou l’angle d’un triangle. |
|
| Calculs sommaires | Calculer des moyennes et des taux autres que des pourcentages, des proportions ou des rapports. |
Calculer des moyennes pour :
|
| Statistiques et probabilités | Utiliser des statistiques et des probabilités pour tirer des conclusions. |
|
Section 1 : Mesures et calculs
C’est pour mesurer que les chiffres sont utilisés le plus souvent dans les métiers. Les mesures et les calculs sont utilisés pour mesurer et décrire le monde physique, par exemple pour mesurer et calculer des superficies et des volumes. Voici 3 exemples typiques de mesure et de calcul au travail.
- Les électriciens et électriciennes en construction prennent des mesures et effectuent des calculs pour s’assurer que les installations électriques satisfont aux exigences du code de l’électricité.
- Les charpentiers et charpentières prennent des mesures précises à l’aide de matériel de mesure.
- Les plombiers et plombières effectuent des calculs trigonométriques pour dessiner, fabriquer et installer des tuyaux qui doivent contourner un obstacle.
Instruments de mesure
Les compagnons et les compagnes qui construisent des choses à leur travail utilisent à tous les jours des rubans à mesurer, du matériel de mesure au laser, des micromètres, des échelles et d’autres instruments pour mesurer des grandeurs. Ils travaillent avec des mesures impériales et avec des mesures métriques.
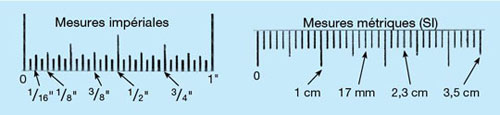
1. Veuillez inscrire la longueur exacte à côté de chaque flèche sur le ruban à mesurer. Rappelez-vous d’inscrire les bonnes unités (pouces ou centimètres). Deux exemples vous sont donnés.
-
Réponse :

Principes mathématiques : Nombre entiers, fractions, nombres décimaux (impérial, métrique)
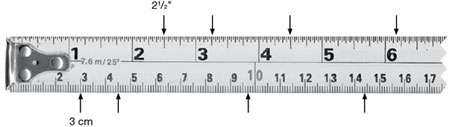
2. Veuillez marquer ce ruban à mesurer aux points suivants (a–f) avec une flèche en indiquant la lettre de la question. Deux exemples vous sont donnés.
x. 37 1/2" y. 1,01 m
a.39 1/8 po.
b.3 pi. 4 3/4 po.
c. 3,5 pi.
d. 93 cm
e. 0,992 m
f. 107,5 cm
-
Réponse :

Principes mathématiques : Nombre entiers, fractions, nombres décimaux (impérial, métrique)
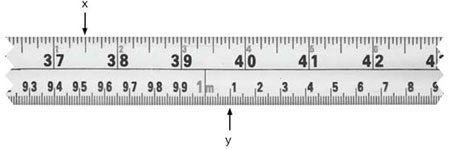
3. Les charpentiers et charpentières prennent des lectures des élévations, des directions et des longueurs des limites de propriété au moyen d’une mire de nivellement. Les chiffres en rouge sur la mire représentent le nombre de pieds et les chiffres en noir, les dixièmes de pied.
Inscrivez les lectures ci-dessous. Les 2 premières ont été faites pour vous.
Note : Les chiffres en rouge sont plus gros que les chiffres en noir lorsqu’ils marquent un nombre entier de pieds (par exemple, 3,0 pieds), mais plus petits lorsqu’ils servent de « rappel » entre des dixièmes de pied.

-
Réponse :
Question 3a :
- 7,32 pieds
- Prinicpes mathématiques : Nombre entiers, nombres décimaux
Question 3b :
- 5,12 pieds
- Principes mathématiques : Nombre entiers, nombres décimaux
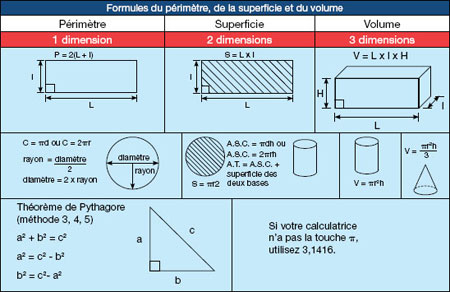
Formules
Les formules présentées dans l’encadré qui suit vous aideront à résoudre les problèmes qui sont proposés dans la présente section.
Que ce soit à l’école ou au travail, il serait utile que vous développiez votre propre méthode de résolution de problèmes mathématiques faisant intervenir des mesures. Les étapes décrites ci-dessous peuvent vous aider à y parvenir.
Étapes :
- Dessinez un diagramme en indiquant les mesures connues.
- Déterminez quels renseignements il vous faut.
- Pensez aux unités avec lesquelles vous travaillez (par exemple, mètres carrés, charges, pieds).
- Décidez quelle(s) formule(s) vous devez utiliser.
- Calculez la réponse.
Note : Utilisez votre calculatrice pour répondre aux questions contenues dans le cahier d’exercices.
L’utilisation d’une calculatrice au travail vous permet d’économiser du temps. Familiarisez vous avec votre calculatrice pour pouvoir exploiter toutes ses caractéristiques.
-
Un charpentier/une charpentière construit une clôture temporaire autour d’un chantier de construction. Combien de mètres de clôture faut-il pour un chantier qui mesure 47,8 m sur 30,3 m? Arrondissez votre réponse au mètre près.
Utilisez les étapes de la résolution de problèmes :
- Dessiner
- Décider
- Calculer
-
Réponse :
2 (47,8 m + 30,3 m) = 156,2 = 157 m
Principes mathématiques : Périmètre (métrique)
- De combien de montants un charpentier/une charpentière aura-t-il/elle besoin pour faire tenir les murs extérieurs du bâtiment ci-dessous? Utilisez la formule ci-dessous pour estimer le nombre de montants.
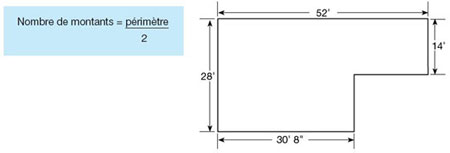
-
Réponse :
52' + 14' + (52' – 30' 8") + (28' – 14 ‘) +
30' 8" + 28' = 160'
160 ÷ 2 = 80 montants
Principes mathématiques : Périmètre (impérial)
-
-
De combien de contenants de 3,7 L de produit de collage un poseur/une poseuse de revêtements souples a-t-il/elle besoin pour installer un revêtement de sol en feuilles de vinyle dans une pièce qui mesure 9,2 m sur 7,8 m?
Seuls des contenants entiers peuvent être commandés.
Truelle type recommandée
(profondeur, largeur, espacement)Couverture approximative Truelle Feuilles de vinyle à endos de feutre fibreux :
1/32" × 1/16" × 1/32"
(0,8 mm × 1,6 mm × 0,8 mm)185–245 pi. ca./gallon américain
(4,5–6,0 m2/L)
-
Réponse :
9,2 m × 7,8 m = 71,76 m2
71,76 m2 ÷ 4,5 m2/L = 15,95 L
15,95 L ÷ 3,7 L = 4,31 = 5 contenants
Principes mathématiques : Superficie (métrique)
-
-
Un briqueteur-maçon/une briqueteuse-maçonne doit couvrir un terrain de jeux de tuiles en caoutchouc. La tuile de 2 pi2 se vend 13,29 $. Calculez combien il en coûtera pour couvrir le terrain de jeux.
Note : Seules des tuiles entières peuvent être commandées, de sorte que vous devrez arrondir votre réponse lorsque vous calculerez combien de tuiles sont nécessaires.

-
Réponse :
3,1416 (8,2 pi. × 8,2 pi. ) = 211,24 pi. 2
(211,24 pi. 2 ÷ 2 pi. 2/tile) = 105,62 = 106 tiles
106 tuiles × $13,29/tuiles = $1 408,74
Principes mathématiques : Superficie (impérial)
-
-
Un horticulteur-paysagiste/une horticultrice-paysagiste doit commander suffisamment de sable pour créer une bordure de 152 mm de profond autour d’une surface carrée, comme on peut le voir plus bas Combien de mètres cubes de sable sont nécessaires?

-
Réponse :
(14 m)2 – (9,25 m)2 = 110,44 m2
110,44 m2 × 0,152 m = 16,79 m3
Principes mathématiques : Volume (métrique)
-
-
Un manœuvre en construction veut savoir quelle quantité de matière se trouve dans le tas en forme de cône indiqué plus bas. Calculez le volume approximatif du tas en verges cubes.
Utilisez la formule suivante pour calculer le rayon d’un tas de matière :
r = ¾ × hauteur
27 pi.3 = 1 vg.3
-
Réponse :
r = ¾ × 16 pi. = 12 pi.
(3,1416 × (12 pi. )2 × 16 pi. ) ÷ 3 = 2 412,75 pi.3
2 412,75 pi.3 ÷ 27 pi. 3/vg.3 = 89,36 vg.3
Principes mathématiques : Volume (impérial)
-
-
Les calorifugeurs et calorifugeuses (chaleur et froid) couvrent des tuyaux pour garder les substances chaudes ou froides. Combien de mètres carrés de matériel sont nécessaires pour isoler un tuyau d’une longueur de 6 m et d’un diamètre de 2 m?
Imaginez que vous déroulez le cylindre, de sorte que la circonférence devient la mesure de la largeur.
Utilisez cette formule : pdh

-
Réponse :
3,1416 × 2 m × 6 m = 37,6992 = 37,7 m2
Principes mathématiques : Superficie (métrique)
-
- Les électriciens et électriciennes calculent la résistance totale de circuits électriques parallèles. Utilisez la formule ci-dessous pour calculer la résistance totale du circuit illustré plus bas.
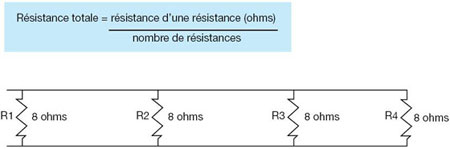
-
Réponse :
8 ohms ÷ 4 résistances = 2 ohms
Principes mathématiques : Équations et formules
-
- Les plombiers et plombières doivent ajouter des bouts de tuyaux pour réaliser des travaux particuliers. Quelle est la longueur centre à centre (c–c) du tuyau illustré plus bas?

-
Réponse :
222 + 182 = 808
v808 = 28,43 cm
Principes mathématiques : Trigonométrie
-
- Les charpentiers et charpentières effectuent des calculs qui les aident à dessiner et à construire un escalier en bois. Calculez la longueur du limon (c) pour l’escalier illustré plus bas.

-
Réponse :
1 0002 + 1 2552 = 2 575 025
v2 575 025 = 1 605 mm
Principes mathématiques : Trigonométrie
-
- Les mécaniciens et mécaniciennes de réfrigération et d'air climatisé et les ferblantiers et ferblantières construisent et installent des coudes de transition pour raccorder des conduits de dimensions différentes. Calculez la longueur du côté diagonal du coude de transition ci-dessous.
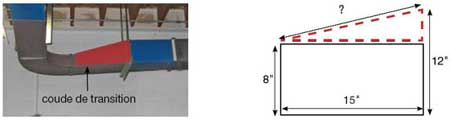
-
Réponse :
152 + (12– 8)2 = 241
v241 = 15,52 pouces
Principes mathématiques : Trigonométrie
-
- Les plombiers et plombières calculent la pression d’eau en livres par pouce carré (psi). Quelle est la pression d’eau dans un tuyau vertical de 28 pieds plein d’eau?
Utilisez cette formule :
Pression d’eau (psi) = h × 0,433
-
Réponse :
28 × 0,433 = 12,12 psi
Principes mathématiques : Équations et formules
-
- Les ferblantiers et ferblantières installent des conduits dans des bâtiments.
L’équation ci-dessous montre la relation qui existe entre :
- le volume de débit d’air en pieds cube par minute (V),
- la vitesse de l’air en pieds par minute (v) et
- la superficie d’une coupe en travers d’un conduit en pieds carrés (A).
V = A × v
a. Calculez la superficie en pieds carrés d’une coupe en travers d’un conduit de 8 po. × 24 po..
1 pi.2 = 144 po.2
b. Calculez le volume de débit d’air si la vitesse de l’air dans le même conduit est de 1 200 pieds à la minute.
-
Réponse :
Question 13a.
- 8 po. × 24 po. = 192 po. 2
- 192 po. 2 ÷ 144 po. 2/pi. 2 = 1,33 pi. 2
- Principes mathématiques : Superficie (impérial)
Question 13b.
- 1,33 pi. 2 ×1 200 pi. /min = 1 596 pi. 3/min
- Principes mathématiques : Équations et formules
Dessins
Les compagnons et les compagnes qui travaillent sur un chantier de construction suivent les spécifications d’un ensemble de dessins ou d’imprimés qui montrent différents aspects du projet de construction terminé. Les compagnons et les compagnes de tous les domaines examinent les dessins pour obtenir l’information détaillée dont ils ont besoin.
Les compagnons et les compagnes convertissent souvent des pouces en fractions ou en décimales d’un pied.
3 po. = ¼ pi. ou 0,25 pi.
6 po. = ½ pi. ou 0,5 pi.
9 po. = ¾ pi. ou 0,75 pi.
12 po. = 1,0 pi.
Additionner ou soustraire des pieds et des pouces :
Étape 1 : Enligner les mesures de manière que les mêmes unités figurent les unes sous les autres.
Étape 2 : Additionner ou soustraire les pouces. Additionner ou soustraire les pieds.
Étape 3 : Changer les pouces en pied (diviser par 12).
Étape 4 : Additionner le chiffre que vous avez obtenu à l’étape 3 au chiffre que vous avez obtenuà l’étape 2.
Exemple :
Étape 1
7 pi. 11 po.
+ 2 pi. 9 po.
___________
Étape 2
7 pi. 11 po.
+ 2 pi. 9 po.
___________
9 pi. 20 po.
Étape 3
20 po. = 1 pi. 8 po.
Étape 4
9 pi.
+ 1 pi. 8 po.
___________
10 pi. 8 po.
Examinez le dessin se rapportant à une résidence qui figure à la page suivante.
- La penderie mesure 1¼ po. × 1½ po. sur le dessin Quelles sont ses dimensions réelles?
-
Réponse :
5/4 × 1 pi. = 5 pi.
3/2 × 1 pi. = 6 pi.
Dimensions = 5 pi. × 6 pi.
Principes mathématiques : Taux, ratios et proportions
-
- Combien de portes coulissantes (portes à glissière) faut-il?

-
Réponse :
3
Principes mathématiques : Nombres entiers
-
- Quelle est la longueur extérieure entre A et B ?
-
Réponse :
2' 2" + 8' + 2' 2" = 12' 4"
Principes mathématiques : Conversions de mesures
-
- Le tapis se vend 28,50 $ la verge carrée. Combien coûte le tapis de la chambre principale et de la penderie?
1 vg. 2 = 9 pi. 2
-
Réponse :
S = 12 pi. ×14 pi. = 168 pi. 2
168 pi. 2 + 30 pi. 2 = 198 pi. 2
198 pi. 2 ÷ 9 pi. 2/vg. 2 = 22 vg. 2
$28,50/vg. 2 × 22 vg. 2 = $627,00
Principes mathématiques : Superficie, conversions de mesures
-
- Estimez le nombre de panneaux de gypse nécessaires pour les murs de la salle de bains attenante.
Panneaux de gypse : 4 pi. × 8 pi.
Hauteur de la pièce : 8 pi.
Largeur des portes coulissantes : 3 pi.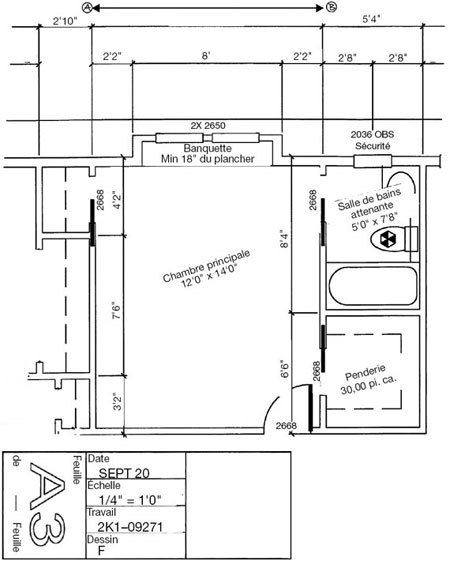
-
Réponse :
Méthode 1 :
- Hauteur des panneaux de gypse = hauteur de la pièce
- 5 pi. + 7,67 pi. + 5 pi. + 7,67 pi. = 25,34 pi.
- 25,34 pi. – 3 pi. = 22,34 pi.
- 22,34 pi. ÷ 4 pi. /feuille = 5,585 = 6 panneaux
Méthode 2 :
- 5 pi. + 7,67 pi. + 5 pi. + 7,67 pi. = 25,34 pi.
- 25,34 pi. – 3 pi. = 22,34 pi.
- 22,34 pi. × 8 pi. = 178,72 pi. 2
- 4 pi. × 8 pi. = 32 pi. 2
- 178,72 pi. 2 ÷ 32 pi. 2 = 5,585 = 6 panneaux
Principes mathématiques : Nombres décimaux
-
Calcul des poids
Les opérateurs et opératrices de grue automotrice ont à calculer des poids. Le fait de calculer la charge de sécurité protège le matériel, les matériaux qu’il transporte, les travailleurs sur le chantier et le grand public.
Exercice pratique
Calculez le poids d’une plaque en aluminium de 4' × 18" d’une épaisseur de 3/8".
Une plaque d’aluminium d’une épaisseur de 1/8" pèse environ 1,75 livre par pied carré.

Étapes :
-
Dessiner un diagramme et le marquer des mesures voulues.
-
Calculer la superficie.
Superficie = Longueur × largeur
Superficie = 4 pi. × 1,5 pi.
Superficie = 6 pi.2 -
Calculer le poids.
a) Poids d’une plaque en aluminium de
1 pi.2 et de 3/8 po. d’épaisseur : --> 3/8 po. ÷ 1/8 po. = 3 --> 1,75 lb./pi.2 × 3 = 5,25 lb./pi.2b)
Superficie de la plaque
× Poids au pied carré
_____________________
= Poids en livre6 pi.2
× 5,25 lb./pi.2
_______________
= 31,5 lb.La plaque en
aluminium pèse environ
31,5 livres.
- Les chaudronniers et chaudronnières et les monteurs et monteuses de charpentes en acier doivent calculer le poids des matières qu’ils utilisent pour fabriquer leurs produits. Calculez le poids approximatif d’une plaque d’acier de 2 pi. × 18 pi. de ¾ po. d’épaisseur.
Une plaque d’acier de 1" pèse environ 40 lb./pi.2
-
Réponse :
2 pi. × 18 pi. = 36 pi.2
¾ × 40 lb. /pi. 2 = 30 lb. /pi.2
36 pi.2 × 30 lb. /pi. 2 = 1 080 lb.
Principes mathématiques : Équations et formules
-
-
Un opérateur et une opératrice de grue automotrice calcule le poids d’un panneau de béton pour s’assurer que la grue peut le lever en toute sécurité. Calculez le poids approximatif du panneau illustré plus bas.
Du béton armé pèse environ 150 lb./pi.3.
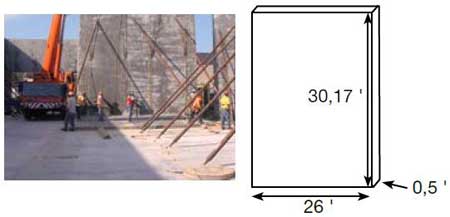
-
Réponse :
26' × 30.17' × 0.5' = 392,21 pi.3
392,21 pi.3 × 150 lb. /pi.3 = 58 831,5 lb.
Principes mathématiques : Équations et formules
-
Quantités
Les taux et les ratios sont utilisés pour comparer 2 quantités. Tous 2 peuvent être exprimés dans les formes suivantes : 1 sur 2, 1:2 ou ½.
Les taux comparent 2 quantités ayant des unités différentes. Par exemple, un taux peut servir à décrire le débit d’un liquide en litres par seconde.
Exemple: 1 cuillerée à table de farine pour une tasse de lait.
Les ratios comparent 2 quantités ayant les mêmes unités. Par exemple, un ratio peut servir à décrire le nombre de parties d’eau et le nombre de parties d’agents colorants qui doivent être combinées.
Exemple : 1 partie d’eau / 2 parties de ciment
Les proportions comparent 2 ratios ou 2 taux.
- Une canalisation d’égout accuse une pente de ¼" par pied. Calculez la distance totale de chute sur 30 pieds.
Utilisez cette formule :
Distance totale de chute = longueur × pente-
Réponse :
Distance totale de chute = 30 pi. × ¼ po. /pi. = 7,5 pi.
Principes mathématiques : Taux, ratios et proportions
-
- Les mécaniciens et mécaniciennes de véhicules automobiles doivent parfois convertir des kilomètres en milles pour des clients américains. Un changement d’huile doit être fait à 35 000 km. Quelle est la même distance en milles?
1 km = 0,6214 mi.
-
Réponse :
35 000 km × 0,6214 mi./km = 21 749 mi.
Principes mathématiques : Taux, ratios et proportions
-
- Un coiffeur/une coiffeuse prépare un traitement capillaire. Le client a les cheveux longs. Le coiffeur commence avec 1¼ godet de poudre décolorante.
Préparation : Mettre 1 godet comble de poudre décolorante dans un bol ou une bouteille non métallique. Ajouter 1 oz. (30 g) de renforçateur et 2 onces liquides (60 mL) de crème revitalisante. Bien mélanger jusqu’à consistance crémeuse.
- Calculez le nombre de grammes de renforçateur nécessaires.
- Calculez le nombre de millilitres de crème revitalisante nécessaires.
-
Réponse :
Question 3a :
- 5/4 × 30 g = 37,5 g
- Prinicipes mathématiques : Taux, ratios et proportions
Question 3b :
- 5/4 × 60 mL = 75 mL
- Prinicipes mathématiques : Taux, ratios et proportions
- Les cuisiniers et cuisinières changent souvent le rendement des recettes pour servir plus de clients ou moins de clients. La recette qui suit fait 30 crêpes. Adaptez la recette pour faire 75 crêpes.
Servez-vous des proportions pour calculer quelle quantité d’ingrédient est nécessaire pour faire la recette. Nous avons fait les calculs pour le premier ingrédient selon 2 méthodes différentes :
Méthode 1:
625 g = ? g
____ ____
30 75625 x 75 = 46 875 ÷ 30 = 1 562,5 g
____
30Méthode 2:
625 ÷ 30 = 20,883
75 x 20,833 = 1 562,5 g
Ingrédient Quantité pour 30 Quantité pour 75 Farine 625 g 1 562,5 g Sucre 60 g Poudre à pâte 30 g Œufs 4 Lait 1 L Beurre fondu 125 g -
Réponse :
quantité × 75 = quantité d’ingrédients
___________
30sucre 150 g, poudre à pâte 75 mL,
œufs 10, lait 2,5 L, beurre 312,5 g
Principes mathématiques : Taux, ratios et proportions
-
- Les étiquettes des produits donnent de l’information sur les quantités à mélanger. Utilisez l’étiquette pour répondre aux questions ci-dessous.
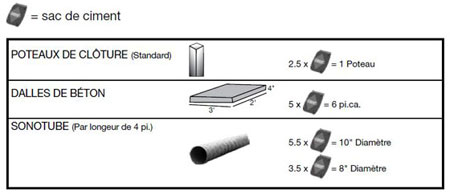
- Un charpentier/une charpentière construit une clôture qui a 9 poteaux. Combien de sacs de ciment faut-il pour fixer les poteaux?
- Calculez le nombre de sacs de ciment nécessaires pour une dalle qui mesure 5' × 2' 4" × 6".
- Des formes tubulaires sont utilisées pour former les colonnes de ciment. Le ciment est mélangé à raison de 2,5 litres d’eau par sac de mélange à ciment. Calculez la quantité d’eau requise pour une colonne de 15 pieds ayant un diamètre de 8 pouces.
-
Réponse :
Question 5a :
- 9 poteaux × 2,5 sacs/poteau = 22,5 = 23 sacs
- Principes mathématiques : Taux, ratios et proportions
Question 5b :
- 5 sacs = 3 pi. × 2 pi. × 0,33 pi. = 1,98 pi.3
- 5 pi. × 2,33 pi. × 0,5 pi. = 5,825 pi.3
- 5,825 pi.3 ÷ 1,98 pi.3 = 2,94
- 2,94 × 5 sacs = 14,7 = 15 sacs
- Principes mathématiques : Taux, ratios et proportions
Question 5c :
- 15 pi. ÷ 4 pi. = 3,75
- 3,75 x 3,5 = 13,125 = 14 sacs
- 14 sacs x 2,5 L/sac = 35 litres d’eau
- Principes mathématiques : Taux, ratios et proportions
Section 2 : Calculs monétaires
Les calculs monétaires sont utilisés pour donner ou recevoir de l’argent au travail, par exemple pour manipuler de l’argent comptant, préparer des factures ou faire des paiements. Voici 3 exemples types de calculs monétaires faits au travail.
- Les cuisiniers et cuisinières utilisent la petite caisse pour acheter de petites quantités de fournitures dont ils ont besoin immédiatement.
- Les coiffeurs et coiffeuses préparent des factures et perçoivent de l'argent comptant et des paiements par carte de débit ou de crédit pour leurs services. Ils facturent des services selon les taux établis et ajoutent les taxes applicables telles que la TPS.
- Les mécaniciens et mécaniciennes de véhicules automobiles calculent le coût total des travaux de réparation, y compris les pièces, la main-d’œuvre, les suppléments et les taxes, et entrent les chiffres sur des formules d’estimation ou sur des bons de travail lorsque tout est terminé.
Augmentations et diminutions
Calculer des augmentations
Dans certains magasins, les produits sont achetés au prix de gros et vendus au prix de gros majoré de la marge brute. Voici une façon de calculer la marge brute ou la taxe de vente.
| Méthode | Exemples |
|---|---|
|
Marge brute
|
Un article acheté à un prix de gros de 14,35 $ est vendu à un prix majoré de 22 %. Calculer le prix de vente. 100 % + 22 % = 122 % 122/100 = 1,22 1,22 × 14,35 $ = 17,507 $ = 17,51 $ |
|
Taxe de vente
|
Calculer le coût après taxe de 2 heures de main d’œuvre au taux horaire de 45 $. 2 heures × 45,00 $ = 90,00 $ coût de main d’œuvre. 100 % + 7 % = 107 % 107/100 = 1,07 1,07 × 90,00 $ = 96,3 $ = 96,30 $ |
Calculer des rabais
Les produits sont parfois vendus à rabais lorsqu’ils sont discontinués ou que le fournisseur a une promotion. Voici une façon de calculer un rabais.
| Méthode | Exemple |
|---|---|
|
Un article vendu régulièrement 10,89 $ est réduit de 15 %. Calculer le prix de vente. 100 % – 15 % = 85 % 85/100 = 0.85 0,85 × 10,89 $ = 9,257 $ = 9,26 $ |
- Dans un salon de coiffure, les prix du revient des produits sont majorés de la marge brute avant la revente. Calculez les prix de vente.
Prix de gros Marge brute Prix de vente a. 97,25 $ 10 % b. 249,99 $ 15 % c. 6,50 $ 8 % -
Réponse :
Question 1a :
- (1,00 + 10/100) × 97,25 $ = 106,98 $
- Principes mathématiques : Pourcentages
Question 1b :
- 1,15 × 249,99 $ = 287,49 $
- Principes mathématiques : Pourcentage
Question 1c :
- 1,08 × 6,50 $ = 7,02 $
- Principes mathématiques : Pourcentage
-
- Calculez le coût après taxe des articles ci-dessous.
Coût Taxe Total a. 73,50 $ 12 % b. 1 847,00 $ 13 % c. 86,75 $ 8 % -
Réponse :
Question 2a :
- 1,12 × 73,50 $ = 82,32 $
- Principes mathématiques : Pourcentage
Question 2b :
- 1,13 × 1,847 $ = 2 087,11 $
- Principes mathématiques : Pourcentage
Question 2c :
- 1,08 × 86,75 $ = 93,69 $
- Principes mathématiques : Pourcentage
-
-
Dans un salon de coiffure, des produits sont vendus à des prix réduits à des fins de promotion. Calculez les prix de vente.
Prix Rabais Prix de vente a. 85,40 10 % b. 1 348,00 33 % c. 459,75 40 % -
Réponse :
Question 3a :
- (1,00 – 10/100) × 85,40 $ = 76,86 $
- Principes mathématiques : Pourcentage
Question 3b :
- 0,67 × 1 348 $ = 903,16 $
- Principes mathématiques : Pourcentage
Question 3c :
- 0,60 × 459,75 $ = 275,85 $
- Principes mathématiques : Pourcentage
-
Facturation des services
Les compagnons et les compagnes qui installent, entretiennent et réparent du matériel font souvent des factures pour les services qu’ils rendent et sont payés en argent comptant, par chèque ou par carte de crédit à leur travail. Le calcul de la taxe est une tâche typique dans ces cas-là.
1. a) Compléter la facture qui figure à la page suivante pour les services décrits ci-dessous :
- Réparer le lave vaisselle
- Modèle no MDB7601AWW
- Nettoyer la pompe, essai concluant
- Main d’œuvre 1,2 heure @ 88,25 $ de l’heure (5 % TPS)
- Pièces 2,80 $ (5 % TPS + 6 % TVP)
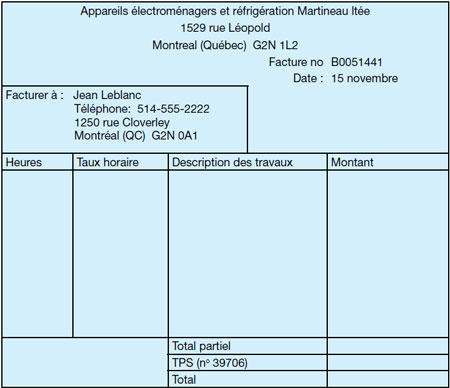
b) Le client paie la facture en argent comptant en utilisant les montants suivants :
1 × 100 $
1 × 20 $
1 cent
Combien de monnaie le technicien devrait-il remettre au client? Entrez les montants d’argent qui pourraient être remis comme monnaie. (Plusieurs réponses sont correctes.)
| 50 $ | 20 $ | 10 $ | 5 $ | 2 $ | 1 $ | 25 ¢ | 10 ¢ | 5 ¢ | 1 ¢ |
|---|---|---|---|---|---|---|---|---|---|
-
Réponse :
Question 1a :
- 105,90 $ × 1,05 = 111,20 $ (main-d’œuvre)
- 2,80 $ × 1,11 = 3,11 $ (pièces)
- 111,20 $ + 3,11 $ = 114,31 $
- Principes mathématiques : Nombres décimaux
Question 1b :
Monnaie : 120,01 $ – 114,31 $ = 5,70 $
50 $ 20 $ 10 $ 5 $ 2 $ 1 $ 25 ¢ 10 ¢ 5 ¢ 1 ¢ 1 2 2 Principes mathématiques : Nombres décimaux
Section 3 : Calendriers des budgets et des opérations comptables
Des calendriers des budgets et des opérations comptables sont utilisés pour gérer le temps et l’argent, par exemple pour planifier l’utilisation de votre temps et de votre argent et consigner la façon dont vous utilisez votre temps et votre argent, pour choisir les produits ou les services qui offrent le meilleur rapport qualité prix ou pour utiliser votre temps et votre argent judicieusement. Voici 3 exemples typiques d’établissement de calendriers des budgets et des opérations comptables en milieu de travail.
- Les mécaniciens industriels et mécaniciennes industrielles (de chantier) planifient des travaux pour des projets de construction, de réparation et d'entretien. Ils élaborent aussi des calendriers pour l'entretien du matériel des usines de transformation.
- Les machinistes adaptent les horaires de travail quotidiens pour faire de la place aux travaux urgents ou aux travaux qui prennent plus de temps que prévu. Par exemple, ils peuvent être appelés à modifier les procédés d'usinage ou l'ordre d'exécution des travaux. Ils déterminent si des collègues sont touchés par les changements au déroulement du travail et essaient de réduire le plus possible les perturbations.
- Les cuisiniers et cuisinières établissent des budgets hebdomadaires qui comprennent les coûts des aliments frais, des produits en magasin, du nombre d’employés qu’il faut, etc. En outre, ils établissent des budgets distincts pour chacun des services de traiteur pour la semaine. Cela variera en fonction des produits au menu, du nombre de services et du nombre de personnes que l'on sert.
Comparaison de valeurs
Utilisez un tableau pour comparer des articles.
| Points de comparaison | Article 1 | Article 2 | Article 3 |
|---|---|---|---|
| Coût 1 | |||
| Coût 2 | |||
| Coût 3 |
Pour résoudre les problèmes proposés dans cette section, vous devez repérer et comprendre l’information contenue dans les documents.
Les produits de revêtement peuvent être appliqués à la truelle ou au rouleau.
-
Un finisseur/une finisseuse de béton estime le coût à engager pour refaire la surface du trottoir qu’on peut voir sur la photo ci-contre selon 2 méthodes d’application du ciment différentes. La méthode de la truelle a des effets plus durables, mais coûte plus cher. Étant donné l’information ci-dessous, estimez la différence de coût.
- Le finisseur/la finisseuse de béton demande 37,50 $ de l’heure.
- Il faut 1 heure et 30 minutes environ pour appliquer chaque revêtement.

| Composant | 9,29 m2
(100 pi. ca. ) |
18,58 m2
(200 pi. ca. ) |
27,87 m2
(300 pi. ca. ) |
37,16 m2
(400 pi. ca. ) |
|---|---|---|---|---|
| Aucun apprêt requis | ||||
| Étape 1: Revêtement à pierre appliqué au rouleau 89,00 $/9,2 L |
1 × 9,2 L | 2 × 9,2 L | 3 × 9,2 L | 4× 9,2 L |
| Étape 2 : Revêtement extérieur de protection 26,78 $/946 mL |
1 × 946 mL | 2 × 946 mL | 1 × 3,78 L | 1 × 3,78 L |
| Composant | 9,29 m2
(100 pi. ca ) |
18,58 m2
(200 pi. ca ) |
27,87 m2
(300 pi. ca ) |
37,16 m2
(400 pi. ca ) |
|---|---|---|---|---|
| Étape 1: Apprêt 48,20 $/3,78 L |
1 × 3,78 L | 1 × 3,78 L + 1 × 946 mL |
2 × 3,78 L | 3 × 3,78 L |
| Étape 2 : Revêtement à pierre appliqué à la truelle 115,07 $/15,1 L 53,25 $/3,78 L |
1 × 15,1 L + 2 × 3,78 L |
3 × 15,1 L | 4 × 15,1 L + 2 × 3 78 L |
6 × 15,1 L |
| Étape 3 : Revêtement extérieur de protection 26,78 $/946 mL |
1 × 946 mL | 2 × 946 mL | 1 × 3,78 L | 1 × 3,78 L |
-
Réponse :
Superficie du trottoir = 32 pi. × 3 pi. = 96 pi. 2
Rouleau : (1,5 h × 2) × 37,50 $/h = 112,50 $
89,00 $ + 26,78 $ = 115,78 $
112,50 $ + 115,78 $ = 228,28 $
Truelle : (1,5 h × 3) × 37,50 $ = 168,75 $
48,02 $ + 115,07 $ + (2 × 53,25 $) +
26,78 $ = 296,55 $
168,75 $ + 296,55 $ = 465,30 $
465,30 $ – 228,28 $ = 237,02 $
La méthode de la truelle coûte environ 240,00 $ de plus.
Principes mathématiques : Nombres décimaux
Comptabilité des coûts de revient
De nombreux compagnons et les compagnes fournissent des estimations aux clients. Ils doivent alors dire au client quel montant celui-ci devrait s’attendre à payer à peu près pour un article donné.
Dans l’exemple ci-dessous, compagnons et les compagnes estime qu’un évier coûtera 100 $. Si l’évier n’est pas acheté ou coûte moins de 100 $, l’économie figurera entre parenthèses, ce qui signifie que le coût réel est inférieur au coût budgété.
| Article | Coût estimé ($) | Coût réel ($) | Différence +/- ($) |
|---|---|---|---|
| Évier | 100,00 | 75,99 | (24,01) |
Si l’évier coûte plus que 100 $, le coût supplémentaire est indiqué sans parenthèses, ce qui signifie que le coût réel dépasse le coût budgété.
| Article | Coût estimé ($) | Coût réel ($) | Différence +/- ($) |
|---|---|---|---|
| Évier | 100,00 | 123,67 | 23,67 |
-
Les compagnons et les compagnes comparent les estimations avec les coûts réels. Après que le client a choisi l’article qu’il veut acheter, la personne de métier peut lui dire de combien le coût réel sera inférieur ou supérieur au coût estimé.
Utilisez la facture de rénovations qui figure à la page suivante pour répondre aux questions ci-dessous.
- Comparez le coût estimé du revêtement de plancher au coût réel Inscrire la différence sur la facture.
- Un entrepreneur soumissionne des travaux de rénovation d’appartements et doit soumettre une estimation pour l’installation d’un miroir de salle de bains, d’un carrelage mural et d’une toilette identiques dans 5 unités. Utilisez les coûts réels inscrits sur la facture pour calculer l’estimation que l’entrepreneur devrait soumettre. Ajoutez 10 % pour tenir compte de la hausse des coûts.
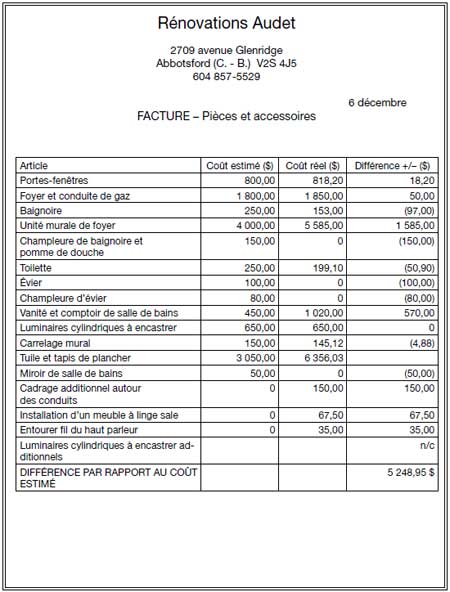
-
Réponse :
Question 1a :
- 3 050 $ – 6 356,03 $ = – 3 306,03 $
- Inscription sur la facture : (3 306,03 $)
- Principes mathématiques : Nombres entiers relatifs
Question 1b.
- (153,00 $ + 145,12 $ + 199,10 $) × 5 = 2 486,10 $
- 1,10 × 2 486,10 $ = 2 734,71 $
- Principes mathématiques : Nombres entiers relatifs, pourcentages
Section 4 : Analyse de données
L’analyse de données est utilisée pour résoudre des problèmes en analysant et en comparant des données. De plus en plus, il faut avoir ces compétences parce que les programmes informatiques facilitent l’accès aux données. Suivent 3 exemples typiques d’analyse de données au travail.
- Les mécaniciens et mécaniciennes de véhicules automobiles analysent les résultats des tests des systèmes électriques pour diagnostiquer les défectuosités, par exemple un véhicule qui ne démarre pas.
- Les machinistes analysent des données de contrôle de la qualité afin de relever des tendances quant au rendement de l'outillage. Par exemple, les machinistes peuvent devoir comparer les dimensions d'une pièce finie à intervalles réguliers au cours d'un cycle d'usinage afin de déterminer le moment où il faudra remplacer l'outillage ou régler l'équipement.
- Les électriciens et électriciennes en construction utilisent les résultats des mesures du courant (par exemple le courant consommé, les tensions à divers points, le couple et la température) à plusieurs points dans le circuit pour analyser le fonctionnement du circuit, diagnostiquer des anomalies électriques et accroître le rendement électrique.
Calcul de tolérances
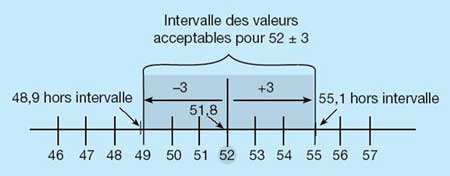
- Les ferblantiers et ferblantières, les machinistes, les mécaniciens et mécaniciennes de réfrigération et d'air climatisé et d’autres compagnons et compagnes doivent respecter des tolérances très serrées. Déterminez si les mesures présentées dans le tableau qui suit respectent les spécifications. Si les mesures respectent les spécifications, cochez à l'aide du symbole v, si non, inscrivez un x.
± signifie plus ou moinsSpécification Mesure v/X a. 22,5° ± 2° 20,1° b. 0,850 m ± 0,020 m 0,827 m c. 0,750 L ± 0,015 L 0,761 L -
Réponse :
Question 1a :
- X non acceptable
- 22,5° – 2° = 20,5°
- 20,1° n’est pas entre 20,5° et 22,5° = non acceptable
- Principes mathématiques : Nombres entiers relatifs
Question 1b.
- X non acceptable
- 0,850° – 0,020° = 0,830°
- 0,827° n’est pas entre 0,830° et 0,850° =
- non acceptable
- Principes mathématiques : Nombres entiers relatifs
Question 1c.
- ✓acceptable
- 0,750 L + 0,015 L = 0,765 L
- 0,761 L est entre 0,750 L et 0,765 L = acceptable
- Principes mathématiques : Nombres entiers relatifs
-
-
Un monteure/une monteuse de charpentes en acier prévoit utiliser une élingue câble d’acier de ¾ de pouce type bague pour lever une poutre qui pèse 4,6 tonnes. Recommandez une solution qui assurerait un levage plus sécuritaire. (Plusieurs réponses sont bonnes.)
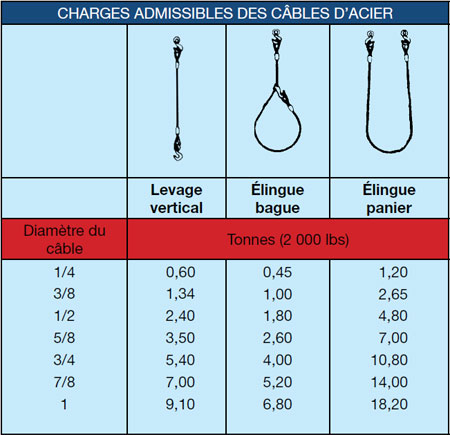
Note: Cette table de capacité a été conçue expressément pour le présent cahier d’exercices. Au travail, vous devriez utiliser la table du fabricant.
-
Réponse :
- utiliser un câble de 3/4" et un levage vertical (5,4 tonnes maximum)
- utiliser un câble de 7/8" et une élingue bague (5,2 tonnes maximum)
- Principes mathématiques : Nombres entiers relatifs
-
Utilisation des nombres dans des suites numériques
-
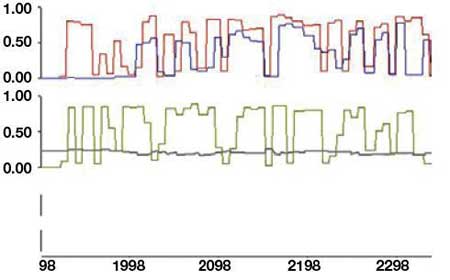
Les mécaniciens et mécaniciennes de véhicules automobiles utilisent du matériel de diagnostic pour analyser les problèmes dans les systèmes d’échappement. Lorsque le système fonctionne bien, l’axe des Y (l’axe vertical) sur le graphique devrait montrer des signaux qui oscillent constamment entre moins de 0,2 volt et plus de 0,8 volt.
Le graphique ci-dessous montre 2 séries de données numériques. La série du haut montre la lecture du moteur du côté du conducteur et la série du bas, la lecture du moteur du côté du passager.
Comment les courbes des 2 séries diffèrent-elles l'une de l'autre?
-
Réponse :
Dans la série du haut, les deux courbes fluctuent entre 0,2 volt et 0,8 volt. Dans la série du bas, seule une courbe affiche cette structure. L’autre courbe demeure presque plate, à environ 0,2 volt.
-