Guidance on the use of quantitative microbial risk assessment in drinking water

Download the entire report
(PDF format, 962 KB, 49 pages)
Organization: Health Canada
Type: Guidance
Date published: 2019-07-12
Health Canada
July, 2019
Table of Contents
- Acknowledgements
- Executive summary
- International considerations
- Part A. Guidance on the use of QMRA in drinking water
- A.1 Introduction and background
- A.2 Determining a risk assessment approach
- A.3 Sensitivity analyses: accounting for variability and uncertainty in risk assessment 3
- A.4 Assumptions and limitations associated with risk assessments
- A.5 Understanding risk estimates
- A.6 Application of QMRA in managing water safety
- Part B. HC QMRA Model Description
- Part C. References and acronyms
Acknowledgements
The development of the Health Canada QMRA model involved individuals from various organizations outside of Health Canada. In particular, the significant contributions of Ian Douglas and Joshua Elliott, City of Ottawa, are acknowledged.
Executive summary
Quantitative microbiological risk assessment (QMRA) is an approach that can be used by regulatory agencies and drinking water authorities to quantify the health risks from microorganisms for water sources. It follows a common approach that includes hazard identification, exposure assessment, dose-response assessment and risk characterization. QMRA can examine the entire drinking water system, from the source water to the consumer, to understand the potential impacts on public health. Health Canada has developed and uses a QMRA model to support the development of drinking water guidelines for enteric viruses and protozoa. The model can also be used as part of site-specific risk assessments at drinking water treatment facilities.
QMRA can be a very useful tool in support of water safety management decisions. A well-formulated and thoughtful QMRA can offer important information on prioritizing hazards, identifying alternative risk management priorities and options, selection of appropriate interventions, cost-benefit analysis of risk management actions and setting of health-based performance targets. It is important to remember that QMRA does not calculate actual disease outcomes, but provides a probability that disease may occur based on the water quality and treatment system information entered.
The intent of this document is to provide industry stakeholders, such as provincial and territorial regulatory authorities, decision-makers, water system owners, and consultants with guidance on the use of QMRA to assist in understanding microbiological risks in Canadian water systems.
International considerations
Drinking water guidelines, standards and/or guidance from other national and international organizations may vary due to the age of the assessments as well as differing policies and approaches.
QMRA is increasingly being applied by international agencies and governments at all levels as the foundation for informed decision-making surrounding the health risks from pathogens in drinking water. The World Health Organization (WHO), the European Commission, the Netherlands, Australia and the United States have all made important advances in QMRA validation and methodology. These agencies and governments have adopted approaches that use QMRA to inform the development of health targets and risk management for microbiological contaminants.
Part A. Guidance on the use of QMRA in drinking water
A.1 Introduction and background
The Guidelines for Canadian Drinking Water Quality encourage the adoption of a multi-barrier source-to-tap approach to produce clean, safe and reliable drinking water (Health Canada, 2013a). As part of this source-to-tap approach, quantitative microbial risk assessment (QMRA) can be used. QMRA can examine the entire drinking water system—from pathogens in the source water, through the treatment process, to the consumer—to understand the potential impact on public health. This is done following a common approach consisting of four components: hazard identification, exposure assessment, dose-response assessment and risk characterization. Following this approach, Health Canada developed a QMRA model that has been used to support the development of drinking water guideline values for enteric viruses and protozoa, and to encourage site-specific risk assessments at drinking water treatment facilities. The Health Canada QMRA (HC QMRA) model does not assess risks from the distribution system. A copy of the model can be obtained by request from hc.water-eau.sc@canada.ca.
The purpose of this document is two-fold: to provide an overview of the considerations, including the assumptions and limitations that are necessary for conducting site-specific risk assessments; and to describe the principles, equations, and literature values used by the HC QMRA model. The document is divided into two sections. Part A provides general guidance on the use of QMRA and is intended for individuals with an interest in, or responsibility for, drinking water quality and safety. Part B provides detailed information on the HC QMRA model along with some scenarios for its application. This information is intended for those interested in better understanding and potentially applying the QMRA tool developed by HC. By capturing general QMRA considerations (Part A) and detailed HC model development information (Part B) into one document, the intention is to provide a single document that can be used in Canada to improve understanding and implementation of QMRA as part of a source-to-tap approach. This document does not provide detailed instructions on how to carry-out site specific assessments. Examples of QMRA analyses of specific drinking water supplies can be found elsewhere (WHO, 2016; Bartrand et al., 2017a,b).
A.2 Determining a risk assessment approach
There is a spectrum of risk assessment approaches that can be used as part of a source-to-tap, or water safety plan approach to drinking water management. They range from qualitative to quantitative approaches. The WHO publication on risk assessment (WHO, 2016) provides a good overview of the strengths and limitations of the range of risk assessment approaches, along with general advice on when and how they should be applied. All risk assessment approaches, regardless of whether they are qualitative or quantitative, will provide utilities with a better understanding of their drinking water system and the potential risks associated with the supply. Implementing a risk assessment approach should not be a paper-only exercise. All risk assessment approaches require knowledgeable individuals to visually inspect the water supply system to identify both the conditions that could lead to the presence of microbial pathogens and the control measures in place to manage the risks.
The type of risk assessment needed for any given water system should be determined on a site-specific basis, as the type and level of microbial risks will vary between water systems. In general, the risk assessment approach used should balance the level of detail, complexity, and evidence, with the need for the use of assumptions and expert judgment, to implement an approach that is only as complicated as necessary to make decisions on risk management options (U.S. EPA, 2014; WHO, 2016).
The first step that should be undertaken when starting a risk assessment is to determine the scope of the assessment. This can be done by asking what question(s) need to be answered. Risk assessments can be initiated for a variety of reasons (U.S. EPA, 2014), including:
- assess the potential for human risk from exposure to a known pathogen;
- determine critical control points in the drinking water system;
- determine specific treatment processes to reduce the levels of various pathogens;
- predict the consequences of various management options for reducing risk;
- identify and prioritize research needs; and
- assist in epidemiological investigations.
Once the scope of the problem is defined, other key factors that should be considered when determining the appropriate type of risk assessment are the available human resources (e.g. personnel knowledge and skill levels, support from outside experts) and the type of supply system (e.g. small or remote system versus medium to large utility)(WHO, 2016).
The assessment can be qualitative, such as a sanitary inspection, or semi-quantitative, such as the use of risk matrices. For a qualitative assessment, this could be as simple as a checklist that accompanies the sanitary inspection whereby the number of 'yes' or 'no' answers determine a high, medium, or low risk component to the system. For example, depending on the question being asked, a small system using a protected groundwater source may not need to use anything more complicated than a qualitative assessment. However, if the qualitative assessment indicates high risk components to the system, then corrective actions or further investigation and assessment may be needed. As noted above, the risk assessment approach used should only be as complicated as necessary to answer the questions being asked. It is recommended, however, that all risk assessments provide some level of quantitation to help guide risk managers when prioritizing tasks (WHO, 2016).
Quantitative risk assessment approaches can range from screening assessments that use simple point estimates to full probabilistic risk assessments that include uncertainty analysis. QMRA models that use point estimates for the input variables, such as arithmetic mean values, are known as deterministic models. Probabilistic QMRA models use statistical distributions for the input variables, as opposed to single values. Defining these statistical distributions for each input variable requires more extensive data and knowledge than using a deterministic approach. Many risk assessment models combine both deterministic elements and probabilistic elements into the same model.
Quantitative risk assessments are also amenable to being applied as a tiered approach. For example, a screening level assessment could be used to provide guidance on whether the system is well-above, well-below, or just meeting allowable drinking water requirements. This information could then be used to help prioritize resources. In very data-limited situations, resources may be better used to implement system control measures based on the results of the screening assessment, as opposed to collecting the data necessary for a more in-depth, probabilistic assessment.
A.3 Sensitivity analyses: accounting for variability and uncertainty in risk assessment
Sensitivity analyses, which include variability and uncertainty evaluations, should be incorporated in risk assessment when possible. Variability is the natural variation in the components of a system and cannot be reduced. However, it can be better characterized by collecting additional data. Variability occurs in all components of a risk assessment, including pathogen concentrations, treatment performance, and dose-response characteristics. Uncertainty, on the other hand, is a reflection of the lack of understanding or inability to accurately measure some component that affects the outcome of the risk assessment. Uncertainty can arise from numerous sources, including a lack of information on the system under evaluation; limited local data that may not be representative of the range of values expected for that system; and from the statistical distributions selected to represent the data for the system (WHO, 2016). Uncertainty can be reduced through additional characterization of model input parameters.
Variability and uncertainty are routinely included as part of in-depth probabilistic assessments (i.e., stochastic models). They are captured using statistical distributions for the input parameters in the risk assessment model, based on the available data for the system. Adequately capturing the variability and uncertainty in the input parameters for use in probabilistic models is the most common obstacle to using a stochastic approach (U.S. EPA, 2014). Variability and uncertainty can also be included in screening level assessments using point estimates (i.e. deterministic models). In deterministic models, variability and uncertainty are usually captured by using scenarios (such as best-case and worst-case assumptions). This can help risk managers understand the probable range of risks. If a screening level assessment was conducted using only the upper limit of uncertainty for each parameter, the resulting risk estimate would be unmanageably conservative and not truly representative for the population. The use of scenarios can help determine next steps, including whether a system would benefit from a more complex stochastic modelling approach to refine their risk assessment, or whether resources would be better spent mitigating risk factors identified during the screening level assessment. WHO (2016) provides examples of how to incorporate variability and uncertainty into risk assessments. Both stochastic and deterministic models can also incorporate sensitivity analysis (U.S. EPA, 2014; WHO, 2016). In general, a sensitivity analysis is conducted by varying one input parameter (over its range of expected values), while keeping all other variables static at their baseline values, and recording the impact on the estimated health risk. As this process is repeated with all the variables of interest, it is possible to determine which variables have the greatest impact on the estimated health risk, i.e. how sensistive the model is to each input variable. This helps determine the risk drivers for a particular water system.
A.4 Assumptions and limitations associated with risk assessments
There are many assumptions and limitations surrounding risk assessment implementation for drinking water management. Assumptions are made by both the model developers in constructing risk assessment models, and by the analysts and managers regarding the data inputs to the risk assessment. For example, when developing a model, assumptions made by model developers include selecting the shape of the distribution to be applied to a given parameter (e.g., normal, log-normal, triangular), and determining the dose-response model that will be used for each pathogen. These assumptions are not usually modified during individual risk assessments. The assumptions included in the development of the HC QMRA model are described in Part B. For data inputs, assumptions may be needed in place of unknown or limited information, or to minimize the complexity of the assessment. In general, pathogen concentration estimates, treatment system efficacy, and exposure information are the model inputs that are subject to assumptions by risk analysts and risk managers. In order to properly interpret risk estimates, the limitations and assumptions associated with a risk assessment need to be well documented and understood.
A.4.1 Pathogen concentration estimates
Risk assessment models use pathogen concentrations to assess microbial risk and therefore, pathogen data is needed. In general, pathogen concentration estimates for a water source are limited by the amount of information available on both the uncertainty and the variability of the collected pathogen data. Pathogen data sets tend to be small, and may not fully capture the variability inherent to the system. Low pathogen densities and the episodic nature of pathogen loading add to the difficulty in capturing this variability (U.S. EPA, 2014). Also, many systems do not have any pathogen data and will need to rely on assumptions, published literature, expert judgement, or a combination of these. The methods available for detecting pathogens do not recover 100 percent of the pathogens in the samples, and recovery varies between samples, whcih needs to be taken into account when estimating concentrations. For some pathogens, method recovery data are not routinely determined and therefore a conservative estimate of recovery may need to be applied to ensure that the risk is not underestimated. There are numerous types of detection methods that can be used, which adds to the complexity of the data that is available in the literature as results from different methods may not be directly comparable. Many detection methods do not distinguish between pathogens that are capable of causing illness in humans and those that can not. This may include the detection of both viable and non-viable pathogens (e.g. using many molecular methods), or the detection of strains that are not known to cause illness in humans. Both of these situations can potentially lead to an overestimation of risk.
Due to the limitations associated with pathogen data, they should be used in conjunction with all the other information that is available for the system when conducting a risk assessment. Other information that could be used includes information from sanitary surveys, faecal indicator monitoring, microbial source tracking research, fate and transport modeling from faecal sources, or publications from the literature on the watershed or from other watersheds with similar faecal inputs (Ashbolt et al., 2010; U.S. EPA, 2014; WHO, 2016). All of these sources of information should be considered when making decisions regarding the pathogen concentration estimates for the system, including the associated variability and uncertainty. Further information can be found in section B.2.1.
A.4.2 Effectiveness of treatment barriers
Site-specific information on treatment barrier performance will provide the highest quality risk estimate. Utilities should make every effort to gather as much information as they can on their specific system using whatever data they have available, such as design parameters or performance assessments. Many systems will not have sufficient information to fully characterize their treatment performance and will, therefore, need to make some assumptions. There are numerous types and configurations of treatment barriers used to produce safe, reliable drinking water. Most of the commonly used treatment barriers have been extensively studied, and published literature is available on how effectively they reduce microbiological contaminants. Unfortunately, the ranges in removal for the same type of barrier can span up to 6 orders of magnitude depending on numerous factors such as water quality characteristics (e.g., temperature, organic content, pre-treatment), treatment plant design and operation (e.g., geometry, media, loading rates, hydrodynamics), and climatic factors (e.g., temperature, precipitation) (WHO, 2016). This variability in barrier performance can add significant uncertainty to a risk estimate if a drinking water system needs to rely solely on literature values. Further information on treatment barrier performance can be found in section B.3.
It is important to consider what level of detail is needed for the treatment system and then record all assumptions that are being made. Treatment barrier performance decisions should also consider the data that is routinely available, such as general source water quality data and operational data from the treatment plant.
A.4.3 Exposure analysis
When determining the exposure of individuals for the purposes of risk calculations, assumptions are usually made to simplify the risk assessment, as well as to apply the risk estimate to the entire population of the drinking water source. Generally, it is assumed that the route of exposure is limited to consumption of drinking water. This requires an assumption of the volume of water consumed by an individual on a daily basis. Depending on the risk assessment model, the volume of drinking water may be included as a point estimate, or as a distribution of values. Other assumptions that are commonly applied include that all individuals are equally susceptible to becoming infected. Some complex risk assessments may include variables for the immune status of the population as well as the potential for secondary spread of the pathogens to others in the community. However, this level of detail is not usually available. In addition, when the environmental exposure is expected to be low, as would be the case for treated drinking water, it has been demonstrated that similar risk estimates are obtained with or without the addition of susceptibility and secondary spread variables (Soller and Eisenberg, 2008). As such, these additional variables are not included in most drinking water risk modelling.
A.5 Understanding risk estimates
Risk estimates and health targets can be expressed on different time frames and using different metrics. Microbiological risks are usually estimated for daily exposures. The daily risks are then combined into an annual risk estimate. Tolerable health risk targets are usually expressed as annual risk targets, as opposed to daily risk targets. The advantage of annual targets is they allow for some variability in the water quality. For example, infrequent higher exposures can still occur as long they are balanced by days with much lower exposures so that the combined total for the year does not exceed the annual target. When using an annual target, it is important that it be set at a level that does not allow the variability in water quality to exceed what would be tolerable over a short term event. On the other hand, a daily target could be used to avoid the risks associated with a peak occurrence (Signor and Ashbolt, 2009).
The metrics that are generally used for expressing risk include the risk of infection or illness, or a health burden estimate such as disability adjusted life years (DALYs). The Guidelines for Canadian Drinking Water Quality use an annual target risk of 1 × 10−6 DALYs per person per year. This approach was adopted from the WHO (2004). The DALYs incorporates the severity and duration of the health effects associated with each pathogen. Pathogens with more severe health outcomes will have a greater DALYs weighting, which will result in a lower tolerable concentration to meet the risk target. Other jurisdictions, such as Netherlands, use a 1 × 10−4 annual risk of infection as the metric for comparison to a health target. The estimate of the DALYs health burden (DALYs per person per year) includes a step in which the annual risk of infection is calculated.
When interpreting risk estimates, there are numerous factors that need to be considered. First, the quality of the data that are included in the assessment needs to be understood. This includes the assumptions that were made, how they impact the risk estimates, and to what degree the variability and uncertainty has been captured during the assessment (including noting data gaps and sampling biases). Each input into a QMRA may be based, on assumptions and expert judgement, as long as the questions that need to be answered are amenable to this approach. The questions that need to be answered by the risk assessment require an in-depth probabilistic assessment, then the cost of collecting the data required for the analysis should be weighed against the cost of making resource decisions based on assumptions.
A.6 Application of QMRA in managing water safety
QMRA can be a very useful tool in support of water safety management decisions. QMRA does not calculate actual disease outcomes, but provides a probability that disease may occur through the water system (WHO, 2016). A well-formulated and thoughtful QMRA can offer important information on prioritizing hazards, identifying alternative risk management priorities and options, selecting appropriate interventions, cost-benefit analysis of risk management actions and setting of health-based performance targets. Inclusion of QMRA as part of a source-to-tap or water safety plan approach will require support for most utilities in the form of training, data showing and knowledge transfers. along with shared data and knowledge from individuals or organization with more experience. Understanding the underlying model assumptions, along with the objectives of the calculations and the limitations of the results is important to properly implement the use of QMRA (Petterson and Ashbolt, 2016). Overall, QMRA is an aid to assist in understanding your water systems and therefore, can provide valuable insight for risk management.
Part B. HC QMRA Model Description
B.1 HC QMRA model overview
The HC QMRA model was first developed more than 10 years ago to support the establishment of drinking water guidelines. Since its initial development, it has undergone numerous reviews and updates. In order to provide a tool that can be used by stakeholders to assess, on a site-specific basis, the potential impacts of changes, in both source water quality and treatment conditions, on the estimated health risks from microbiological contamination. Distribution system risks are not included in most QMRA models, and have not been included in this model. To ensure the model's accessibility to a large number of users, it has been developed using a widely available software platform (Microsoft Excel). Examples of other QMRA models that have been developed are provided in Box B1. Although it is widely accessible and relatively easy to use, the HC QMRA model still requires extensive knowledge and thoughtful considerations of the inputs that will be used on a site-specific basis. The initial data collection and on-site assessment of a water supply is a critical first step in applying the model successfully.
Box B1: Mathematical models for QMRA
Mathematical models have been developed by international organizations (U.S. EPA, 2005a, 2006a; Smeets et al., 2008; Teunis et al., 2009; Schijven et al., 2011, 2015), as well as by other groups within Canada (Barbeau et al., 2000; Jaidi et al., 2009; Pintar et al., 2012; Murphy et al., 2016), as a means to quantitatively assess the potential microbiological risks associated with a drinking water system. These models include potential risks associated with bacterial, protozoan and viral pathogens. Most models are not available in an easy to use, downloadable format. However, the QMRA model developed for regulatory use in the Netherlands (QMRAspot) can be downloaded and used by anyone interested in investigating the risks in their drinking water system (Schijven et al., 2011).
The first step in conducting a risk assessment is to define its scope by determining what questions need to be answered, and, therefore, what type of risk assessment is required. If it is determined that a quantitative risk assessment is needed, the HC QMRA model can be used as a screening level assessment, as well as an investigative tool to estimate risk ranges based on numerous scenarios, or to conduct a sensitivity analysis. The HC QMRA model does not provide an in-depth probabilistic assessment, where each component of the system is included as a stochastic element, and the level of uncertainty is reported. This level of assessment requires extensive knowledge of the specific water system being investigated and should be used only when the question being investigated requires an in-depth level of refinement. For example, if a screening level assessment, including scenario investigations, shows that the risks to human health are close to the health risk targets, further characterization of the system to better understand the variability and uncertainty may be warranted. If this level of analysis is required, an alternate model will be needed.
The HC QMRA model uses source water pathogen concentrations and treatment system information entered by the user, and ingestion and dose-response information for different microbial pathogens taken from the published literature. This information is used to estimate the daily and annual risk of infection, the annual risk of illness, and the disability adjusted life years (DALYs) per person per year associated with the input parameters. All four endpoints are displayed to allow comparison with not only the Health Canada target of 1 × 10−6 DALYs per person per year, but also with tolerable risk levels expressed using other metrics such as an annual risk of infection. An overview of the key model calculation steps are shown in Figure B1.

Figure B1 - Text Description
Figure 1 shows an overview of the key model calculation steps as: Pathogen concentrations in raw water; Log-reduction through treatment; Pathogen concentrations in treated water; Number of pathogens ingested per day; Annual health impacts in DALYs; Annual number of illnesses in the population; Probability of illness given infection; Annual number of infections in the population, and; Probability of infection given dose ingested.
The HC QMRA model aims to provide flexibility for users to analyze their drinking water systems in multiple ways. Users can input data that reflect their current drinking water systems, or can run scenarios to look at potential impacts of changes to various aspects of their drinking water system, such as changes in source water quality or modification of the type(s) of treatment applied. Model calculations are carried out using the mean values for most parameters, as opposed to using a more conservative estimate of the value, such as the 95th percentile. To capture the range of risk estimates that are possible in a water system, users should run multiple scenarios ranging from expected conditions to situations that represent conservative estimates. Scenario-based QMRAs using the HC model have been published (Hamouda et al., 2016; Bartrand et al., 2017a).
The HC QMRA model can be run using site-specific data, or using multiple assumptions and expert judgement for unknown parameters. Because of this flexibility, it is important to fully document the information that is being input into the model, including the basis of the information (e.g. monitoring data, referenced materials for assumptions, individual/team providing expert opinion, etc.). This provides the risk assessor with a better understanding of the uncertainty surrounding the data inputs to more accurately interpret the risk estimates that are obtained. Sections B.2 to B.5 provide an overview of the information to be entered into the HC QMRA model, considerations for obtaining this information, and the underlying assumptions and calculations being carried out to produce the disease burden estimates. Section B.6 includes example scenarios generated using model version - V15_05 Final.
B.2 Source water pathogen concentrations
The bacterial and protozoan reference pathogens used in this model are Cryptosporidium spp, Giardia lamblia, E. coli O157:H7, and Campylobacter spp. In the case of viruses, no one virus satisfied the criteria of a reference pathogen (see Box B2). Therefore, data from rotavirus, hepatitis A virus and poliovirus were used. These were selected after a careful review of candidate microorganisms.
Box B2: Reference pathogens
Although all enteric pathogens of concern to human health should be identified during a hazard assessment of a drinking water source, risk assessment models cannot consider each individual enteric pathogen. Instead, models include only specific enteric pathogens whose characteristics make them good representatives of a broader group of pathogens. These are referred to as reference pathogens. It is assumed that if the risk from the reference pathogens is reduced to a tolerable level, the risk from all pathogens in the broader group of pathogens will also be addressed. Ideally, a reference pathogen provides a conservative estimate of risk by representing a worst-case combination of high occurrence, high concentration and long survival time in source water, low removal and/or inactivation during treatment and a high pathogenicity for all age groups. Detection methods, preferably standardized methods, also need to be available for the reference pathogens chosen.
Cryptosporidium spp. and Giardia lamblia were selected as the reference protozoa. They are the enteric waterborne protozoa of most concern to human health in Canada. They have high prevalence rates, the potential to cause widespread disease, and pose a treatment challenge due to their resistance to chlorination. Also, dose-response models are available for both organisms.
Numerous enteric viruses have been considered as reference viruses, including adenoviruses, noroviruses, and rotaviruses. However, as no single virus has all the characteristics of an ideal reference virus, the risk assessment for enteric viruses uses characteristics from several different viruses. Since rotavirus is a common cause of infection, has been associated with severe outcomes, and has an available dose-response model, the virus risk assessment uses the health effect information from rotavirus but assumes that all age groups are susceptible to infection. Noroviruses are also a significant cause of viral gastroenteritis in all age groups, but there is still debate around the available published dose-response models (Schmidt, 2015). As such, norovirus has not been included in the model at this time, but will be considered for future updates. For drinking water treatment, adenoviruses represent the greatest challenge for inactivation when using UV, however, they are less prevalent in the human population. Consequently, the UV inactivation data from rotavirus was used. Data from hepatitis A virus and poliovirus was used for the chemical disinfectants (U.S. EPA, 1999) to reflect viruses that are more difficult to reduce during drinking water treatment. Due to limitations associated with available monitoring methods for enteric viruses, the concentration estimates in source water may also be based on total culturable enteric viruses, as opposed to only rotavirus.
E. coli O157:H7 and Campylobacter spp. were selected as the reference bacterial pathogens for this risk model for several reasons. They are responsible for both gastrointestinal illness and more serious health outcomes, have well established dose-response models, and are reduced through treatment at a similar level to other bacterial pathogens. In addition, Campylobacter spp. have high prevalence rates. Both pathogens are also of significant concern to human health in Canada. In addition, most drinking water utilities have data on total E. coli that can be used to estimate the concentration of E. coli O157:H7 in the source water, although this value will have a high level of uncertainty.
B.2.1 Determining source water quality
Where feasible, water providers are encouraged to implement a source water monitoring program that includes monitoring for reference pathogens, to provide site-specific information on the microbiological quality of the water. Further information on sampling methods for reference pathogens can be found elsewhere (Health Canada, 2019a,b). Pathogen monitoring information, along with the information obtained from the sanitary survey and faecal indicator monitoring, will help risk assessors provide the highest quality information to risk managers for drinking water decision making.
Developing an appropriate monitoring program will depend on site-specific characteristics of the source water and therefore monitoring plans may vary between locations. The goal of a monitoring program should be to sample for the organisms of interest to an extent and at a frequency that captures the most important sources of variation in microbiological source water quality. The low density of pathogens in many source waters and their episodic nature make this task difficult. Collected samples should be identified as either baseline (routine) samples or as event (incident) samples. Event samples are those collected during periods that are expected to adversely impact water quality such as flooding or storm events. Information that defines the sample as an event sample should be included so that the conditions that constituted the event are clear. This information can be used by risk assessors to help differentiate between baseline conditions and challenge periods, and investigate the impact that these water quality changes have on risk estimates.
Box B3: Pathogen monitoring frequencies
In the Netherlands, where a QMRA must be conducted at least every three years, surface waters are monitored for four reference pathogens: Cryptosporidium, Giardia, enteroviruses and Campylobacter. The monitoring frequency is based on the production volume of the plant and ranges from 9 to 35 samples in a three year period, including both routine and incident samples. All samples can be collected in a one year period to better capture variability (Schijven et al., 2011). In the United States, the Long-Term 2 Surface Water Treatment Rule required utilities to test their surface water sources for Cryptosporidium and Giardia to determine the level of treatment required. Samples were collected as close to the intake as possible, prior to treatment and either monthly for two years or bi-weekly for one year depending on the population being served and according to a pre-approved sampling schedule.
For many drinking water systems, it may not be feasible to obtain pathogen data for some or any of the reference pathogens in the model. Therefore, expert judgement can be used in place of the missing pathogen data. A broad range of individuals could provide expert judgement. Experts should have significant knowledge regarding the specific water supply to be able to make informed decisions regarding the sources and potential impacts of microbial pathogens. Expert judgement may be based on literature values from studies of similar types of water sources, or on unpublished data from surrounding water utilities, if available. It should take into consideration other site-specific information such as data from faecal indicators. Although faecal indicator data are not directly linked to pathogen concentrations, the typically larger datasets of faecal indicators can provide invaluable context for risk assessment regarding the magnitude and fluctuations of faecal contamination (WHO, 2016). This understanding can help risk assessors estimate the level of pathogens using data from literature sources. Sources of pathogen data that can be used by experts include the summaries of source water concentrations from Canadian watersheds published in Health Canada (2019a,b). Publications are also available with pathogen data from other countries (U.S. EPA, 2005b; Dechesne and Soyeux, 2007; Medema et al., 2009; Petterson et al., 2015; Health Canada, 2019b). Although they are not directly linked, some studies have used faecal indicator data to estimate pathogen concentrations. For example, E. coli monitoring data has been used, in combination with site-specific knowledge, to estimate Cryptosporidium concentrations for use in risk assessment (Medema et al., 2009; Hunter et al., 2011). It is important to note that pathogen concentration estimates based on indicator data or expert judgement will have a high degree of uncertainty, the scope and complexity of the risk therefore assessment being conducted need to be amenable to this approach. If a risk assessment is intended to produce precise quantitative answers, it would not be appropriate to use estimates.
One of the limitations of missing pathogen information is the tendency to use worse-case scenario assumptions, thus making concentration estimates more likely to overestimate risks. Overestimating risks can lead to costly decisions or the diversion of resources that could be better used elsewhere to protect public health. It is therefore important to include scenarios that represent the range of conditions that can be present, in addition to worst-case scenario assumptions. This should result in more informed answers to the questions laid out at the beginning of the risk assessment process. Using various scenarios, risk assessors can also determine which of the parameters have the greatest impact on the overall risk, and consequently provide some guidance on where the most benefit can be gained by reducing a parameter's uncertainty.
B.2.2 Estimating reference pathogen concentrations
Mean pathogen concentrations (per 100 L of water) and standard deviations are entered into the model and used to fit a lognormal distribution (see section B.2.3). Entering pathogen concentrations as arithmetic means and standard deviations were chosen to make the model accessible to a variety of users. When determining mean and standard deviations, risk assessors should consider how method recovery will be incorporated, and identify how non-detect data (i.e. samples where no organisms were detected in the volume analysed) will be included in the calculation. The model assumes that pathogens are randomly distributed in the water, and therefore does not account for clumping of organisms that can occurr in the water.
The recovery of the method is important because methods are never 100% efficient and the recovery efficiency is used to correct the pathogen concentration estimates. Collecting and analysing the large volume water samples needed to detect pathogenic microorganisms requires numerous steps. Each step in the method can contribute to the loss of some of the target organism, although occasionally recovery efficiency can also exceed 100%. Recovery efficiency can vary significantly between water matrices even with a standardized method, therefore, recovery efficiency would ideally be evaluated for each sample. It is recognized that this may not always be practical. For Cryptosporidium and Giardia datasets, most samples are analysed using U.S. EPA method 1622/23/23.1. This method includes requirements to determine the recovery in the water matrix being tested. The standard methods used for the other waterborne pathogens in the model do not have the same requirements, however, where possible, it is recommended that the recovery of these methods be assessed. In the absence of recovery efficiency information, the estimated pathogen recoveries will either have to be corrected using published literature values or assumed to be 100% (Schijven, 2011). For deterministic models, recovery is incorporated into risk models using a point estimate. In a stochastic model, it is usually assumed that the variability in recovery for a given method follows a beta distribution (Teunis et al., 1997; Makri et al., 2004; Pouillot et al., 2004; Signor and Ashbolt, 2006; U.S. EPA, 2014). Currently, the HC QMRA model does not include recovery. It assumes that the risk assessor has accounted for recovery (either with a point estimate or a stochastic approach) prior to entering the mean and standard deviation values.
Detection methods may not differentiate between viable human infective organisms and those that are not a human health risk, such as non-viable organisms or species that have never been associated with human infections. This could potentially overestimate the potential health impact. For example, for Giardia and Cryptosporidium detection, the routine method detects all (oo)cysts that are recovered, and it is assumed that all (oo)cysts detected in source waters are viable and equally infectious to humans, unless evidence to the contrary exists (e.g., genotyping results). For other reference pathogens, such as enteric viruses, standard methods based on cell culture detect infectious organisms but are difficult to carry out. Instead, molecular methods that do not differentiate between viable and non-viable organisms are often employed. If QMRA is used to help prioritize risk management decisions, overestimating the potential health impacts could lead to unneccesary expenditures. As such, where possible, assessing the viability and infectivity of the reference pathogens is recommended. The HC QMRA model allows the user to modify the fraction of infectious organisms when entering their source water pathogen data, however, the default value is 1.0 (i.e. all organisms are capable of causing infection) to provide a conservative estimate in the absence of other data.
Ideally, to get the best estimates of source water pathogen concentrations, the volume of sample analysed would be sufficient to have an average of at least 10 organisms in the sample (Emelko et al., 2008). However, in most source waters and for most pathogens, it is simply not feasible to collect and analyse the extremely large volume of water needed to recover an average of 10 organisms per sample. Because of this, pathogen datasets can contain a significant number of results with low pathogen counts and non-detect data. Although no organisms are recovered in non-detect samples, this does not mean that the source water contains no pathogens (i.e. they are not necessarily zero's). If a larger volume of water was analysed, or if the recovery efficiency of the method was better, it is possible that the pathogen would be detected. When calculating the mean and standard deviation, there are numerous approaches for including non-detect data in the calculation (see Box B4). Even in samples where pathogens are detected, the observed data is only an estimate of the concentration. To provide the best estimate of the concentration, measurement error would need to be considered (Schmidt and Emelko, 2011). However, accounting for measurement errors requires more complex calculations than those currently included in the HC model. Users need to decide how to include their non-detect data in the calculation of their estimated pathogen concentrations prior to calculating the mean and standard deviation for the water source.
Box B4: Transforming non-detect values
Numerous methods have been used in the literature to transform non-detect values into numerical values. The approach most commonly used for screening level risk assessments is to transform the non-detect values to numerical values by assuming they are all at a fixed concentration such as at the limit of detection (LOD), at ½ the LOD, or all zeros. Although this approach is very straightforward and simple, it will bias the concentration estimate. For example, assuming all non-detect samples have concentrations at the limit of detection could result in an overly conservative estimate of pathogen concentration. There are also statistical methods that can be used to transform non-detect data, such as maximum likelihood estimation or regression on order statistics. These methods use the data from samples with observed counts to estimate values for the non-detect data. The method chosen will impact the concentration estimate. For example, a study using UK finished water monitoring data transformed the below detection limit results using three different methods: all LOD values were assumed to be either all zeros (minimum values), at the LOD (maximum values), or were extrapolated linearly based on the positive detections (best estimate). It was shown that the risk varied by a factor of 4 (0.6 log) from the minimum to the maximum value assumptions (Smeets et al., 2007). The method chosen for transforming non-detection data will have a greater impact on risk estimates when overall pathogen concentrations are low (Smeets et al., 2007; Jaidi et al., 2009) and when datasets are small (Jaidi et al., 2009).
After deciding and documenting how non-detect data and method recovery efficiency will be addressed, mean and standard deviations can be calculated. There are many ways in which the same data can be analysed to estimate mean pathogen concentration and standard deviation parameters. The values could be the mean concentrations for each pathogen for a given year, to show a steady-state evaluation, or they could be the mean concentrations for each individual month to assess seasonal effects. Users can also enter concentrations from the range of values that may occur for any given scenario. This might include worst case values or defined values from the distribution of values such as the 75th or the 90th percentiles. A point estimate for the pathogen concentration can also be used by entering a very small standard deviation relative to the mean pathogen concentration (e.g., if mean = 1.0 organism /100 L, set standard deviation = 0.001 organisms/100 L).
The mean and standard deviations are entered on the Input_output worksheet of the model (see Figure B2). All pathogen concentrations, including E. coli, are entered in number of organisms per 100 L of water. The HC model estimates the concentration of pathogenic E. coli, using the total E. coli data from source water(s), by assuming a default value of 3.4% of the total E. coli detected is a pathogenic strain (Martins et al., 1992). This estimate is based on raw water samples collected from a blend of Colorado River and the Northern California Water project sources. This estimate will not represent all water sources and has a high level of uncertainty. Therefore, it is not a fixed value. It can be modified in the reference worksheet of the model to best reflect the source water quality being investigated. If a drinking water system has E. coli O157:H7 data and is entering this directly, the percentage of 3.4% will need to be changed to 100%. The input parameters and the corresponding results calculated by the model will need to be recorded elsewhere as the model does not store the data for the user.

Figure B2 - Text Description
A user input section of the HC QMRA model is displayed. The user has the option of entering data into the following input boxes: population; daily consumption (liters per day); and the mean, standard deviation, and fraction infectious for each of Cryptospordium, Giardia, rotavirus, Campylobacter, and E.coli. The user can also enter the value for the percent of E.coli that is E.coli O157.
B.2.3 Model calculations
Using the mean and standard deviation of the raw water pathogen concentrations entered on the Input_output worksheet, the model fits a log-normal distribution. The log-normal distribution uses the natural logarithm, and as it is not possible to take the natural logarithm of a zero value, a lognormal distribution cannot contain zero values. A log-normal distribution has the shape of a normal distribution (i.e., bell shape) when you take the natural logarithm of the variable (x), in this case, the raw water pathogen concentration. The model uses the arithmetic mean (μ) and standard deviation (σ) values that were entered on the Input_output worksheet, and then estimates the mean and standard deviation of ln(x), using the following equations:
(1)
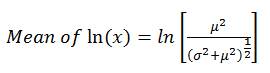
(2)
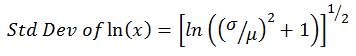
where,
- x = raw water pathogen concentration
- μ = mean pathogen concentration entered on Input_output worksheet
- σ = standard deviation entered on Input_output worksheet
The mean and standard deviation of ln(x) describes the shape of the lognormal distribution. The model divides the log-normal distribution curve into approximately 500 integration slices, each with an associated probability and mean concentration. This approach results in a weighted mean risk estimate. The probabilities were selected to divide the cumulative distribution function into equal segments (slices), totaling the entire area under the distribution curve. The exception is the initial portion of the curve, which is divided in smaller sections to provide better resolution at the low end of the distribution. For each integration slice, the model uses the probability for that slice and the inverse lognormal function to calculate the associated mean raw water concentration. The treated water concentration is then determined for each of the 500 slices based on the overall log-removal and log-inactivation achieved through treatment (see section B.3). The subsequent risk of infection is calculated for each slice based on the appropriate dose-response equation and is then multiplied by the probability associated with that slice of the distribution. The risk estimates are then summed to give the weighted mean risk of infection (see section B.4).
Box B5: Distributions for describing pathogen concentrations
Log-normal distributions are commonly used to describe the distribution of microorganisms in environmental samples (Westrell et al., 2003; Jaidi et al., 2009; Ongerth, 2013). They are used for a couple of reasons. First, the log-normal distribution is used for skewed data. This is often the situation with raw water pathogen data where there are a large number of samples at or near the LOD and a smaller number of high concentrations. Second, it has been shown to be a reasonable fit to source water concentration data (Smeets et al., 2008; Ongerth, 2013). Other distributions have been used in the literature, such as a gamma distribution, to describe environmental pathogen data (Schijven et al., 2011, 2015). Similar to the log-normal distribution, the gamma distribution is also used for skewed data and so may also fit the source water pathogen data. In reality, no distribution will fit observed data perfectly as distributions are simple approximations to a more complicated relationship. This means several different distributions may fit the observed data equally well and the choice of distribution is determined by the researchers involved.
B.3 Determination of treatment impacts
The treatment barriers in the QMRA model are separated into two types: (1) physical removal methods and (2) disinfection methods. An example of the input cells for the treatment barrier information can be found in Figure B3. Physical removals for each pathogen are expressed in terms of log10 removal, whereas disinfection is expressed as log10 inactivation. The determination of log reduction values are generally based on data from surrogate parameters at full-scale treatment, or by using bench- or pilot-scale studies with laboratory-adapted strains of the pathogens of interest. These reductions are assumed to be comparable to those occurring in the treatment plant. Pathogen removal data from full-scale treatment is not usually available for log reduction calculations since pathogen concentrations naturally occurring in source water are typically low and variable.

Figure B3 - Text Description
This figure displays both the user input section for the treatment barriers and operating conditions, and the summary of the treatment log-removal and log-inactivation values, from the HC QMRA model. The treatment barriers and operating conditions user input section provides the following options: a drop down menu of options for coagulation; a drop down menu of options for filtration; a drop down menu of options for disinfection #1; a drop down menu of options for disinfection #2; input boxes for contact time in minutes, baffle factor in T10 over T, initial concentration in mg/L, decay factor k (per min), temperature in degrees Celsius, and pH for each of disinfection #1 and #2; a drop down menu of options for disinfection #3, with an input box for UV dose in mJ per cm2. Two graphs are also displayed in this section, representing the disinfection information input by the user for disinfection #1 and #2. Each graph displays the hydraulic residence time in minutes on the x-axis and there are two y-axes, disinfection residual in mg/L and CDF (from 0 to 1). This section also includes 2 output boxes that display a baffle factor check and the calculated N-CSTR. The second section of this figure displays the summary of treatment log-removal and log-inactivation for each of Cryptosporidium, Giardia, rotavirus, Campylobacter, and E.coli O157. The values displayed reflect the treatment barriers and operating conditions selected by the user. The overall log reduction and the standard deviation (based on the physical removal information) are also displayed.
B.3.1 Physical removal methods
The physical removal options are separated into a coagulation step (Log RemC&S) and a filtration step (Log RemFiltr.) to provide more flexibility in representing a treatment system. The coagulation steps are the following:
- coagulation only;
- coagulation and flocculation;
- coagulation, flocculation and sedimentation;
- none; or
- user specified.
The filtration methods are:
- rapid granular (no coagulation);
- rapid granular (inline coagulation / direct filtration);
- rapid granular (with coagulation/sedimentation);
- slow sand;
- membrane (micro);
- membrane (ultra);
- none; or
- user specified.
For the coagulation steps, the only selection that provides log removals is the coagulation/flocculation/sedimentation option. The remaining coagulation processes do not have a particle removal step and therefore, their contributions to removals are considered part of the filtration step. Thus, for conventional treatment, both coagulation/flocculation/sedimentation and granular filtration (with coagulation/sedimentation) need to be selected to represent full conventional treatment. For drinking water treatment systems that use dissolved air flotation, the removals provided for coagulation/flocculation/sedimentation are considered a reasonable estimate of this process.
The log removal data incorporated into the model for these treatment processes are based on published literature. With the exception of membrane filtration removals, the data included for each treatment stage are the weighted mean values taken from a large literature survey (Hijnen and Medema, 2007). To determine the weighted mean values for each treatment process, the authors used a weighting factor, on a scale of 1 to 5 based on the quality of the study, to calculate the weighted average log removals. For example, studies that were conducted at full-scale were given higher weight than pilot-scale studies, and studies that used pathogens as opposed to surrogates were also given greater weight. For membrane filtration, an arithmetic mean and standard deviation were calculated based on the available studies; no weighting factors were applied. The table of literature values can be found in the Treatment worksheet of the model. These data can be modified to update new pilot and full-scale research results as they become available.
As indicated by the literature values, the range of log removals associated with a treatment type can vary by up to 6 orders of magnitude depending on treatment conditions. Treatment processes that have not been optimized, or that are experiencing suboptimal performance, may not be achieving the default log removal values included in the model. There are numerous factors that can impact the log removal capability of filtration processes, and these will vary with the type of filtration. Some of these factors include source water quality, filtration rates, effective chemical pretreatment, filter media size/type, filter condition, filter run length, filter maturation, water temperature, filter integrity and backwashing procedures. The level of variability in treatment performance emphasizes the importance of understanding the treatment system that is being assessed. Further information on filtration and pathogen removals can be found in Health Canada (2013b). As mentioned previously, one of the main advantages of using a QMRA approach is that it requires on-site evaluation of the water supply system. Relying on the literature values included in the model may underestimate or overestimate the performance at a specific site. This needs to be considered by risk assessors and risk managers when making drinking water management decisions.
The option of specifying log removal/inactivation values, as opposed to using literature values, is available by selecting "user specified" and then defining the mean log-removals and standard deviation for each of the reference pathogens (Cryptosporidium, Giardia, rotavirus, E. coli, and Campylobacter). This is done in the Treatment worksheet of the model. As log reductions can vary even in well operated treatment plants, it is better to have site specific information whenever possible (Smeets et al., 2007) to be used in place of the literature values. This option is very useful for treatment plants that have carried out extensive in-house monitoring and consequently have reliable pathogen removal data demonstrating that their system performs differently than what is published in the literature. This option also provides the opportunity to investigate improvements possible through process optimization, or conversely, the impact of conditions such as suboptimal coagulation or end of filter run conditions. However, in many treatment plants, site-specific information will not be available and the drinking water system will need to rely on the pre-determined log reduction values in the model.
B.3.2 Disinfection methods
The model includes seven options:
- free chlorine;
- chloramines;
- ozone;
- chlorine dioxide;
- ultraviolet (UV) disinfection;
- none; and
- user specified.
The model allows for two stages of chemical disinfection (Log InactDisinf1 and Log InactDisinf2). To calculate the log inactivation for the chemical disinfectants (free chlorine, chloramines, ozone and chlorine dioxide), six parameters must be entered to describe the disinfection process (see Figure B3):
- contact time (min);
- baffle factor (T10/T);
- initial disinfectant concentration (mg/L);
- disinfectant decay factor (min−1);
- pH; and
- temperature (°C).
For UV disinfection, only the UV effective dose or fluence (mJ/cm2) needs to be entered for the treatment plant. Numerous factors can impact the dose delivered, including the hydraulic profile within the reactor, flow rate, the UV transmittance of the water, UV intensity, lamp output, lamp placement, and lamp aging and fouling (U.S. EPA, 2006b; Bolton and Cotton, 2008), and these should be considered before entering data into the model. As mentioned earlier, the log inactivation equations have generally been developed using laboratory adapted strains of pathogens. This adds some uncertainty to the calculations since environmental strains may not respond in exactly the same manner as laboratory strains.
The model uses the six parameters (listed above) and a continuously stirred tank reactors (N-CSTR) approach for the CT inactivation calculations of all the chemical disinfectants (details below). This approach was chosen to provide a more accurate estimate of the log inactivation being achieved in a full-scale disinfectant contact basin. This was especially important for ozone inactivation because of the fast decay rates associated with this disinfectant.
B.3.2.1 CT inactivation calculations
For chemical disinfection, the model uses segregated flow analysis to estimate the overall pathogen inactivation achieved within the contact basin. In this method, the water volume entering the contact basin is divided into 1000 segments or "slices" based on the residence time distribution (RTD). The log-inactivation for each flow segment is calculated individually using the disinfectant concentration, disinfectant decay factor, pH, and temperature. These individual slices are then summated over the entire basin to determine the overall log-inactivation. By taking into account all segments of water entering the basin, including portions that short-circuit through the basin quickly and portions that are detained longer, a more accurate estimate of pathogen inactivation is obtained. It is important to note that the pathogen inactivation calculated by the model will not match values obtained using the conservative T10 method commonly used for regulatory and operational purposes.
Since most treatment plants do not have a detailed RTD, the model uses an N-CSTR approach (see Box B6 for details). The RTD is determined based on two user-specified values: the contact time (also referred to as the hydraulic retention time) T, and the baffle factor, defined by T10/T. Both of these parameters are usually known for a given treatment plant since they are commonly used to determine pathogen inactivation from published CT tables.
The hydraulic retention time T (in minutes) is calculated by V/Q, the volume of water V (m3) in the basin divided by the volumetric flowrate Q (m3/min) passing through. This represents the overall retention time of fluid in the basin, recognizing that some water will pass quickly through the basin while other portions will be retained longer.
The baffle factor (T10/T) is a dimensionless ratio that characterizes the relative spread of retention times for a given basin. The T10 value represents the time at which 10% of the influent has passed through the basin in comparison to the overall hydraulic retention time T. Baffle factors range between 0 and 1 with a low value (eg. 0.1) for dispersed flow with short-circuiting and a high value (eg. 0.9) representing nearly "plug-flow" conditions. Most treatment plant contact basins have baffle factor values in the range of 0.3 to 0.7. Baffle factor values can be accurately measured using chemical tracer studies (Teefy, 1996) or estimated based on the geometry of the contact chamber. Descriptions of basin layout are available to help guide water system operators estimate their baffle factors based on their system characteristics. These descriptions and additional information can be found in U.S. EPA (2003) and MOE (2006) documents.
The initial disinfectant concentration and the disinfectant decay factor are used by the QMRA model to provide a decreasing concentration profile based on 1st order decay kinetics. Most CT calculations by water system operators assume a fixed concentration of chemical disinfectant throughout the contact chamber. However, the approach used in the model better reflects operating conditions in actual treatment plants and provides a more accurate estimate of pathogen inactivation. For users who do not know their decay factor, it can be estimated using the following equation:
(3)
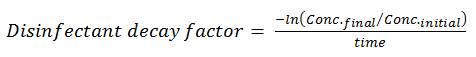
The initial concentration of disinfectant (Conc.initial) is the concentration (mg/L) remaining following the immediate oxidant demand. The final concentration of disinfectant (Conc.final) is the concentration (mg/L) after the contact time has elapsed, and time is the contact time (min). In general, decay factors tend to fall in the range of 0.001 to 0.2 min−1 depending on water characteristics and the chemical disinfectant being used. The disinfectant decay factor can be assessed using jar studies or plant measurements, or can be determined through trial and error knowing the residual concentration profile through the basin. The user can enter a value and review the corresponding residual profile displayed to the right (see Figure B3). Once the outlet disinfectant residual matches observed operating conditions, the estimated disinfectant decay factor is reasonable. Alternatively, for a more conservative estimate of log inactivation, the user can enter their final disinfectant concentration as their initial concentration and set the decay factor to 0 to maintain the final disinfectant concentration through all the CSTR calculations.
Box B6: The N-CSTR approach
The distribution or spread of retention times in a contact chamber can be represented mathematically by a number of theoretical CSTR (Continuous Stirred Tank Reactors) operating in series. At the extreme ends, contact basins can range from fully mixed or dispersed (=1 CSTR) to nearly "plug-flow" condition (eg. long pipe) represented by an infinite number of CSTRs in series. Contact basins in treatment plants fall somewhere between these two extremes. An equation developed by Nauman and Buffham (1983) relates a number of "N" CSTRs as a function of the baffle factor T10/T, providing an estimated residence time distribution for the contact basin. The resulting residence time distribution is divided into 1000 integration 'slices'. The chemical inactivation is calculated individually for each 'slice' using CT disinfection equations. The disinfectant concentration for each integration 'slice' is estimated from the initial concentration and the decay factor resulting at time t. The remaining fraction of organisms is calculated for each 'slice' and then summated over the entire basin to calculate the overall fraction of organisms remaining following the disinfection process. Further details on the N-CSTR calculations can be found elsewhere (Bartrand et al., 2017b)
B.3.3 Overall treatment reduction
Once the log-removal and log-inactivation credits are determined for the treatment processes, the overall log-reduction for each specific pathogen is calculated by adding the log removal/inactivation credits for the various treatment steps.
(4)
LogRed Treat = LogRemC&S + LogRemFiltr + LogInactDisinf1 + LogInactDisinf2
A summary of the log removal and inactivation values is displayed on the Input_output worksheet of the model (see Figure B3). The model also displays the treatment reduction by barrier for each of the reference pathogens in a bar graph (not shown). The overall log-reduction is then used to determine the concentration of each reference pathogen in the treated drinking water.
B.4 Dose-response calculations
The goal of the dose-response calculation is to estimate the probability of infection associated with a drinking water source. To do this, the model uses the average doses of the five reference pathogens, calculates the probability of ingesting discrete doses (between 0 and 100 organisms) given the average dose, and finally uses numerical integration to estimate the probability of infection. This process is described in detail below.
B.4.1 Determining pathogen dose
As mentioned in section B.2, the model assumes that the raw water pathogen concentration data follows a log-normal distribution. The model divides this distribution into more than 500 integration slices to represent the total range of the distribution curve. For each of the slices, the model estimates the source water pathogen concentration and uses the overall treatment reduction to determine the treated drinking water concentration for each integration slice, as follows:
(5)
Pathogen ConcTreated = Pathogen ConcSource × 10−Treatment Log Reduction
The mean dose of pathogens that may be consumed by an individual is then calculated for each of the potential treated water concentrations described by the log-normal distribution, as follows:
(6)
Dose IngestedDay = Pathogen ConcTreated × Water ConsumptionDay
The model default for average water consumption per day (Water ConsumptionDay) is 1.0 L of unboiled tap water. In a population, there will be a distribution of consumption values that are not captured by this point estimate (Statistics Canada, 2004, 2008). Data from the recent surveys of water use in Canada is included in the Reference worksheet of the model. Although the default value is 1.0 L, this value can be modified on the Input_output worksheet to reflect populations with alternative average consumptions (Figure B2).
B.4.2 Determining the probability of infection
The probability of infection is calculated using the dose-response model and parameters for each pathogen, as shown in Table B1. The exponential model has been chosen for Cryptosporidium and Giardia, whereas the beta-Poisson model is used for rotavirus, E. coli O157:H7, and Campylobacter.
| Pathogen | Dose response model | Constants | Reference |
|---|---|---|---|
| Cryptosporidium | Exponential | r = 0.018 | (Messner et al., 2001) |
| Giardia | Exponential | r = 0.01982 | (Rose and Gerba, 1991) |
| Rotavirus | Beta-Poisson | α = 0.265 β = 0.4415 |
(Haas et al., 1999) |
| E. coli O157 :H7Footnote 1 | Beta-Poisson | α = 0.0571 β =2. 2183 |
(Strachan et al., 2005) |
| Campylobacter | Beta-Poisson | α = 0.145 β = 7.59 |
(Medema et al., 1996) |
|
|||
Box B7: Dose-reponse models
Dose-response models are developed based on feeding trials, outbreak investigations, or a combination of the two. There are numerous models that could be used to describe the results from the dose-response studies, however, the models that have been shown to best describe the observed data are either the exponential model or the beta-Poisson model. Both the exponential and the beta-Poisson models are based on the single-hit theory, that is, each organism acts independently of one another and only one organism needs to survive the host-pathogen interaction in order to initiate an infection (Haas et al., 1999).
B.4.2.1 Exponential model (for Cryptosporidium and Giardia)
The exponential model has two main assumptions underlying its derivation. Firstly, it assumes that the number of pathogens initiating an infection is binomially distributed and that the response is the same if a single pathogen, or more than one pathogen, is responsible for the infection. Based on this assumption, the probability of at least one pathogen resulting in an infection, given a known discrete number of pathogens, can be determined using the following equation:
(7)
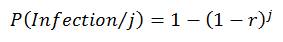
In this equation, j is an exact discrete number of pathogens and r is a pathogen specific constant derived from dose-response studies (Table B1).
Secondly, the exponential model assumes that the probability of ingesting an exact discrete dose of organisms (j) given an average concentration of pathogen consumed per day from drinking water (Dose Ingestedday) can be described by the following equation (i.e., a Poisson distribution):
(8)
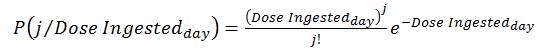
In the HC QMRA model, discrete numbers of pathogens (j) ranging from no organisms up to a maximum of 100 organisms, in increments of 1 additional organism per dose, are used. The product of equations (7) and (8) results in the probability of infection for the parameters entered. Section B.4.3 describes how these probabilities are used.
B.4.2.2 Beta-Poisson model (for rotavirus, E.coli O157:H7, Campylobacter)
The derivation of the beta-Poisson model is similar to that of the exponential model except that the beta-Poisson model assumes that the probability of a known exact number of pathogens (j) not eliciting a response is beta-binomially distributed, as opposed to binomially distributed. Therefore, the probability of a least one pathogen resulting in an infection, out of a known number of pathogens, can be determined using the following equation:
(9)
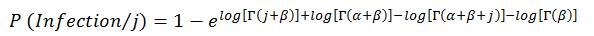
where,
- α and β are pathogen specific parameters used to describe the ability of the pathogen to survive and initiate infection in an individual, derived from dose-response studies (Table B1); and
- Γ represents a gamma function; log is the natural logarithm.
The second assumption of the beta-Poisson model is the same as for the exponential model: that the actual dose ingested by an individual is Poisson distributed and can be described by equation (8). The product of equations (8) and (9) results in the probability of infection for the parameters entered. An approximation to the beta-Poisson model is often used in the literature as it simplifies the equation. It was not used in this model as the assumptions for its use were not met by the reference pathogens selected. However, due to limitations of the selected software platform (Microsoft Excel), the exact beta-Poisson model (containing the Kummer confluent hypergeometric function) could not be included. Instead, the beta-Poisson model was decomposed into its beta-bionomial and Poisson distributions as decribed above. Section B.4.3 describes how the infection probabilities are used.
B.4.3 Probability of infection
The dose-response calculations in section B.4.2 determine the probability of infection for each slice of the log-normal distribution at each discrete dose between 0 and 100 organisms. This approach (i.e. a conditional dose-reponse approach) was employed due to limitations of the selected software platform when using complex dose-response models such as the exact beta-Poisson model. This results in a large data matrix that needs to be summed by the model to provide a final probability of infection. First, for each slice of the lognormal distribution, the model calculates the probability of ingesting each discrete dose (from 0 to 100) given the mean number of organisms ingested for that slice. The probability of ingestion is then multiplied by the corresponding probability of infection and subsequently summed, to give the probability of infection for a slice of the log-normal distribution. This is done for each of the approximately 500 integration slices from the lognormal distribution. Each distribution slice is then weighted using the probability of the pathogen concentration occurring from the log-normal distribution. The weighted probabilities of infection are then summed to give the overall probability of infection per day (Pinfection,day). This value is displayed on the Input_Output worksheet (see Figure B4).
In an effort to reduce model running times, the limit of 100 organisms was applied as a compromise between realistic Canadian drinking water source contamination and treatment scenarios. It is expected that the concentration of any given pathogen in treated drinking water in Canada should be well below 100 organisms per litre as an average dose. Since the discrete dose upper limit was set at 100 organisms, this model cannot be used to examine scenarios where the average ingested dose is greater than this value. For example, if a user enters data that represents a drinking water source where there is no treatment and the source water is highly contaminated such that the average pathogen dose ingested is above 100, the model will incorrectly estimate very low probabilities of infection and illness because the concentration of pathogens is outside of the analysis range. Such a scenario raises a flag in the model to alert the user.

Figure B4 - Text Description
The output results for the HC QMRA model are displayed. This includes the following calculated values for each of Cryptospordium, Giardia, rotavirus, Campylobacter, and E.coli: the daily probability of infection for an individual; the probability of infection per year for an individual; the probability of illness per year for an individual; the total number of illnesses per year in the population; the DALY’s per 1000 cases of illness, presented as the YLD, the LYL, and the total contribution (respectively); the annual DALY risk for an individual; and the total number of DALY’s per year in the population.
The following equation is used to calculate the probability of 1 or more infections per year, given a daily risk of infection (Pinfection, day) (WHO, 2016):
(10)
Pinfection per year = 1 − (1 − Pinfection, day)365
This equation assumes that the risk of infection is the same every day for the entire year and that there is no resistance or immunity acquired in the population. In reality, the risk of infection will vary from day to day based on changes in source water quality, treatment efficiency and volume of water consumed. In addition, previous infection with some enteric pathogens provides protective immunity from subsequent infections. Although equation (10) provides a good estimate of the average annual probability of infection, it may overestimate the range of the probabilities of infection since infection risk is assumed the same every day (Petterson et al., 2015). However, the purpose of the HC QMRA model is not to predict the number of infections or illnesses in a population, but to provide a probability that disease may occur based on the source water quality and treatment system information. The above assumptions are considered reasonable for the purposes of examining relative risks in a system.
B.5 Estimating health impacts
The final step in the HC QMRA model is to determine the burden of disease, expressed in DALYs, associated with the input scenario for each of the reference pathogens. DALYs are used in this risk assessment model as a common metric to compare illnesses with different health endpoints. It is also used to allow comparisons to an established health target, in this case, the reference level of 10−6 DALYs per person per year. The calculated burden of disease values are displayed on the Input_Output worksheet (see Figure B4).
B.5.1 Determining probability of illness
To determine the disease burden for each reference pathogen, it is necessary to calculate the probability of becoming ill, given that infection has occurred, as not all infections lead to illness. Some infected individuals may clear the infection without ever having developed any symptoms. Others might be asymptomatic carriers of the infection. These individuals also have no symptoms, but they do continue to shed the pathogen in their feces.
The probability of illness given infection (Pill/inf) varies with each reference pathogen. The values used by the model for Pill/inf are based on the published literature and are given in Table B2. They are also found in the Reference worksheet of the model. For E. coli O157:H7, the dose-response model estimates the probability of illness, so Pill/inf is 1.0 for the risk calculations. For Campylobacter, current studies do not provide a consistent value for the Pill/inf. The relationship seems to be dose dependent, with some doses showing a Pill/inf of 1.0. However, further studies are needed. In the interim, the Pill/inf has also been set at 1.0 as a conservative estimate.
| Pathogen | P(ill/inf) | Reference |
|---|---|---|
| Cryptosporidium | 0.70 | Casmen et al., 2000 |
| Giardia | 0.40 | Nash et al., 1987 |
| Rotavirus | 0.88 | Havelaar and Melse, 2003 |
| E. coli O157:H7 | 1.0 | Strachan et al., 2005 |
| Campylobacter | 1.0 | Assume all infections lead to illness |
The probability of illness per year for an individual (Pillness,yr) is calculated using the following equation. This calculation is carried out for each of the 5 reference pathogens.
(11)
Pillness, yr = Pinfection per year × Pill/inf
The total number of illnesses in a population can be calculated for each pathogen by multiplying the annual risk of illness times the population.
(12)
Illnesses per yearpop = Pillness, yr × Population
B.5.2 Calculating DALYs
Although estimating the probability of illness per person per year is informative, it does not provide a clear indication of the health burden associated with the drinking water source as the magnitude of the health impacts vary for each reference pathogen. DALYs are used as a common metric to compare illnesses with different health endpoints. DALY's include life-years-lost (LYL) to calculate the impact of premature death due to illness, as well as years lived with a disability (YLD) to calculate the morbidity associated with an illness.
B.5.2.1 Calculating LYL
Since premature death eliminates potential years of healthy living, the LYL is calculated as the difference between the age at death and the full life expectancy for the population, multiplied by the severity weight associated with loss of life and the fraction of ill individuals who experience the outcome (referred to as the outcome fraction).
(13)
LYL = (life expectancy − age at death) × severity weight × outcome fraction
The model uses the combined life expectancy (i.e. the average of male and female life expectancies - 80.88 years)(Statistics Canada, 2012), as the reference pathogens do not have gender specific health outcomes. For Cryptosporidium, Giardia, rotavirus, and E.coli O157, the weighted median age (38.98 years) is used as the age at death. This assumes that there is no difference in fatality rates between the age categories. For Campylobacter, death primarily occurs in the elderly population. Therefore, the age at death is assumed to be the median age of the eldest population category (72.94 years). Complete tables of life expectancy and age values for the Canadian population can be found in the Reference worksheet of the model. In all instances, a severity weight of 1.0 is assigned for loss of life. Table B3 provides the severity weights and outcome fraction information for each reference pathogen. The outcome fractions for death are assumed to be 1 in 100,000 for Cryptosporidium and Giardia. Rotavirus and Campylobacter are assumed to have a case fatality ratio of 1 in 10,000. For E.coli O157:H7, the risk of death is higher, at 1 in 4,000 (Havelaar and Melse, 2003).
B.5.2.2 Calculating YLD
To calculate the years lived with a disability (YLD), the outcome fraction is multiplied by the severity weight (Table B3) and the duration of the illness (Table B4) for each illness outcome that is attributed to the pathogen. These products are then summed to give the YLD per case of illness.
(14)
YLD per case = Σ Outcome fraction(duration of illness × severity weight)
| Illness outcome | Severity weightFootnote e | Outcome fractions | ||||
|---|---|---|---|---|---|---|
| CryptosporidiumFootnote c | GiardiaFootnote a | RotavirusFootnote a | CampylobacterFootnote b | E.coli O157Footnote b | ||
| Mild diarrhea | 0.067 | 0.99999 | 0.99999 | 0.50 | 1.00 | 0.53 |
| Bloody diarrhea | 0.39 | 0.50 | 0.06 | 0.47 | ||
| Guillain-Barré syndrome (GBS) clinical and residual |
0.0002 | |||||
| GBS; residual | 0.0002 | |||||
| Reactive arthritis | 0.023 | |||||
| hemolytic uremic syndrome (HUS) | 0.93 | 0.01000 | ||||
| end-stage renal disease (ESRD) | 0.95Footnote d | 0.00118 | ||||
| Death (GBS) | 1.0 | 0.0000046 (1 in 217,000) |
||||
| Death | 1.0 | 0.00001 (1 in 100,000) |
0.00001 (1 in 100,000) |
0.0001 (1 in 10,000) |
0.0001 (1 in 10,000) |
0.00025 (1 in 4,000) |
|
||||||
| Illness Outcome | Cryptosporidium | Giardia | Rotavirus | Campylobacter | E.coli O157 |
| mild diarrhea | 0.01918 (7 days) |
0.01918 (7 days) |
0.01918 (7 days) |
0.01397 (5.1 days) |
0.00932 (3.4 days) |
| serious diarrhea (i.e., bloody) | - | - | 0.01918 (7 days) |
0.0230 (8.4 days) |
0.01534 (5.6 days) |
| HUS | - | - | - | - | 0.0575 (21 days) |
| ESRD | - | - | - | - | 9.35 |
| clinical (GBS) residual (GBS) reactive arthritis |
0.29Footnote a 5.8Footnote a 0.115 (42 days) |
||||
| death (GBS) death |
(e* - adeath) | (e* - adeath) | (e* - adeath) | (e* - adeath) (e* - adeath) |
(e* - adeath) |
|
|||||
B.5.2.3 Total DALYs
The total DALYs per case of illness is the sum of the YLD and the LYL. In the case of a waterborne pathogen causing mild gastrointestinal illness and having a low-case fatality ratio, it is common to see the disease burden expressed in terms of DALYs per 1000 cases to illustrate the health impact more clearly. Figure B4 shows the estimated DALYs per case of illness for each of the reference pathogens including the contribution from morbidity (YLD) and mortality (LYL). With the exception of rotavirus, these DALY values are very similar to comparable values reported in the literature (Gibney et al., 2014). The DALYs per 1000 cases calculated using this model for rotavirus are approximately three times greater than the study in the literature due to differing assumptions made surrounding the susceptible population and the duration of illness.
The DALYs per person per year is then calculated by multiplying the probability of illness per person per year by the DALYs per case of illness for each pathogen. These values can then be compared to the health target of 1 × 10−6 DALYs per person per year as recommended in the Guidelines for Canadian Drinking Water Quality. The DALYs per person per year (annual DALY risk [individual]) are displayed on the Input_output worksheet of the model (Figure B4). The model also displays the total DALYs per year in the population based on the population that is added by the user on the Input_Output worksheet.
B.6 Using the model - an illustrative example
The following sections present a brief example of how the QMRA model can be used. This example is not intended to provide a step-by-step procedure for conducting a risk assessment using the model. It is a simplified approach, included for illustrative purposes only, to show how the QMRA model can help make risk management decisions in a drinking water system. Other examples of risk assessments can be found elsewhere (U.S. EPA, 2005a, 2006a; Medema et al., 2009; Schijven et al., 2011; WHO, 2016; Bartrand et al., 2017a,b).
B.6.1 Scope of the risk assessment
The municipal drinking water system in this fictional case study is supplied by a surface water treatment plant that draws raw water from a large river and supplies water to a population of 200,000. The municipality has been conducting pathogen monitoring for two years on a monthly basis (details below). The samples were collected on a pre-set schedule. The sampling conditions (i.e., baseline or incident) were not recorded. With their dataset of pathogen monitoring results, and information on the treatment processes in place, the municipality wants to conduct a screening level risk assessment to determine where they fall in relation to the tolerable risk level of 1 × 10−6 DALYs per person per year (baseline risk estimate). In addition, the municipality would like to investigate how that risk level could be impacted by (1) challenging water conditions, (2) altering a disinfection barrier under baseline and challenging conditions (3) losing a treatment barrier for a period of time, as well as (4) the effectiveness of using an alternative physical removal method. These analyses will be part of the evidence used to help support upcoming decisions surrounding modifications to, and future expansions of, the current treatment system.
The system will use the pathogen monitoring data it has collected to estimate mean and standard deviations for each of the reference pathogens. As there is no site-specific information on pathogen log reductions, the literature values from the model will be used. The route of exposure is assumed to be only through the ingestion of unboiled tap water with an average per capita consumption of 1.0 litre of unboiled tap water per day.
B.6.2 Baseline risk estimate
The watershed surrounding the river is largely wilderness, and the river generally has low turbidity (3-5 NTU), high colour (35 true colour units) and dissolved oxygen content (6.5 mg/L). There are only a few small communities upstream of the city, with minimal wastewater discharges. Large numbers of waterfowl (Canada geese, gulls and shorebirds) can be found on the river during migration, and some overwinter in areas that do not freeze completely. A few major tributaries drain agricultural areas, which may contribute both nutrients and pathogens from animal waste to the river. Monitoring data for various pathogens in raw water were collected over two years. The data sets for all pathogens, with the exception of E.coli, contained samples that were below the LOD for the method. All below LOD samples were included in the concentration estimates assuming the concentrations were at the LOD. They were also corrected for recovery based on information received from the laboratory (when available).
The pathogen concentrations did not have clear seasonal trends, and since the samples where not identified as baseline or incident samples, the data from the two years of monitoring (24 samples) was combined into a single mean and standard deviation estimate (Table B5). These estimates, although they do capture variability in the pathogen concentrations, will still have uncertainty arising from the limited number of samples taken, and from limitations in pathogen detection methods, including determining whether the pathogens are human infectious. However, for the purposes of the scenarios being investigated by the utility, the uncertainty in these values will not be further explored.
| Pathogen | Cryptosporidium (no./100 L) |
Giardia (no./100 L) |
Rotavirus (no./100 L) |
Campylobacter (cfu/100 mL) |
E.coli (cfu/100 mL) |
|---|---|---|---|---|---|
| Mean | 8.0 | 34.0 | 56.0 | 10.0 | 55.0 |
| Standard deviation | 12.0 | 72.0 | 62.0 | 22.0 | 100.0 |
| cfu = colony-forming unit | |||||
The water treatment plant has a conventional treatment process that includes: coarse screening, coagulation, flocculation, sedimentation, dual-media filtration, chlorine disinfection (primary disinfection), pH adjustment and chloramination (secondary disinfection). It is assumed that there is no further treatment or disinfection of the tap water prior to consumption, and that the quality of the treated water does not deteriorate in the distribution system.
Physical removal performance for the treatment process is not known, so the weighted mean average efficiencies for coagulation/sedimentation and filtration - rapid granular (with coagulation/sedimentation) from the QMRA model will be used. The values for these two steps are added to give the overall log removal. Using the values from the QMRA model will add uncertainty to the estimated risks, as site-specific log removals could be orders of magnitude different from the average values included in the model. However, as a screening assessment, the utility decided that average values from the literature were acceptable for the scenarios they wanted to investigate.
For primary disinfection, the chlorine residual immediately following the initial demand is 0.50mg/L followed by a 60-minute contact time (pH=6.0, temperature=10°C). The contact time is based on mean detention time, rather than the T10 value, as this assessment is aimed at estimating the mean reduction through the treatment process. The contact basins have been properly constructed to minimize short circuiting and the baffle factor has been determined to be 0.65. The disinfectant decay factor for chlorine in this system is 0.002.
Using the QMRA model and the log reductions shown in Table B6, the mean burden of disease estimates for the reference pathogens were calculated (Table B7). The distribution of the estimates is shown in Figure B5. Levels of illness in this range would not reasonably be detected and, with the exception of the extreme tail of Giardiasis, are well below the reference level of risk of 10−6 DALYs/person per year.

Figure B5 - Text Description
A graph showing the distribution of the annual burden of illness estimates from the consumption of drinking water produced using baseline treatment conditions. The distribution of the burden of illness estimates are shown for each of Cryptosporidium, Giardia, rotavirus, Campylobacter, and E. coli O157:H7. The x-axis of the graph is the risk expressed as DALYs per person per year. It is presented on a logarithmic scale and the axis values range from 10−15 to 1. The y-axis of the graph is the normalized probability distribution function. It is presented on a linear scale and the axis values range from 0 to 1. The reference level of risk of 10−6 DALYs per person per year is illustrated on the graph as a dotted vertical line. The annual illness estimates for each pathogen are normally distributed. The distribution curves extend approximately from: slightly less than 10−10 to 10−7 for Cryptosporidium; slightly more than 10−11 to 10−6 for Giardia; slightly less than 10−14 to slightly more than 10−11 for rotavirus; 10−13 to slightly more than 10−9 for Campylobacter, and slightly more than 10−13 to almost 10−8 for E. coli O157:H7. The peak of each probability distribution is normalized to 1.
B.6.3 Treatment barrier modifications
Using the same pathogen data (Table B5), the QMRA model was used to investigate how modifying the treatment barriers might affect the quality of the water being produced. The QMRA model calculates risk estimates based on annual exposure, therefore the model assumes that the values used occur in the system each day for the entire year. Although a constant daily risk is unlikely to occur, as water quality and treatment performance will vary throughout the year, this assumption allows the comparison of treatment scenarios (i.e., an investigation of relative risks). This value is also used for comparison to tolerable health risk targets. The model also displays the daily individual risk of infection. The daily risk of infection can be used to investigate the relative risks of short-term treatment disruptions. The fictional system in this scenario wanted to investigate the impact of the following potential treatment variations as separate scenarios: (1) effectiveness of chlorine disinfection during challenging conditions (i.e., cold water temperatures and reduced contact time), (2) loss of chlorine disinfection for an extended period of time (e.g. 2 hours), (3) implementation of ozone as an alternative disinfectant to chlorine and (4) effectiveness of a membrane filtration plant in comparison to conventional treatment.
For the first scenario, the QMRA model inputs were set to represent challenging disinfection conditions. The water temperatures in the system fluctuate from 1°C to 21°C throughout the year. The system relies on chlorine for disinfection of pathogens, and the inactivation rates for this chemical are temperature dependent. Therefore, the QMRA model was run using the same parameters as the baseline estimate, with the following modifications: the temperature of the water was set to 1°C and the contact time used was 20 minutes to represent a conservative estimate for chlorine inactivation. The log reductions under these conditions are show in Table B6. The calculated health risks are shown in Table B7. Since chlorine inactivation is ineffective against Cryptosporidium, the challenging disinfection conditions have no impact on the reduction of this pathogen through treatment. Conversely, the bacterial pathogens are highly susceptible to inactivation by chlorine. Therefore, even using the conservative estimates, the maximum inactivation applied by the model (>8.0 log) is still achieved. The greatest impact on estimated risk is from Giardia and rotavirus. The estimated risk from Giardia increased by approximately 1 log and the annual estimated risk for rotavirus increased by approximately 1.7 log. Both are still below the annual target, although Giardia is now within one order of magnitude and further investigation to determine the uncertainty around the log reductions being achieved may be warranted.
| Process (log10) | Cryptosporidium | Giardia | Rotavirus | Campylobacter | E. coli |
|---|---|---|---|---|---|
| Baseline conditions | |||||
| Coagulation/Sedimentation | 1.86 | 1.61 | 1.76 | 1.55 | 1.55 |
| Filtration - Rapid granular (with coag/sed) | 2.41 | 1.92 | 1.11 | 0.87 | 0.87 |
| Chlorine inactivation (10°C, 60 min) |
0.0 | 1.15 | > 8.0 | > 8.0 | > 8.0 |
| Modified treatment | |||||
| Chlorine inactivation (1°C, 20 min) |
0.0 | 0.23 | 6.3 | > 8.0 | > 8.0 |
| Ozone inactivation (10°C, 20 min) |
0.25 | 4.0 | 4.0 | 8.0 | 8.0 |
| Ozone inactivation (1°C, 20 min) |
0.10 | 3.79 | 4.0 | 8.0 | 8.0 |
| Membrane filter (microfiltration) | 6.13 | 6.62 | 1.10 | 4.60 | 4.60 |
| Chlorine failure (only physical removal) | 4.27 | 3.53 | 2.87 | 2.42 | 2.42 |
For the second scenario, the fictional utility wanted to investigate the increased level of risk associated with a short-term complete loss of chlorine disinfection. A time-frame of 2 hours was chosen to represent the amount of time for a chlorine loss to be discovered and corrected. It was assumed that the pathogens present in the 2 hours of unchlorinated water were evenly dispersed in the distribution system and were mixed with the remaining chlorinated water produced for that day. This simulates the entire population being exposed to the pathogens released during the chlorine failure, but at a diluted concentration. An alternative approach would be to assume that the 2 hours of unchlorinated water remain undispersed and therefore a smaller number of people would be exposed to a much higher level of pathogens. However, the former approach provides a more conservative estimate since exposing the entire population (albeit at the diluted concentration) will result in a greater DALY burden as more people are likely to get ill, compared to exposing a smaller number of people to a high concentration of pathogens. In order to calculate the short-term risk, the daily risk of infection was used, as opposed to the annual health risk. First, the treated water concentrations for both the baseline condition and the chlorine failure condition were calculated for each pathogen using equation (5) along with the source water concentration and treatment reduction information from Table B5 and B6. Next, the calculated treated water concentrations for the baseline (CB) and chlorine failure (CCF) were used to estimate the overall diluted concentration (CD) of each reference pathogen in the treated water (equation (15)).
(15)
CD = CB(22hr/24hr) + CCF(2hr/24hr)
The treated water concentration (CD) for each reference pathogen was then input as the mean raw water concentration on the input screen of the HC model and all treatment selections were set to none, since a treated water concentration is being used. The standard deviation was maintained at the original values. The daily probability of infection calculated for this scenario is shown in Table B7. By comparing the daily probability of infection between this scenario and the baseline values, it is evident that the loss of the chlorine disinfection for 2 hours has a large impact on the daily risks from viruses, Campylobacter and E. coli. In a population of 200,000, this increase in risk would theoretically result in 4, 61, and 20 infections, respectively. By comparison, the treated water produced under baseline conditions would result in 0.0001, 0.0005, and 0.0008 respectively (i.e. negligible). This information led the utility to further investigate the impacts of loss of chlorine over different timeframes to inform criticial control point decisions (not shown).
For the third scenario, the fictional utility wanted to investigate the use of an alternative primary disinfectant, in this case, ozone. For this scenario, it was assumed that coagulation/sedimentation and filtration were unchanged; however, the primary disinfectant being added was ozone, as opposed to chlorine. Both baseline and challenging water conditions were considered for comparison. The ozone concentration immediately following the initial demand was projected to be 0.50 mg/L followed by a 20-minute contact time [pH = 6.0, temperature = 10°C (baseline) or 1°C (challenging)]. Since ozone is known to react very quickly in water, the contact time was set at the T10 value for both scenarios. The baffle factor was still 0.65. The disinfectant decay factor for ozone in this system was assumed to be 0.2.
The mean burden of disease estimates are shown in Table B7. The distribution of the estimates (for the baseline conditions) is shown in Figure B6. For the challenging water quality conditions, the mean burden of disease estimates for Cryptosporidium and Giardia were the only estimates that changed, with the estimated risk increasing by approximately 0.1 and 0.2 log, respectively. The utility then used the estimated ozone log reduction values for cold water to compare to the baseline chlorine disinfection estimates. This comparison showed that the estimated risk from Cryptosporidium, Campylobacter, and E.coli O157:H7 remained approximately the same. A very low level of inactivation of Cryptosporidium occurred when using ozone (0.1 log), compared to none with chlorine. The maximum inactivation allotted by the model was achieved for both of the reference bacteria, as they are highly susceptible to both disinfectants. Giardia, on the other hand, were more easily inactivated with ozone and so the estimated risk decreased by approximately 3 log. Conversely, the estimated risk from rotavirus increased by approximately 4 log, however, based on available published studies, the model caps the log inactivation using ozone at 4 log less than for chlorine (which is capped at 8 log) making direct comparison difficult. All of the estimated risks were below the annual health target.

Figure B6 - Text Description
A graph showing the distribution of the annual burden of illness estimates from the consumption of drinking water produced using ozone disinfection under baseline treatment conditions. The distribution of the burden of illness estimates are shown for each of Cryptosporidium, Giardia, rotavirus, Campylobacter, and E. coli O157:H7. The x-axis of the graph is risk in DALYs per person per year. It is presented on a logarithmic scale and the axis values range from 10−15 to 1. The y-axis of the graph is the normalized probability distribution function. It is presented on a linear scale and the axis values range from 0 to 1. The reference level of risk of 10−6 DALYs per person per year is illustrated on the graph as a dotted vertical line. The annual illness estimates for each pathogen are normally distributed. The distribution curves extend approximately from: slightly less than 10−10 to almost 10−6 for Cryptosporidium; slightly less than 10−13 to 10−9 for Giardia; slightly more than 10−10 to slightly less than 10−6 for rotavirus; 10−13 to slightly more than 10−9 for Campylobacter, and slightly more than 10−13 to almost 10−8 for E. coli O157:H7. The peak of each probability distribution is normalized to 1.
In the fourth scenario, the fictional utility wanted to investigate the use of an alternative physical removal process as part of a future water treatment plant expansion project. For this scenario, it was assumed that chlorine disinfection was occurring under the conditions of the baseline estimates (10°C, 60 min) for the current plant. The alternative physical removal process was assumed to be microfiltration (Table B6). The mean burden of disease estimates are shown in Table B7. The distribution of the estimates is shown in Figure B7. With the exception of rotavirus, the microfiltration scenario resulted in estimated risks equivalent to, or lower than, the conventional treatment plant. Rotavirus risks were greater but still well below the annual health target.
| Scenario/brief description | Cryptosporidium | Giardia | Viruses | Campylobacter | E. coli | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| DALYs / p·yr | Pinf, daily | DALYs/ p·yr | Pinf, daily | DALYs/ p·yr | Pinf, daily | DALYs/ p·yr | Pinf, daily | DALYs/ p·yr | Pinf, daily | |
| Baseline | 3.3 × 10−8 | 7.6 × 10−8 | 3.6 × 10−8 | 1.5 × 10−7 | 7.6 × 10−12 | 2.9 × 10−12 | 1.2 × 10−10 | 7.4 × 10−11 | 1.6 × 10−10 | 1.8 × 10−11 |
| 1/ 1°C, 20 min | 3.3 × 10−8 | 7.7 × 10−8 | 3.0 × 10−7 | 1.2 × 10−6 | 3.8 × 10−10 | 1.4 × 10−10 | 1.2 × 10−10 | 7.4 × 10−11 | 1.6 × 10−10 | 1.8 × 10−11 |
| 2/ 2 hour chlorine loss | N/A | 5.5 × 10−8 | N/A | 2.1 × 10−7 | N/A | 2.0 × 10−5 | N/A | 3.0 × 10−4 | N/A | 1.0 × 10−6 |
| 3/ Ozone, 10°C | 1.9 × 10−8 | 4.4 × 10−8 | 5.0 × 10−11 | 2.0 × 10−10 | 7.6 × 10−8Footnote * | 2.9 × 10−8Footnote * | 1.3 × 10−10 | 7.4 × 10−11 | 1.6 × 10−10 | 1.8 × 10−11 |
| 3/ Ozone, 1°C | 2.6 × 10−8 | 6.1 × 10−8 | 8.1 × 10−11 | 3.3 × 10−10 | 7.6 × 10−8Footnote * | 2.9 × 10−8Footnote * | 1.3 × 10−10 | 7.4 × 10−11 | 1.6 × 10−10 | 1.8 × 10−11 |
| 4/ Membrane filtration | 4.5 × 10−10 | 1.1 × 10−9 | 2.9 × 10−11 | 1.2 × 10−10 | 4.5 × 10−10 | 1.7 × 10−10 | 8.3 × 10−13 | 4.9 × 10−13 | 1.1 × 10−12 | 1.2 × 10−13 |
|
||||||||||

Figure B7 - Text Description
A graph showing the distribution of the annual burden of illness estimates from the consumption of drinking water produced using membrane filtration as per scenario 3. The distribution of the burden of illness estimates are shown for each of Cryptosporidium, Giardia, rotavirus, Campylobacter, and E. coli O157:H7. The x-axis of the graph is the annual DALY risk in DALYs per person per year. It is presented on a logarithmic scale and the axis values range from 10−15 to 1. The y-axis of the graph is the normalized probability distribution function. It is presented on a linear scale and the axis values range from 0 to 1. The reference level of risk of 10−6 DALYs per person per year is illustrated on the graph as a dotted vertical line. The annual illness estimates for each pathogen are normally distributed. The distribution curves extend approximately from: slightly more than 10−12 to slightly more than 10−8 for Cryptosporidium; slightly more than 10−14 to slightly more than 10−9 for Giardia; slightly more than 10−12 to slightly more than 10−9 for rotavirus; 10−9 for Campylobacter, and slightly more than 10−15 to almost 10−10 for E. coli O157:H7. The peak of each probability distribution is normalized to 1.
B.6.4 Interpreting risk estimates
Using the QMRA scenarios in this case study, the drinking water treatment plant appears to be producing drinking water of an acceptable microbiological quality, assuming that the conditions entered into the QMRA model are reflective of the drinking water system. From the treatment reductions applied in the model (Table B6), it is clear that the log reductions attributable to the physical removal processes are essential in controlling the risk from Cryptosporidium. Chlorine and ozone under the conditions entered offer negligible inactivation. Giardia, on the other hand, is reduced by both physical removal and disinfection. However, under challenging disinfection conditions, such as chlorine disinfection in cold water, the risk from Giardia may be approaching the target level based on the data entered in the model. This result should prompt this fictional utility to conduct some further investigation to better characterize the probable risk from Giardia to determine whether the system is meeting their health targets under all water conditions. For the bacterial and viral pathogens (Campylobacter, E.coli O157:H7 and rotavirus), disinfection is the main barrier for reducing these organisms to acceptable levels. In the event of a sustained failure in chlorine disinfection, such as in scenario 2, the daily risk from the bacterial and viral pathogens was greatly increased. Using the results from scenario 3, it was noted that viral pathogens are more resistant to disinfection than bacterial pathogens. The challenging water conditions with chlorine disinfection led to a probability of risk that was almost 2 orders of magnitude greater than the baseline conditions, albeit still well below the tolerable risk level. However, ozone disinfection appeared to be unaffected by the lower temperature used for this case study. Ozone was also more effective for controlling the risks from Giardia. Scenario 4 for this fictional utility, investigating the use of microfiltration as opposed to conventional filtration, showed that under the conditions of the model, microfiltration could be used to produce acceptable water quality.
The above scenarios show the relative impact on pathogen reductions based on the input parameters and the assumptions used. Understanding the assumptions made in the model is key to properly interpreting the results of the scenarios. For example, the scenario for this fictional utility assumes that the utility's physical removal processes are achieving the weighted mean log removals reported in the literature. These may over- or underestimate the log reductions being achieved by several orders of magnitude. Although this is an example of an assumption that could have a large impact on the scenario results, other parameters have less variability and therefore would have very little impact. Understanding these impacts is part of interpreting the results from the scenarios investigated. The above scenarios would be used as a starting point for the fictional utility to run further analyses that explore the range of impacts that could be expected by altering the treatment performance. The utility may also want to explore further the variability in the pathogen concentrations to determine the impact on the estimated risks. The relative risk levels could then be used to help support decisions on alternative treatment processes, or to determine what input parameters would benefit from further exploration into their site-specific variability to reduce some of the uncertainty in the results.
Part C. References and acronyms
C.1 References
Ashbolt, N.J., Schoen, M.E., Soller, J.A. and Roser, D.J. (2010). Predicting pathogen risks to aid beach management: The real value of quantitative microbial risk assessment (QMRA). Water Res., 44(16): 4692-4703.
Barbeau, B., Payment, P., Coallier, J., Clément, B. and Prévost, M. (2000). Evaluating the risk of infection from the presence of Giardia and Cryptosporidium in drinking water. Quant. Microbiol., 2(1): 37-54.
Bartrand, T.A., Hargy, T., McCuin, R. and Rodriguez del Rey, Z. (2017a). Demonstration of the Health Canada quantitative microbial risk assessment tool for two drinking water plants in the United Kingdom. Water Research Foundation, U.S.A.
Bartrand, T.A., Hargy, T., McCuin, R., Rodriguez del Rey, Z., Douglas, I., Elliot, J., Andrews, R. and McFadyen, S. (2017b). Using QMRA to estimate health risks of pathogens in drinking water. Water Research Foundation, U.S.A.
Bolton, J.R. and Cotton, C.A. (2008). The ultraviolet disinfection handbook. American Water Works Association, Denver, Colorado.
Casman, E.A., Fischhoff, B., Palmgren, C., Small, M.J. and Wu, F. (2000). An integrated risk model of a drinking-water - borne cryptosporidiosis outbreak. Risk Anal., 20(4): 495-511.
Dechesne, M. and Soyeux, E. (2007). Assessment of source water pathogen contamination. J. Water Health, 5 Suppl 1: 39-50.
Emelko, M.B., Schmidt, P.J. and Roberson, J.A. (2008). Quantification of uncertainty in microbial data - reporting and regulatory implications. J. Am. Water Works Assoc., 100(3): 94-104.
Gibney, K.B., O'Toole, J., Sinclair, M. and Leder, K. (2014). Disease burden of selected gastrointestinal pathogens in Australia, 2010. Int. J. Infect. Dis., 28: e176-e185.
Haas, C.N., Rose, J.B. and Gerba, C.P. (1999). Quantitative microbial risk assessment. John Wiley & Sons, Inc, New York, New York.
Hamouda, M.A., Anderson, W.B., Van Dyke, M.I., Douglas, I.P., McFadyen, S.D. and Huck, P.M. (2016). Scenario-based quantitative microbial risk assessment to evaluate the robustness of a drinking water treatment plant. Water Qual. Res. J. Can., 51(2): 81-96.
Havelaar, A.H. and Melse, J.M. (2003). Quantifying public health risk in the WHO Guidelines for drinking-water quality: a burden of disease approach. Rijkinstituut voor Volskgezondheid en Milieu, RIVM 734301022, Bilthoven, The Netherlands.
Health Canada (2013a). Guidance on the use of the microbiological drinking water quality guidelines. Water and Air Quality Bureau, Healthy Environments and Consumer Safety Branch, Health Canada, Ottawa, Ontario. Available at: www.canada.ca/en/health-canada/services/environmental-workplace-health/reports-publications/water-quality/guidance-use-microbiological-drinking-water-quality-guidelines-health-canada-2013.html
Health Canada (2013b). Guidelines for Canadian drinking water quality: Guideline technical document - turbidity. Health Canada, Ottawa, Ontario Canada. Available at: https://www.canada.ca/en/health-canada/services/publications/healthy-living/guidelines-canadian-drinking-water-quality-turbidity.html.
Health Canada (2019a). Guidelines for Canadian drinking water quality: Guideline technical document - enteric protozoa: Giardia and Cryptosporidium. Water, Air and Climate Change Bureau, Healthy Environments and Consumer Safety Branch, Health Canada, Ottawa, Ontario. Available at: www.canada.ca/en/health-canada/services/environmental-workplace-health/reports-publications/water-quality/enteric-protozoa-giardia-cryptosporidium.html.
Health Canada (2019b). Guidelines for Canadian drinking water quality: Guideline technical document - enteric viruses. Health Canada, Ottawa, Ontario. Available at: www.canada.ca/en/health-canada/services/publications/healthy-living/guidelines-canadian-drinking-water-quality-guideline-technical-document-enteric-viruses.html
Hijnen, W.A.M. and Medema, G. (2007). Elimination of micro-organisms by drinking water treatment process: A review. Kiwa Water Research, Nieuwegein, The Netherlands.
Hunter, P.R., De Sylor, M.A., Risebro, H.L., Nichols, G.L., Kay, D. and Hartemann, P. (2011). Quantitative microbial risk assessment of cryptosporidiosis and giardiasis from very small private water supplies. Risk Anal., 31(2): 228-236.
Jaidi, K., Barbeau, B., Carrière, A., Desjardins, R. and Prévost, M. (2009). Including operational data in QMRA model: Development and impact of model inputs. J. Water Health, 7(1): 77-95.
Macler, B.A. and Regli, S. (1993). Use of microbial risk assessment in setting US drinking water standards. Int. J. Food Microbiol., 18(4): 245-256.
Makri, A., Modarres, R. and Parkin, R. (2004). Cryptosporidiosis susceptibility and risk: A case study. Risk Anal., 24(1): 209-220.
Martins, M.T., Rivera, I.G., Clark, D.L. and Olson, B.H. (1992). Detection of virulence factors in culturable Escherichia coli isolates from water samples by DNA probes and recovery of toxin-bearing strains in minimal o-nitrophenol-ß-D-galactopyranoside-4-methylumbelliferyl-ß-D- glucuronide media. Appl. Environ. Microbiol., 58(9): 3095-3100.
Medema, G., Teunis, P., Blokker, M., Deere, D., Davison, A., Charles, P., and Loret, J-F. (2009). Risk assessment of Cryptosporidium in drinking water. WHO Press, World Health Organization, Geneva, Switzerland.
Medema, G.J., Teunis, P.F.M., Havelaar, A.H., Haas, C.N. (1996). Assessment of the dose-response relationship of Campylobacter jejuni. Int. J. Food Microbiol., 30: 101-111.
Messner, M.J., Chappell, C.L. and Okhuysen, P.C. (2001). Risk assessment for Cryptosporidium: A hierarchical bayesian analysis of human dose response data. Water Res., 35(16): 3934-3940.
MOE (2006). Procedure for disinfection of drinking water in Ontario as adopted by reference by Ontario regulation 170/03 under the safe drinking water act. Ontario Ministry of the Environment, PIBS 4448e01, Toronto, Ontario.
Murphy, H.M., Thomas, M.K., Medeiros, D.T., McFadyen, S. and Pintar, K.D.M. (2016). Estimating the number of cases of acute gastrointestinal illness (AGI) associated with Canadian municipal drinking water systems. Epidemiol. Infect., 144(7): 1371-1385.
Murray, C. and Lopez, A. (1996a). Global health statistics. Harvard School of Public Health, Cambridge, Massachusetts.
Murray, C.J.L. and Lopez, A.D. (1996b). The global burden of disease: A comprehensive assessment of mortality and disability from disease, injury and risk factors in 1990 and projected to 2020. Harvard University Press, Cambridge, Massachusetts.
Nash, T.E., Herrington, D.A., Losonsky, G.A. and Levine, M.M. (1987). Experimental human infections with Giardia lamblia. J. Infect. Dis., 156(6): 974-984.
Nauman, E.B., and Buffham, B.A. (1983). Mixing in continuous flow systems. Wiley, New York.
Ongerth, J.E. (2013). ICR SS protozoan data site-by-site: A picture of Cryptosporidium and Giardia in U.S. surface water. Environ. Sci. Technol., 47(18): 10145-10154.
Petterson, S., Roser, D. and Deere, D. (2015). Characterizing the concentration of Cryptosporidium in Australian surface waters for setting health-based targets for drinking water treatment. J. Water Health, 13(3): 879-896.
Petterson, S.R. and Ashbolt, N.J. (2016). QMRA and water safety management: Review of application in drinking water systems. J. Water Health, 14(4): 571-589.
Pintar, K.D.M., Fazil, A., Pollari, F., Waltner-Toews, D., Charron, D.F., Mcewen, S.A. and Walton, T. (2012). Considering the risk of infection by Cryptosporidium via consumption of municipally treated drinking water from a surface water source in a southwestern Ontario community. Risk Anal., 32(7): 1122-1138.
Pouillot, R., Beaudeau, P., Denis, J. and Derouin, F. (2004). A quantitative risk assessment of waterborne cryptosporidiosis in France using second-order Monte Carlo simulation. Risk Anal., 24(1): 1-17.
Rose, J.B. and Gerba, C.P. (1991). Use of risk assessment for development of microbial standards. Water Sci. Technol., 24(2): 29-34.
Schijven, J., Derx, J., de Roda Husman, A.M., Blaschke, A.P. and Farnleitner, A.H. (2015). QMRAcatch: Microbial quality simulation of water resources including infection risk assessment. J. Environ. Qual., 44(5): 1491-1502.
Schijven, J.F., Teunis, P.F.M., Rutjes, S.A., Bouwknegt, M. and de Roda Husman, A.M. (2011). QMRAspot: A tool for quantitative microbial risk assessment from surface water to potable water. Water Res., 45(17): 5564-5576.
Schmidt, P.J. (2015). Norovirus dose-response: Are currently available data informative enough to determine how susceptible humans are to infection from a single virus? Risk Anal., 35(7): 1364-1383.
Schmidt, P.J. and Emelko, M.B. (2011). QMRA and decision-making: are we handling measurement errors associated with pathogen concentration data correctly? Water Research, 45: 427-438.
Signor, R.S. and Ashbolt, N.J. (2006). Pathogen monitoring offers questionable protection against drinking-water risks: A QMRA (quantitative microbial risk analysis) approach to assess management strategies. Water Sci. Techol. 54(3): 261-268.
Signor, R.S. and Ashbolt, N.J. (2009). Comparing probabilistic microbial risk assessments for drinking water against daily rather than annualised infection probability targets. J. Water Health, 7(4): 535-543.
Smeets, P.W.M.H., van Dijk, J.C., Stanfield, G., Rietveld, L.C. and Medema, G.J. (2007). How can the UK statutory Cryptosporidium monitoring be used for quantitative risk assessment of Cryptosporidium in drinking water? J. Water Health, 5(SUPPL. 1): 107-118.
Smeets, P.W.M.H., Dullemont, Y.J., Van Gelder, P.H.A.J.M., Van Dijk, J.C. and Medema, G.J. (2008). Improved methods for modelling drinking water treatment in quantitative microbial risk assessment; a case study of Campylobacter reduction by filtration and ozonation. J. Water Health, 6(3): 301-314.
Soller, J.A. and Eisenberg, J.N.S. (2008). An evaluation of parsimony for microbial risk assessment models. Environmetrics, 19(1): 61-78.
Statistics Canada (2004). Data source: Canadian community health survey, cycle 2.2 - nutrition (wave 3): General health and 24-hour dietary recall. (Share File). Statistics Canada, Ottawa, Ontario.
Statistics Canada (2008). User guide: Canadian community health survey (CCHS), cycle 2.2 (2004), nutrition - general health (including vitamin & mineral supplements) & 24-hour dietary recall components. Statistics Canada, Ottawa, Ontario.
Statistics Canada (2012). Life table, Canada, provinces and territories 2007-2009. Ministry of Industry, ISBN: 978-1-100-21498-6.
Strachan, N.J.C., Doyle, M.P., Kasuga, F., Rotariu, O. and Ogden, I.D. (2005). Dose response modelling of Escherichia coli O157 incorporating data from foodborne and environmental outbreaks. Int. J. Food Microbiol., 103(1): 35-47.
Teefy, S. (1996). Tracer studies in water treatment facilities: a protocol and case studies. Water research Foundation, Denver, CO.
Teunis, P.F.M., Medema, G.J., Kruidenier, L. and Havelaar, A.H. (1997). Assessment of the risk of infection by Cryptosporidium or Giardia in drinking water from a surface water source. Water Res., 31(6): 1333-1346.
Teunis, P.F.M., Rutjes, S.A., Westrell, T. and de Roda Husman, A.M. (2009). Characterization of drinking water treatment for virus risk assessment. Water Res., 43(2): 395-404.
U.S. EPA (1999). Disinfection profiling and benchmarking guidance manual. U.S. Environmental Protection Agency, Washington, DC (Report No. EPA/815/R-99/013).
U.S. EPA (2003). LT1ESWTR disinfection profiling and benchmarking technical guidance manual. Office of Water, U.S. Environmental Protection Agency, Washington, DC.
U.S. EPA (2005a). Economic analysis for the final Long Term 2 Enhanced Surface Water Treatment Rule. U.S. Environmental Protection Agency, EPA 815-R-06-001.
U.S. EPA (2005b). Occurrence and exposure assessment for the final Long Term 2 Enhanced Surface Water Treatment Rule. Office of Water, EPA 815-R-06-002,.
U.S. EPA (2006a). Economic analysis for the final Groundwater Rule. U.S. Environmental Protection Agency, EPA 815-R-06-014.
U.S. EPA (2006b). Ultraviolet disinfection guidance manual. Office of Water, U.S. Environmental Protection Agency, Washington, DC (Report No. EPA/815/R-06/007).
U.S. EPA (2014). Microbiological risk assessment (MRA) tools, methods, and approaches for water media. Office of Water, Office of Science and Technology. U.S. Environmental Protection Agency, EPA-820-R-14-009, Washington, DC.
WHO (2004). Guidelines for drinking-water quality. 3rd edition. World Health Organization, Geneva, Switzerland.
WHO (2016). Quantitative microbial risk assessment: Application for water safety management. World Health Organization, Geneva, Switzerland.
Westrell, T., Bergstedt, O., Stenström, T.A. and Ashbolt, N.J. (2003). A theoretical approach to assess microbial risks due to failures in drinking water systems. Int. J. Environ. Health Res., 13(2): 181-197.
C.2 Acronyms
- CSTR
- continuously stirred tank reactor
- CT
- concentration × time
- DALYs
- disability adjusted life years
- EPA
- Environmental Protection Agency (U.S.)
- ESRD
- end-stage renal disease
- GBS
- Guillain-Barré syndrome
- HC
- QMRA Health Canada quantitative microbial risk assessment (model)
- HUS
- hemolytic uremic syndrome
- LOD
- limit of detection
- LYL
- life years lost
- QMRA
- quantitative microbial risk assessment
- RTD
- Residence time distribution
- UV
- ultraviolet
- WHO
- World Health Organization
- YLD
- years lived with a disability
- UV
- ultraviolet