Sélection de la langue

Gouvernement du Canada / Government of Canada

Recherche

Comment déterminer la masse volumique du métal – Notes de l’Institut canadien de conservation (ICC) 9/10

Introduction

La masse volumique est la masse d’un objet divisée par son volume. Elle est caractéristique du matériau dont est fait un objet, qu’elle contribue d’ailleurs à identifier.

Sauf s’il est de forme simple, il est difficile de déterminer directement le volume d’un objet. Un moyen facile de déterminer la masse volumique d’un objet en métal est de le peser dans l’air, puis de le peser une fois immergé dans un liquide, comme il est expliqué dans la section Aspects scientifiques du calcul de la masse volumique. L’eau est le liquide le plus pratique, mais si l’objet ne peut être immergé dans l’eau, on utilise un solvant organique, comme l’éthanol ou l’acétone. La masse volumique de l’objet se calcule à partir des deux mesures de masse et de la masse volumique du liquide.

Avec une balance appropriée et un contenant de la bonne taille, on utilisera cette méthode sur une variété d’objets, petits ou gros, métalliques ou non. Elle fonctionne avec des objets de forme complexe, et même les objets percés, pourvu que le liquide puisse pénétrer dans les trous et les remplir. Une fois la masse volumique déterminée, on la compare avec celle de matériaux connus afin de limiter les possibilités quant à la composition de l’objet. 

La présente Note décrit la procédure à suivre et le matériel nécessaire pour déterminer la masse volumique d’un objet en métal. La première étape consiste à appliquer la procédure à un ou à plusieurs objets en métal de composition connue – soit un métal pur ou un alliage – afin d’expérimenter et de s’assurer d’utiliser correctement la procédure. On déterminera ensuite la masse volumique d’un objet en métal de composition inconnue.

Procédure : comment déterminer la masse volumique d’un objet en métal

Équipement et matériel requis pour déterminer la masse volumique

  • Petits objets métalliques qu’on peut immerger dans l’eau
  • Balance à dispositif de pesée sous le socle (c’est-à-dire que les objets peuvent être suspendus sous la balance) à précision minimale de 0,01 gramme (voir la section Balance sans dispositif de pesée sous le socle pour adapter la méthode afin de peser sous la balance)
  • Fil métallique à fixer au crochet installé dans la balance (un trombone déplié et recourbé aux deux extrémités fait parfaitement l’affaire)
  • Plateforme ou support sur lequel déposer la balance pour pouvoir suspendre des objets en dessous à l’aide du crochet
  • Bécher assez grand pour y immerger complètement les objets sans que le liquide déborde
  • Support pour maintenir les béchers à la bonne hauteur sous la balance
  • Eau du robinet
  • Calculatrice  
  • Fil de nylon (par exemple, fil à pêche ou matériau léger équivalent) pour suspendre les objets sous la balance
  • Gants jetables en nitrile
  • Facultatif : serre-joints pour fixer le support de la balance au bord d’un comptoir

Marche à suivre pour déterminer la masse volumique à l’aide d’une balance à dispositif de pesée sous le socle

  1. Retirer la plaque d’ouverture sous le socle de la balance pour exposer le crochet qui se trouve à l’intérieur.
  2. Poser la balance sur un support percé donnant accès au crochet intérieur.
  3. Fixer un crochet métallique au crochet intérieur, puis mettre la balance à zéro.
  4. Suspendre un objet au crochet situé sous la balance à l’aide d’un fil de nylon ou équivalent et le peser dans l’air. Porter des gants pour manipuler des objets en métal, surtout s’il y a lieu de penser qu’ils renferment du plomb.
  5. Remplir le bécher d’eau et le déposer sous la balance.
  6. Soulever le bécher jusqu'à ce que l'objet soit complètement immergé. Placer un support sous le bécher pour le maintenir à la bonne hauteur. S’assurer qu’aucune bulle d’air n’est piégée sous l’objet ni dans les vides à l’intérieur de l’objet.
  7. Peser l’objet immergé.
  8. Calculer sa masse volumique au moyen de l’équation ci-après.
  9. Comparer la masse volumique calculée avec la masse volumique connue d’autres métaux et alliages à l’aide du tableau ci-après ou des listes plus complètes fournies dans les références.
  10. Répéter les étapes 4 à 9 avec les autres objets.

Comment calculer la masse volumique

La masse volumique ρ d’un objet ou d’un matériau se définit comme la masse m divisée par le volume V, soit la formule ρ = m/V. Si l’objet est pesé dans l’air afin de déterminer sa masse réelle et pesé dans un liquide pour déterminer sa masse apparente, sa masse volumique s’exprime alors par l’équation :


La masse volumique de l’eau est de 0,998 g/cm3 à 20 °C et de 0,997 g/cm3 à 25 °C.

Résultats de la procédure

Exemples d’objets

La figure 1 montre huit exemples d’échantillons faits de divers métaux utilisés pour illustrer la procédure.

Objets en métal utilisés pour illustrer la méthode.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0358
Figure 1. Objets en métal utilisés pour illustrer la procédure.

Voici la liste des objets présents dans la figure 1 avec, entre parenthèses, leur masse volumique calculée :

Du coin supérieur gauche vers la droite :

  1. probablement de la fonte grise (7,13 g/cm3)
  2. aluminium de grande pureté (2,70 g/cm3)
  3. alliage de cuivre rougeâtre (peut-être 85 % de cuivre et 15 % de zinc : 8,23 g/cm3)
  4. cuivre de grande pureté (8,88 g/cm3);

Du coin inférieur gauche vers la droite :

  1. zinc moulé (alliage inconnu : 7,09 g/cm3)
  2. plomb de grande pureté (11,20 g/cm3)
  3. étain de grande pureté (7,27 g/cm3)
  4. laiton jaune à cartouche (70 % de cuivre et 30 % de zinc : 8,45 g/cm3)

La masse volumique de chaque objet a été déterminée à l’aide de la formule susmentionnée. Ainsi, dans le cas de l’objet en aluminium (b), la masse était de 110,18 g dans l’air et de 69,45 g dans l’eau, ce qui donne une masse volumique de 2,70 g/cm3. Pour l’objet en fonte (a), la masse était de 209,47 g dans l’air et de 180,13 g dans l’eau, soit une masse volumique de 7,13 g/cm3. Pour l’objet en plomb (f), la masse était de 102,44 g dans l’air et de 93,31 g dans l’eau, soit une masse volumique de 11,20 g/cm3.

Les masses volumiques mesurées de l’aluminium, de la fonte et du plomb (2,7, 7,13 et 11,20 g/cm3) sont proches des masses volumiques connues répertoriées dans le tableau 1 (2,71, 7,20 et 11,33 g/cm3), ce qui est proche des valeurs calculées à l’aide des pesées. Les objets en aluminium et en plomb sont facilement reconnaissables par leur masse volumique.

Pour l’objet en fonte, la masse volumique seule ne suffit pas à écarter d’autres métaux, comme le zinc (masse volumique connue de 7,13 g/cm3 répertoriée dans le tableau 1). Quand la masse volumique d’un objet approche celle de plusieurs métaux et alliages (par exemple, le zinc, le fer et l’étain), d’autres propriétés telles que le magnétisme et la couleur sont nécessaires pour identifier le matériau.

Masse volumique connue de métaux et d’alliages sélectionnés

Le tableau 1 donne la masse volumique connue de métaux et d’alliages sélectionnés par ordre croissant (ASTM, 2006; Lide, 1998).

Tableau 1 : Masse volumique connue de métaux et d’alliages sélectionnés
Métal ou alliage Masse volumique (g/cm3)
Aluminium 2,71
Alliages d’aluminium 2,66–2,84
Zinc 7,13
Fonte (grise) 7,20
Étain 7,30
Acier (non allié) 7,86
Acier inoxydable 7,65–8,03
Laiton (à cartouche : 70 % de cuivre, 30 % de zinc) 8,52
Laiton (rouge : 85 % de cuivre, 15 % de zinc) 8,75
Maillechort (65 % de cuivre, 18 % de nickel, 17 % de zinc) 8,75
Bronze (85 % de cuivre, 5 % d’étain, 5 % de zinc, 5 % de plomb) 8,80
Nickel 8,89
Cuivre 8,94
Argent 10,49
Plomb 11,33
Or 19,30

Détails concernant la balance

Une balance à dispositif de pesée sous le socle est généralement munie d’une plaque d’ouverture qui cache le crochet interne. La figure 2 illustre l’emplacement de la plaque sous le socle de la balance.

Dessous du socle de la balance. La plaque d’ouverture est encadrée en rouge.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0359
Figure 2. Balance à dispositif de pesée sous le socle.

La figure 3 montre le détail de la plaque fermée; à la figure 4, la plaque a été ouverte par rotation pour laisser voir le crochet à l’intérieur.

Vue rapprochée du dessous du socle de la balance montrant la plaque métallique qui cache le crochet intérieur.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0360
Figure 3. Vue rapprochée du dessous du socle de la balance montrant la plaque métallique amovible qui cache le crochet intérieur.

Vue rapprochée du dessous du socle de la balance montrant le crochet intérieur, une fois la plaque métallique ouverte par rotation.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0361
Figure 4. Vue rapprochée du dessous du socle de la balance montrant le crochet intérieur, une fois la plaque métallique ouverte par rotation.

La figure 5 montre un fil métallique recourbé aux deux extrémités de façon à former des crochets. La figure 6 montre le crochet à une extrémité du fil métallique fixé au crochet intérieur dans le socle de la balance.

Fil métallique aux deux extrémités recourbées de façon à former des crochets.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0363
Figure 5. Fil métallique aux deux extrémités recourbées de façon à former des crochets.

Détail du fil métallique recourbé aux deux extrémités de façon à former des crochets. Le crochet supérieur est fixé au crochet intérieur de la balance.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0362
Figure 6. Vue rapprochée du fil métallique recourbé aux deux extrémités de façon à former des crochets. Le crochet supérieur est fixé au crochet intérieur de la balance.

La figure 7 montre la balance en train d’être posée sur un support en Plexiglas où un trou a été percé sur le dessus. Le trou donne accès au crochet sous le socle de la balance.

La balance en train d’être posée sur un support en Plexiglas et le crochet sur le point de franchir le trou percé dans le support.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0365
Figure 7. La balance en train d’être posée sur un support en Plexiglas et le crochet sur le point de franchir le trou percé dans le support.

La figure 8 montre la balance posée sur le support en Plexiglas et le coupon rectangulaire en cuivre pur en train d’être pesé dans l’air. La figure 9 montre la balance posée sur le support en Plexiglas et le coupon rectangulaire en cuivre pur en train d’être pesé dans l’eau. Un plus petit support en Plexiglas maintient le bécher à la bonne hauteur.

Coupon rectangulaire en cuivre pur en train d’être pesé dans l’air.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0366
Figure 8. Coupon rectangulaire en cuivre pur en train d’être pesé dans l’air.

Coupon rectangulaire en cuivre pur immergé dans l’eau.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0367
Figure 9. Coupon rectangulaire en cuivre pur immergé dans l’eau.

La figure 10 donne un exemple d’objet doté d’une ouverture où des bulles d’air se sont logées. Il faut s’assurer qu’aucune bulle d’air n’est emprisonnée dans l’objet. Autrement, la pesée serait inexacte.

Trois bulles d’air sont visibles dans l’ouverture.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0375
Figure 10. Trois bulles d’air logées dans une ouverture.

Renseignements supplémentaires

Utilisation d’un solvant autre que l’eau

S’il ne convient pas d’immerger un objet dans l’eau, comme un objet en fer, sensible à la rouille, on utilisera un solvant organique, comme l’acétone ou l’éthanol anhydre. Il faut alors disposer d’un système de ventilation convenable et de l’équipement de protection individuelle approprié. Se reporter à la fiche signalétique du solvant utilisé pour connaître l’équipement recommandé. À 20 °C, la masse volumique de l’acétone est de 0,790 g/cm3 et celle de l’éthanol anhydre, de 0,789 g/cm3. S’il y a lieu d’utiliser l’un de ces liquides, il faudra peut-être mesurer la masse volumique d’un objet dans l’eau, puis dans l’autre liquide, et comparer ensuite les résultats.

Conseils pour l’adaptation d’une balance

Autre support pour la balance

En l’absence d’un support, on peut utiliser une feuille de contreplaqué percée qu’on fixera au rebord d’un comptoir à l’aide de serre-joints (figure 11).

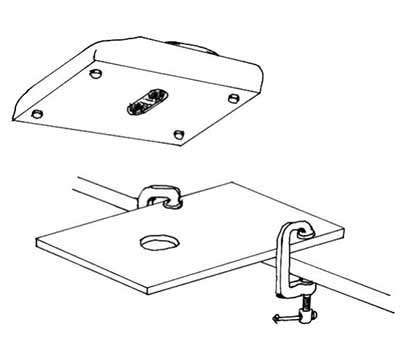
Croquis d’une feuille de contreplaqué fixé au rebord d’un comptoir et d’une balance sur le point d’y être posée.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0296
Figure 11. Un support de balance composé de contreplaqué et de serre-joints.

Balance sans dispositif de pesée sous le socle

Pour déterminer la masse volumique d’un objet, il est possible d’utiliser une balance sans dispositif de pesée sous le socle, mais il faut alors fabriquer un cadre auquel suspendre l’objet sous la balance et en transférer le poids à cette dernière. La balance sera fixée sur une plateforme. La figure 11 donne un exemple de montage possible. (Dans le cas qui nous occupe, le trou percé, que l’on peut voir à la figure 11, n’est pas nécessaire.) Un cadre à quatre côtés (semblable à un encadrement de tableau) entoure la balance et sa plateforme et ne repose que sur le plateau sans toucher à quelque autre pièce de la balance (figure 12). La balance est tarée (mise à zéro) avec le cadre et le crochet en place. L’objet est ensuite suspendu au crochet du cadre et pesé dans l’air, puis dans le liquide, comme dans les étapes 4 à 9 expliquées précédemment dans la section Procédure : comment déterminer la masse volumique d’un objet en métal.

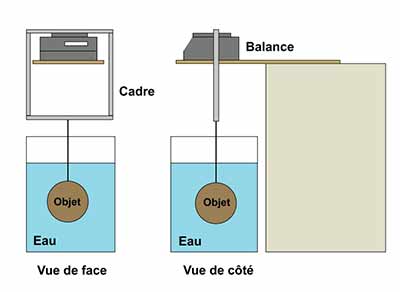
Croquis du cadre reposant sur le plateau de la balance, montré sous deux angles.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0428
Figure 12. Vue de face (à gauche) et vue de côté (à droite) d’une balance sans dispositif de pesée sous le socle. Le haut du cadre rectangulaire repose sur le plateau de la balance, et l’objet est suspendu au bas du cadre.

Aspects scientifiques du calcul de la masse volumique

Flottabilité et principe d’Archimède

Les techniques sur lesquelles repose cette méthode datent du troisième siècle avant Jésus-Christ. Dans son ouvrage Traité des corps flottants, Archimède de Syracuse avance que, si un objet est immergé dans un liquide et pesé, son poids sera inférieur à son poids réel en raison du poids du liquide déplacé. L’histoire raconte qu’Archimède a appliqué cette idée à une couronne pour démontrer qu’elle n’était pas faite d’or pur, mais bien d’un alliage d’or et d’argent (Heath, 1920).

Si l’objet semble plus léger dans le liquide, c’est qu’une force verticale pousse l’objet : c’est la poussée hydrostatique, mieux connue sous le nom « poussée d’Archimède ». Comme la pression du liquide augmente avec la profondeur, la pression est plus forte sur la partie inférieure de l’objet (elle pousse l’objet vers le haut) que sur sa partie supérieure (elle le pousse vers le bas). La différence entre la poussée vers le haut et la poussée vers le bas produit la poussée d’Archimède. La poussée d’Archimède, poussant l’objet vers le haut, s’oppose à la gravité, qui l’attire vers le bas. Si la poussée d’Archimède est moins forte que la gravité, l’objet coulera, mais il semblera moins lourd dans le liquide que dans l’air. Si la poussée d’Archimède est plus forte que la gravité, l’objet flottera à la surface du liquide.

La masse volumique d’un objet se calcule à l’aide de la formule susmentionnée, soit :


Une fois connue, la masse volumique peut servir à calculer le volume de l’objet grâce à la formule suivante :

Volume de l’objet = (masse dans l’air)/(masse volumique de l’objet)

Comme l’eau, l’air produit aussi une poussée d’Archimède. (C’est pourquoi les ballons gonflés à l’hélium s’élèvent.) Dans la présente méthode, la poussée d’Archimède dans l’air est trop faible pour avoir une incidence, mais il faut en tenir compte lorsqu’une pesée de haute précision est nécessaire (Skoog et al., 2014).

Détermination de la masse volumique par le volume déplacé

Un moyen plus simple, mais moins précis, de déterminer la masse volumique est de placer l’objet dans un liquide et de mesurer le volume de liquide déplacé. Cette méthode est utilisable pour de petits objets qui tiennent dans un cylindre gradué pour, par exemple, déterminer si l’objet est fait de plomb ou d’un métal moins dense.

Voici comment procéder. Trouver un cylindre gradué d’un diamètre un peu plus grand que l’objet. Déterminer la masse de l’objet avec une balance appropriée. Mettre de l’eau dans le cylindre gradué et noter le niveau atteint. Immerger complètement l’objet dans l’eau en prenant soin d’éviter la formation de bulles d’air, puis noter encore le niveau de l’eau. Le volume de l’objet est égal à la différence entre le volume final et le volume initial lus sur le cylindre gradué, et la masse volumique à la masse divisée par le volume de l’objet.

Par exemple, on a pesé une figurine d’orignal. Sa masse est de 4,088 g. La figure 13 montre la figurine hors du cylindre gradué et la figure 14, la figurine immergée. Dans le cylindre gradué, l’eau est passée de 5,0 mL à 5,6 mL quand la figurine a été immergée; le volume a donc augmenté de 0,6 mL. Sauf erreur de mesure du volume, la masse volumique calculée est de 4,088 g/0,6 mL = 6,8 g/cm3. (Note : 1 mL = 1 cm3.) C’est inférieur à la masse volumique du zinc; on peut en déduire qu’il s’agit d’un alliage de zinc et d’un métal plus léger, peut-être bien du magnésium ou de l’aluminium. Mais étant donné le faible volume, la mesure laisse place à l’incertitude. Vu le cylindre gradué utilisé, le volume ne peut se mesurer qu’à 0,1 mL près, si bien qu’il pourrait se situer entre environ 0,5 mL et 0,7 mL. Par conséquent, la masse volumique pourrait se trouver quelque part entre 4,088 g/0,7 mL = 5,8 g/cm3 et 4,088 g/0,5 mL = 8,2 g/cm3. Dans cette fourchette de mesures, la figurine pourrait être faite de zinc, de fer, d’étain, d’acier ou d’autres alliages, mais il est impossible qu’elle se compose d’aluminium pur ou de plomb pur. En fait, l’analyse a montré qu’elle est faite d’étain, d’une masse volumique de 7,30 g/cm3.

Le niveau de l’eau se trouve juste au-dessus de la ligne marquant les 5 mL.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0373
Figure 13. Un petit objet en métal avant son immersion dans l’eau contenue dans un cylindre gradué de 25 mL. Noter le niveau de l’eau.

Un petit objet en métal après son immersion dans l’eau contenue dans un cylindre gradué de 25 mL. Le niveau d’eau est d’environ 0,6 mL plus haut qu’avant l’immersion de l’objet.

© Gouvernement du Canada, Institut canadien de conservation. ICC 120260-0374
Figure 14. Un petit objet en métal après son immersion dans l’eau contenue dans un cylindre gradué de 25 mL. Le niveau d’eau est d’environ 0,6 mL plus haut qu’avant l’immersion de l’objet.

Autres utilisations

Les méthodes susmentionnées sont utiles à d’autres fins que la seule identification des métaux par leur masse volumique.

Masse des métaux de fonderie

Pour couler une sculpture, il faut connaître la quantité de métal requise afin de remplir le moule d’un modèle. S’il est possible d’immerger le modèle à couler, on peut en déterminer le volume par les techniques susmentionnées. On calculera ensuite la masse m du métal à partir du volume V du modèle et la masse volumique ρ du métal par la formule m = ρV. (Rappel : le travail exige habituellement du métal supplémentaire pour remplir les canaux qui guident le métal fondu dans le moule.)

Remerciements

Merci à Meaghan Walley, à Lucy ‘t Hart et à Catherine Machado, anciennes stagiaires à l’ICC, d’avoir contribué à l’élaboration de la présente Note.

Références

ASTM G1-03. « Standard Practice for Preparing, Cleaning, and Evaluating Corrosion Test Specimens », dans Annual Book of ASTM Standards, vol. 03.02, West Conshohocken (Pennsylvanie), American Society for Testing and Materials, 2006, p. 17-25.

Heath, T.L. Archimedes (en anglais seulement), New York (New York), MacMillan, 1920.

Lide, D. R. (directeur de publication). CRC Handbook of Chemistry and Physics, 79th ed., Boca Raton (Floride), CRC Press, 1998, p. 12-191 et 12-192.

Skoog, D. A., D. M. West, F. J. Holler et S. R. Crouch. Fundamentals of Analytical Chemistry, 9e éd., Belmont (Californie), Brooks/Cole, 2014, p. 22-23.

Rédigé par Lyndsie Selwyn
Révisé en 2023

Première date de publication : 2016

Also available in English.

© Gouvernement du Canada, Institut canadien de conservation, 2023

ISSN 1928-1455

Détails de la page

Date de modification :