Utilisant des algorithmes d’apprentissage automatique pour prévoir la surveillance des maladies en Ontario

 Téléchargez cet article en format PDF
Téléchargez cet article en format PDFPublié par : L’Agence de la santé publique du Canada
Numéro : Volume 46–6 : Intelligence artificielle en santé publique
Date de publication : 4 juin 2020
ISSN : 1719-3109
Soumettre un article
À propos du RMTC
Naviguer
Volume 46–6, le 4 juin 2020 : Intelligence artificielle en santé publique
Science de la mise en œuvre
Bon temps mauvais temps : Prévision automatisée de la cryptosporidiose saisonnière en Ontario à base d’apprentissage machine
Olaf Berke1, Lise Trotz-Williams1,2, Simon de Montigny3,4
Affiliations
1 Department of Population Medicine, Collège de médecine vétérinaire de l’Ontario, Université de Guelph, Guelph, ON
2 Wellington-Dufferin Guelph Public Health, Guelph, ON
3 École de santé publique - Département de médecine sociale et préventive, Université de Montréal, Montréal, QC
4 Centre de recherche du CHU Sainte-Justine, Montréal, QC
Correspondance
Citation proposée
Berke O, Trotz-Williams L, de Montigny S. Bon temps mauvais temps : Prévision automatisée de la cryptosporidiose saisonnière en Ontario grâce à l’apprentissage machine. Relevé des maladies transmissibles au Canada 2020;46(6):218–24. https://doi.org/10.14745/ccdr.v46i06a07f
Mots-clés : surveillance des maladies, apprentissage automatique, apprentissage statistique, cryptosporidiose, réseau neuronal artificiel, SARIMA, prévisions, séries chronologiques saisonnières
Résumé
Contexte : L’augmentation de l’utilisation des mégadonnées et de la modélisation prédictive connexe fondée sur des algorithmes d’apprentissage automatique au cours des deux dernières décennies a fourni de nouvelles possibilités de surveillance des maladies et de préparation de la santé publique. Les mégadonnées s’accompagnent de la promesse d’une production et d’un accès plus rapide à des renseignements précis, ce qui pourrait faciliter la précision prédictive en santé publique (« santé publique de précision »). À titre d’exemple, nous avons envisagé de prévoir l’évolution future de l’incidence mensuelle de la cryptosporidiose en Ontario.
Méthodologie : L’approche statistique traditionnelle en matière de prévision est le modèle de moyenne mobile intégrée saisonnière autorégressive (SARIMA). Nous avons appliqué le modèle SARIMA et une approche de réseau de neurones artificiels (RNA), plus précisément un réseau de neurones à propagation avant, pour prévoir l’incidence mensuelle de la cryptosporidiose en Ontario en 2017 en utilisant les données de 2005 à 2016 comme ensemble d’apprentissage initial. Les deux approches de prévision sont automatisées pour les rendre pertinentes au contexte de la surveillance des maladies. Nous avons comparé les prévisions résultantes en utilisant la racine de l’erreur quadratique moyenne (REQM) et l’erreur absolue moyenne (EAM) comme mesures de la précision des prévisions.
Résultats : La cryptosporidiose est une maladie saisonnière qui atteint son apogée en Ontario à la fin de l’été. Dans cette étude, le modèle SARIMA et les approches de prévision du RNA ont saisi le schéma saisonnier de la cryptosporidiose. Contrairement à des études semblables publiées dans la documentation scientifique, les prévisions du RNA sur la cryptosporidiose étaient légèrement moins précises que les prévisions du modèle SARIMA.
Conclusion : Les approches du RNA et du SARIMA conviennent à la prévision automatisée des données des séries chronologiques en santé publique provenant des systèmes de surveillance. Les études futures devraient utiliser des algorithmes supplémentaires (e.g. forêts d’arbres décisionnels) et évaluer l’exactitude en utilisant d’autres maladies comme études de cas et en réalisant des études de simulation rigoureuses. La différence entre les prévisions de l’algorithme d’apprentissage automatique, c.-à-d. le RNA, et le modèle d’apprentissage statistique, c.-à-d. le SARIMA, doit être prise en compte en ce qui concerne les différences philosophiques entre les deux approches.
Introduction
La cryptosporidiose est une maladie diarrhéique potentiellement mortelle qui touche les humains et les animaux. Elle est causée par le parasite protozoaire Cryptosporidium sp.Note de bas de page 1. Une vingtaine des 26 espèces connues ont été associées à des infections humainesNote de bas de page 2. La majorité des infections humaines sont causées par le C. hominis et le C. parvum, qui sont principalement liées respectivement à des transmissions anthropiques et zoonotiquesNote de bas de page 3. La principale voie d’infection pour les humains est la consommation (notamment pendant la baignade) d’eau contaminée par les oocystes des parasites.
La cryptosporidiose est souvent asymptomatique, mais elle peut entraîner des maladies gastro-intestinales légères à graves, voire le décès. La prévalence des infections chez les humains en Amérique du Nord varie entre 1 % et 4 % par année, mais peut atteindre 20 % ailleursNote de bas de page 4. Bien que la cryptosporidiose soit probablement sous-déclarée, on sait qu’elle est plus fréquente chez les enfants et les personnes immunodéprimées. Aucun traitement prophylactique n’est disponible, ce qui fait de la préparation de la santé publique fondée sur la surveillance une option préventive importante.
De nouvelles possibilités d’application des statistiques, de l’épidémiologie et de la surveillance des maladies en santé publique sont apparues au cours des deux dernières décennies depuis l’avènement des mégadonnéesNote de bas de page 5Note de bas de page 6. Gunther Eysenbach a introduit le terme « infodémiologie » pour l’utilisation des mégadonnées (plus précisément des données sur l’utilisation et le comportement dans les médias sociaux) dans la surveillance de la santéNote de bas de page 7. Un exemple frappant d’infodémiologie est le projet Google Flu Trends, qui a prédit des éclosions régionales de grippe de 7 à 10 jours avant les méthodes de surveillance conventionnelles du Center for Disease Control and Prevention (CDC), mais qui a largement surestimé la prévalence de la grippeNote de bas de page 8. Ce projet est un exemple manifeste des possibilités ainsi que des risques liés aux mégadonnées, qu’on appelle « l’orgueil des mégadonnées »Note de bas de page 8Note de bas de page 9.
Les mégadonnées sont souvent caractérisées par les cinq V : volume, variété, vitesse, véracité et valeurNote de bas de page 9. L’orgueil de mégadonnées fait référence à la véracité des données. La promesse des mégadonnées est que de grandes quantités de données (volume) de différents types et de sources différentes (variété) fournissent une représentation plus complète et précise de la réalité, ce qui mène à la « santé publique de précision »Note de bas de page 10. Toutefois, lorsque les données ne sont pas représentatives de la population d’intérêt, les inférences prédictives sont biaisées.
La surveillance des maladies donne lieu à une situation de mégadonnées en raison de la vitesse et du volume des données : les données sont constamment mises à jour et leur taille augmente. La nature dynamique des données de surveillance des maladies exige une approche automatisée de l’analyse et de la prévision. La méthode traditionnelle de modélisation statistique en série chronologique est le modèle de moyenne mobile intégrée saisonnière autorégressive (SARIMA) proposé par Box et JenkinsNote de bas de page 11. Un algorithme d’apprentissage automatique largement utilisé pour la prévision des séries chronologiques est le réseau neuronal artificiel (RNA) (à propagation avant)Note de bas de page 12. Nous avons appliqué ces deux approches de prévision pour prévoir l’incidence mensuelle de la cryptosporidiose en Ontario en 2017 en utilisant les données de 2005 à 2016 comme ensemble initial d’apprentissage. Nous avons comparé ces approches de prévision en utilisant l’incidence de 2017 comme données de test, avec la racine de l’erreur quadratique moyenne (REQM) et l’erreur absolue moyenne (EAM) de prévision comme mesures de précision.
Des comparaisons semblables ont été rapportées dans la documentation scientifique. Zhang et QiNote de bas de page 13 ont comparé le SARIMA et le RNA à l’aide de simulations et ont montré que le RNA offre toujours de meilleures prévisions que le SARIMA, lorsque les données sont prétraitées de façon appropriée. Kane et coll.Note de bas de page 14 ont comparé les prévisions de foyers de grippe aviaire H5N1 avec le SARIMA à celles de l’algorithme de forêts d’arbres décisionnels et ont conclu que l’apprentissage automatique offre une meilleure capacité de prédiction par rapport à la modélisation des séries chronologiques. De même, dans une étude sur l’incidence de la fièvre typhoïde en Chine, Zhang et coll. ont comparé la modélisation SARIMA à trois architectures différentes de RNA; les chercheurs ont conclu que les trois algorithmes de réseau neuronal surclassent le modèle statistiqueNote de bas de page 15.
Cette étude vise à comparer les deux approches utilisées pour automatiser la prévision des taux d’incidence mensuels de la cryptosporidiose en Ontario pour l’année 2017. Les objectifs spécifiques étaientNote de bas de page 1 de comparer la précision des prévisions en utilisant la REQM;Note de bas de page 2 de comparer les prévisions en utilisant l’EAM; etNote de bas de page 3 de comparer visuellement les taux d’incidence prévus aux séries chronologiques observées.
Méthodes
Les données que nous avons utilisées étaient des dénombrements mensuels d’incidence de la cryptosporidiose en Ontario pour les années 2005 à 2017 tels que déclarés à Santé publique Ontario et disponibles à partir des pages d’accueil respectivesNote de bas de page 16. À des fins d’analyse, nous divisons l’ensemble de données en données d’apprentissage (incidences mensuelles de 2005 à 2016) et en données de test (incidences mensuelles de 2017).
À des fins d’exploration, nous avons signalé des fourchettes d’incidence moyenne annuelle et mensuelle dans les données d’apprentissage et nous avons inspecté les données avec la décomposition saisonnière et tendancielle en utilisant la méthode de Loess (STL)Note de bas de page 17. La composante saisonnière a été présumée invariante dans le temps ou périodique, tandis que la composante de tendance a été trouvée en utilisant une fenêtre mobile de 73 mois, ou six ans plus un mois.
Le SARIMANote de bas de page 11 est un modèle de génération de données qui comprend des composantes saisonnières et des tendances. Il est utilisé pour décrire les autocorrélations dans une série chronologique et pour prédire les valeurs futures. Il est décrit par l’ordre des filtres appliqués pour supprimer les composantes saisonnières et de tendance ainsi que par l’ordre des corrélations décalées dans la série filtrée. La série filtrée est supposée être une fonction stationnaire et gaussienne. On résume le SARIMA comme suit : SARIMA (p,d,q)(P,D,Q) S, où S désigne la durée de la saison (ici 12 mois), d et D désignent les filtres de différence non saisonnière et saisonnière pour éliminer les composantes tendancielles et saisonnières, respectivement. De plus, p et P sont des ordres des paramètres d’autocorrélation non saisonniers et saisonniers, respectivement. Enfin, q et Q désignent l’ordre non saisonnier et saisonnier des paramètres de moyenne mobile. L’approche de modélisation SARIMA a été automatisée en utilisant l’estimation du maximum de vraisemblance et la sélection progressive rétrospective du modèle avec le critère d’information bayésienne (BIC). Le SARIMA, adapté aux données d’apprentissage 2005 à 2016, a ensuite été utilisé pour prévoir les incidences mensuelles pour les données de test de 2017.
Le RNA est un algorithme automatisé et axé sur les données qui permet de prévoir les données des séries chronologiques. Bien qu’une variété d’architectures de RNA existeNote de bas de page 18Note de bas de page 19, nous avons appliqué le réseau neuronal multicouche de base, à propagation avant, avec une seule couche cachée dans cette étudeNote de bas de page 12. Plus précisément, le RNA est décrit comme RNA (p,P,k) S, où p, P et S ont les mêmes significations que dans le modèle SARIMA, et k indique le nombre de nœuds dans la couche cachée. La sélection automatique des valeurs d’ordre du RNA était la suivante : S=12 est connu; k était la valeur arrondie de (p+P+1)/2, où P était réglé à P=1 pour tenir compte de la saisonnalité linéaire; et p a été sélectionné comme l’ordre optimal d’un modèle autorégressif convenant au reste du terme de la série décomposée de la STL.
Nous avons appliqué l’algorithme du RNA comme suit : les combinaisons linéaires de données d’entrée ont été soumises à la fonction d’activation sigmoïde non linéaire 1/(1+exp[– z]) comme sortie d’une couche cachée, et les résultats de la couche cachée ont ensuite été agrégés sous forme de combinaisons linéaires, ce qui a donné lieu à la sortie finale. Le RNA a été formé en utilisant 100 répétitions, c’est à dire 100 valeurs de départ aléatoires différentes pour les paramètres de poids des combinaisons linéaires entre les couches d’entrée et cachées, ainsi que les couches cachées et de sortie. De plus, la série d’entrées (c.-à-d. les données de 2005 à 2016) a été prétraitée au moyen d’une sélection automatique du paramètre de transformation de Box–Cox (par la méthode GuerreroNote de bas de page 12) suivie d’une studentisation (c.-à-d. le centrage et la mise à l’échelle). Pour chaque répétition, l’algorithme a été entraîné par un processus expérimental itératif d’optimisation d’une fonction de perte. L’ensemble des prévisions qui en a résulté a été moyennée sur toutes les itérations.
Les deux approches de prévision fournissent des intervalles de prévision. L’intervalle de prévision du SARIMA était fondé sur l’estimation du paramètre du modèle. L’intervalle de prévision du RNA était fondé sur 1 000 exemplaires de chemins générés par bootstrapNote de bas de page 12, c’est à dire en utilisant des résidus passés rééchantillonnés. De plus, les deux approches de prévision ont été comparées par leurs mesures d’exactitude (REQM et EAM) pour les prévisions mensuelles et les données d’essai observées de l’année 2017.
Toutes les analyses de données ont été effectuées dans RNote de bas de page 20 et RStudioNote de bas de page 21 à l’aide de la librairie « forecast »Note de bas de page 12.
Résultats
La série chronologique des incidences de cryptosporidiose signalées mensuellement en Ontario pour les années 2005 à 2016 est dominée par une composante saisonnière, avec des pics en été et seulement une faible – voire aucune – tendance à la hausse (figure 1). La décomposition du STL à la figure 2 confirme cette impression. La série chronologique des données sur la formation est relativement courte, 12 ans comprenant 4 152 cas, soit une moyenne annuelle de 346 cas, ce qui équivaut à environ 2,57 cas annuels pour 100 000 personnes à risque. Le nombre moyen de cas mensuels était de 29, allant de 6 à 109 cas de 2005 à 2016.
Figure 1 : Graphique chronologique de l’incidence mensuelle de la cryptosporidiose en Ontario de 2005 à 2016
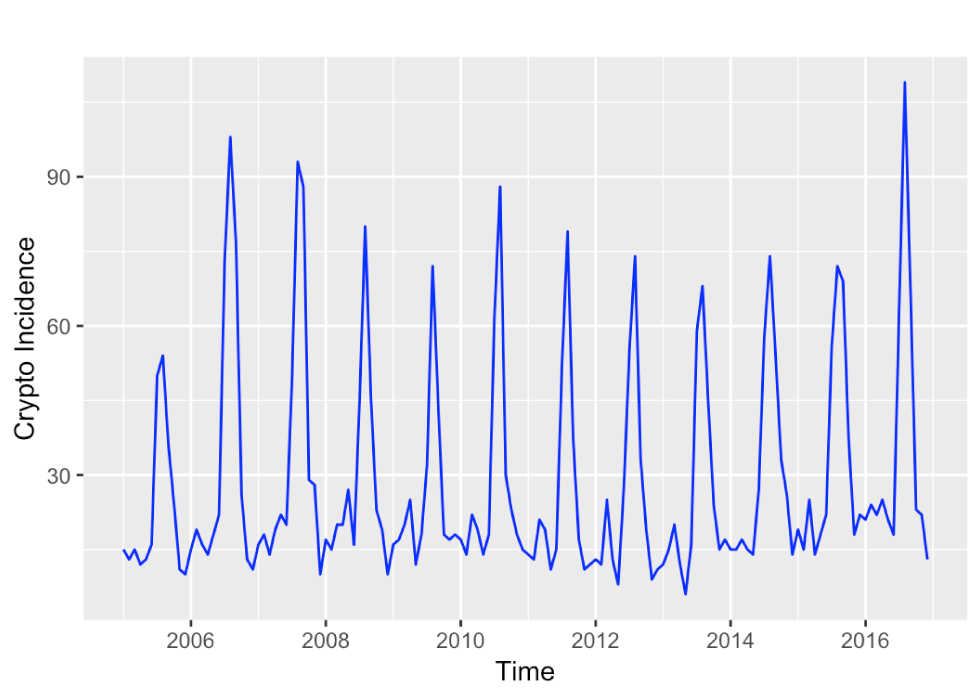
Description textuelle : Figure 1
Figure 1 : Graphique chronologique de l’incidence mensuelle de la cryptosporidiose en Ontario de 2005 à 2016
Graphique chronologique de l’incidence mensuelle de la cryptosporidiose en Ontario de 2005 à 2016. L’incidence varie d’environ 10 à 20 cas par mois sans tendance temporelle évidente, mais une forte augmentation saisonnière à environ 70 à 90 cas par mois.
Figure 2 : Série chronologique des incidences mensuelles de la cryptosporidiose de 2005 à 2016Figure 2 note a
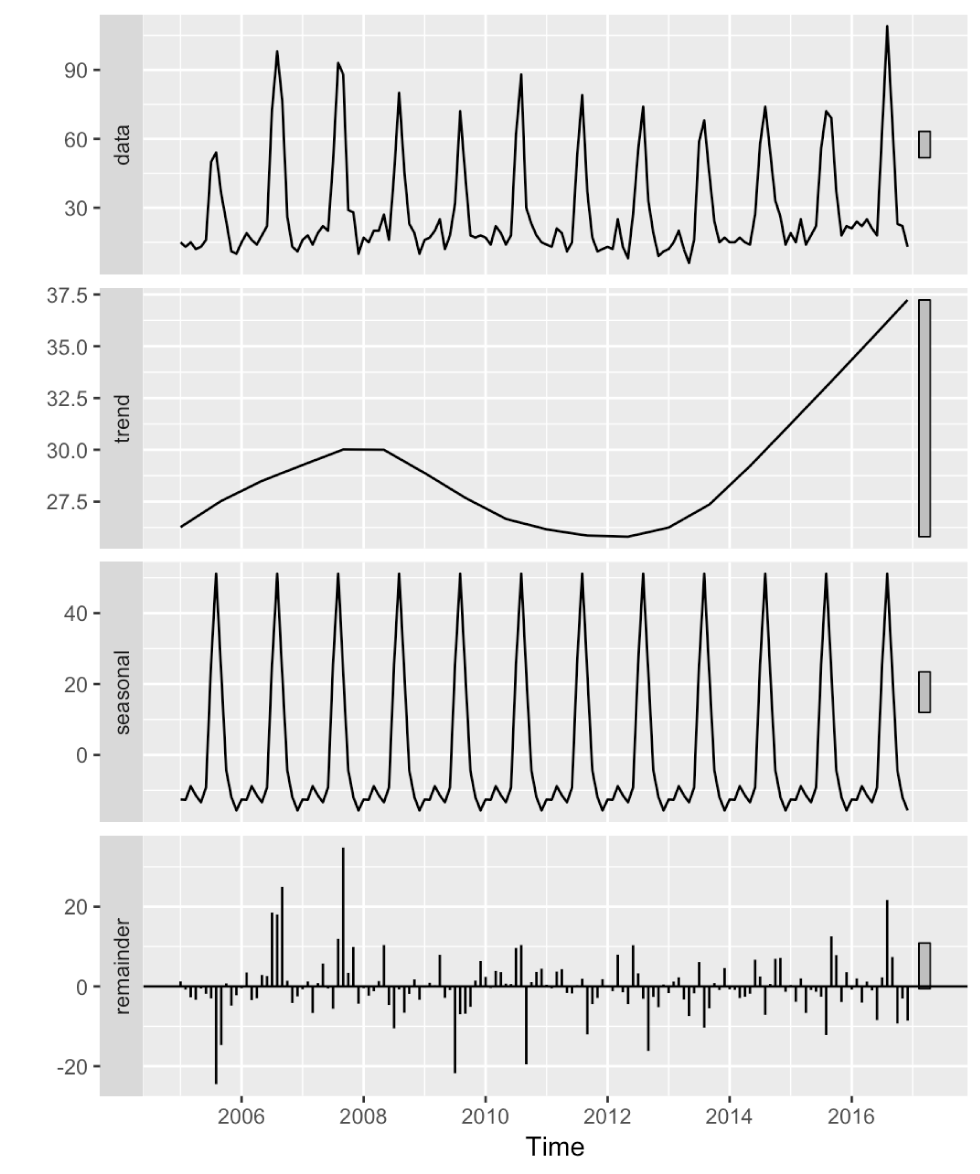
Description textuelle : Figure 2
Figure 2 : Série chronologique des incidences mensuelles de la cryptosporidiose de 2005 à 2016Figure 2 note a
Série chronologique des incidences mensuelles de la cryptosporidiose de 2005 à 2016. Cette figure présente la série chronologique ainsi que la décomposition saisonnière et tendancielle au moyen de la méthode Loess (STL). La figure combine quatre graphiques de la série chronologique disposés en rangées de sorte que les axes temporels sont alignés aux fins de comparaison. Le graphique supérieur présente la série chronologique observée de cas de cryptosporidiose. Ensuite, on trouve des graphiques pour les composantes tendancielles, saisonnières et restantes résultant de la décomposition de la STL.
La composante de la tendance est relativement stable, se situant principalement entre 25 et 30 cas par mois, avec une légère augmentation au cours des quatre dernières années à environ 35 cas par mois.
La composante saisonnière est la caractéristique principale et représente la plus grande proportion de la variabilité de la série chronologique. La tendance saisonnière est dominée par une forte augmentation du nombre de cas à la fin de l’été, lorsque le nombre de cas passe d’un niveau d’environ -10 à environ +50 cas par mois.
Le reste de la composante varie approximativement entre -20 et +20 cas par mois. Elle ne présente aucune tendance évidente; la variation semble aléatoire.
La sélection automatisée par étapes du modèle a abouti à un SARIMA (1,0,0)(1,1,0)12 dont les estimations des paramètres du modèle sont le paramètre autorégressif du premier ordre AR (1)=0,41 (erreur standard [SE]=0,08) et le paramètre autorégressif saisonnier du premier ordre SAR (1)=0,35 (SE=0,10) (figure 3).
Figure 3 : Prévisions des incidences mensuelles de cryptosporidiose de 2017 avec des intervalles de prévision de 80 % et 95 % à partir d’un SARIMA (1,0,0) (1,1,0)12
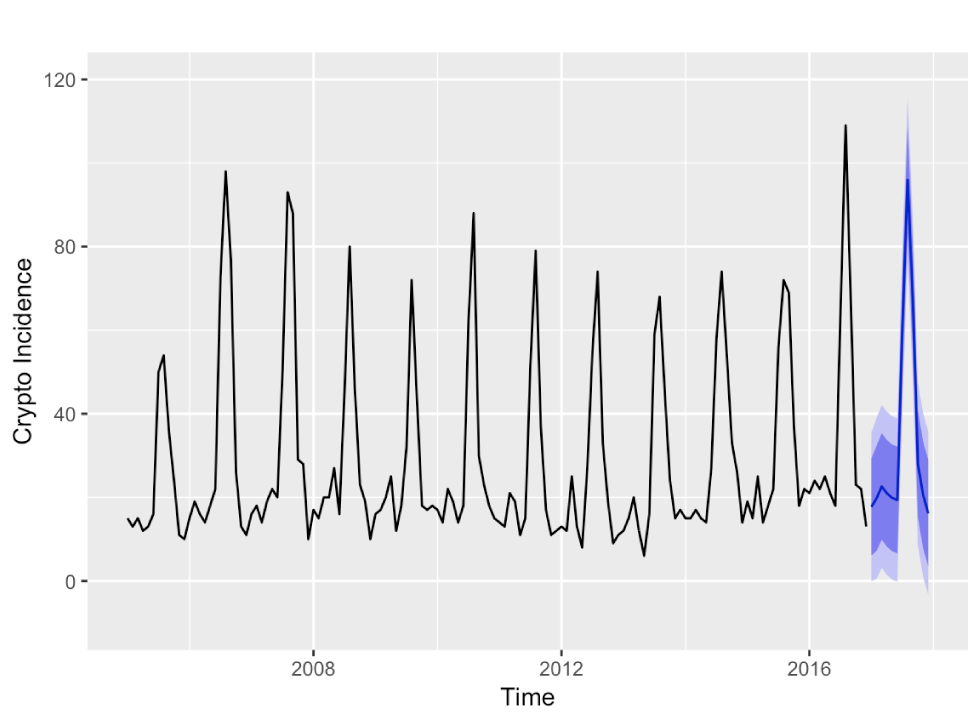
Description textuelle : Figure 3
Figure 3 : Prévisions des incidences mensuelles de cryptosporidiose de 2017 avec des intervalles de prévision de 80 % et 95 % à partir d’un SARIMA (1,0,0) (1,1,0)12
Prévisions des incidences mensuelles de cryptosporidiose de 2017 avec des intervalles de prévision de 80 % et 95 % à partir d’un modèle SARIMA (1,0,0) (1,1,0)12. Les prévisions de 2017 rendent bien compte de la tendance saisonnière. L’intervalle de prévision de 95 % est large et atteint le négatif pour le dernier mois, c’est-à-dire décembre 2017.
Le RNA sélectionné automatiquement est d’ordre RNA (11,1,6)12, c.-à-d. que les 11 dernières observations plus la première observation saisonnière sont linéairement combinées en six nœuds d’une seule couche cachée. La série d’entrée a été transformée selon la méthode de Box-Cox avec un paramètre choisi automatiquement λ=0,21. Les prévisions du RNA sont visualisées avec des intervalles de prévision de 80 % et 95 % à la figure 4.
Figure 4 : Prévisions des incidences mensuelles de cryptosporidiose de 2017 avec des intervalles de prévision par bootstrap à 80 % et 95 % à partir d’un RNA (11,1,6)12
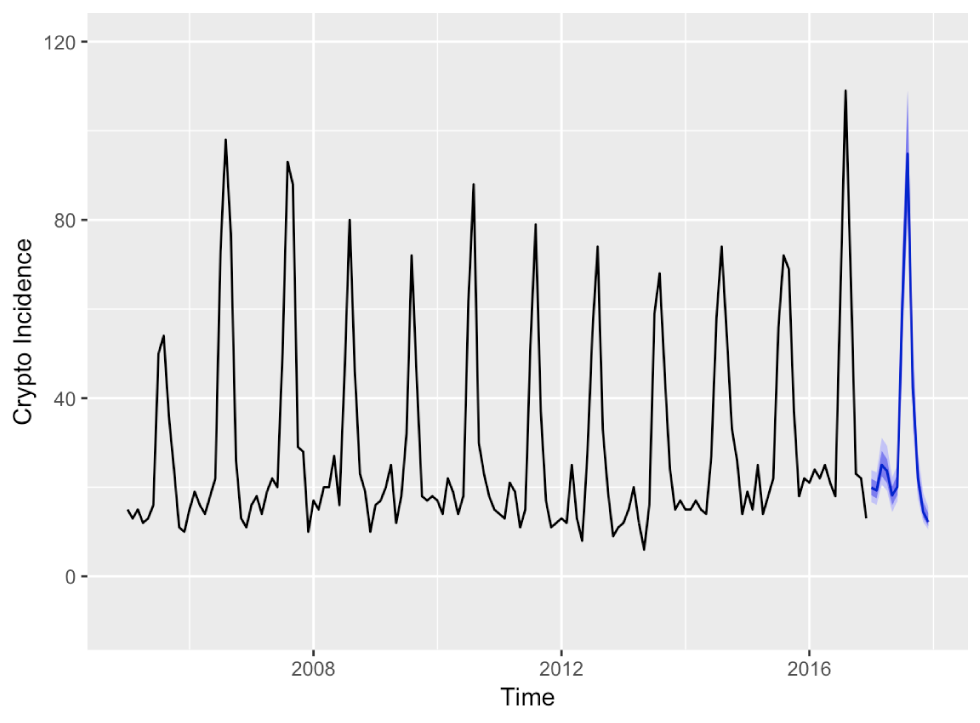
Description textuelle : Figure 4
Figure 4 : Prévisions des incidences mensuelles de cryptosporidiose de 2017 avec des intervalles de prévision par bootstrap à 80 % et 95 % à partir d’un RNA (11,1,6)12
Prévisions des incidences mensuelles de cryptosporidiose de 2017 avec des intervalles de prévision par bootstrap à 80 % et 95 % à partir d’un RNA (11,1,6)12. Les prévisions de 2017 rendent bien compte de la tendance saisonnière. L’intervalle de prévision est très étroit aux alentours de l’incidence prévue et il est toujours positif.
Les incidences mensuelles observées et les prévisions arrondies sont présentées au tableau 1 et à la figure 5 pour les deux modèles. Le tableau 2 présente les résumés du REQM et de l’EAM tirés des prévisions de 2017 pour les deux approches.
| Taux d’incidence par mois | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mois | janv. | févr. | mars | avril | mai | juin | juillet | août | sept. | oct. | nov. | déc. |
| Observé | 23 | 17 | 25 | 22 | 16 | 24 | 48 | 70 | 55 | 32 | 33 | 20 |
| SARIMA | 18 | 20 | 23 | 21 | 20 | 19 | 61 | 96 | 68 | 28 | 21 | 16 |
| RNA | 20 | 19 | 25 | 24 | 18 | 20 | 62 | 95 | 42 | 22 | 15 | 12 |
Figure 5: Graphique chronologique des incidences mensuelles de cryptosporidioses observées pour 2017 et des prévisions de l’approche SARIMA et du RNA
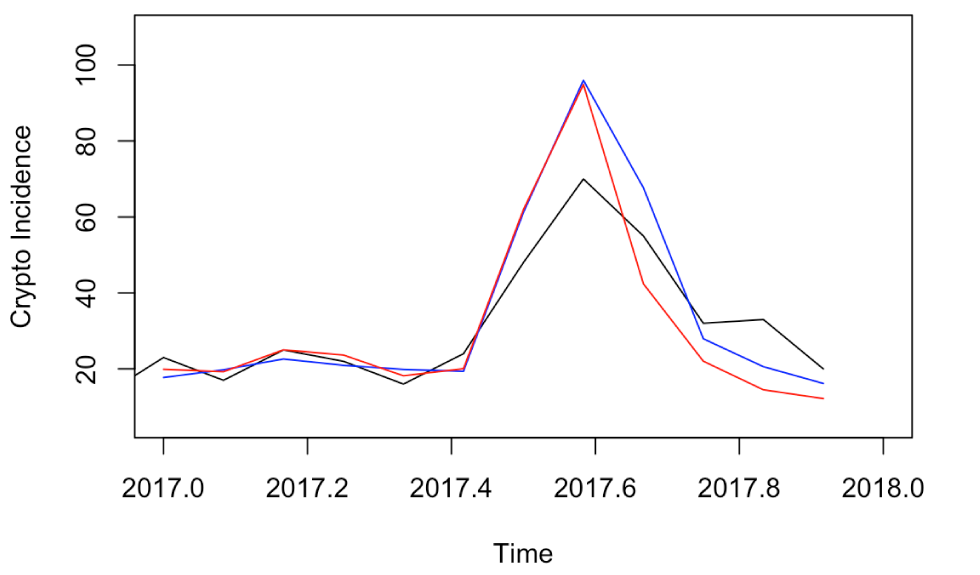
Description textuelle : Figure 5
Figure 5: Graphique chronologique des incidences mensuelles de cryptosporidioses observées pour 2017 et des prévisions de l’approche SARIMA et du RNA
Figure 5: Graphique chronologique des incidences mensuelles de cryptosporidioses observées pour 2017 et des prévisions de l’approche SARIMA et du RNA
Graphique chronologique des incidences mensuelles de cryptosporidioses observées pour 2017 et des prévisions de l’approche SARIMA et du RNA. Les prévisions pour les deux méthodes sont très précises pour les six premiers mois et surestiment le pic saisonnier d’août 2017. Compte tenu de l’augmentation de la période de prévision, les prévisions sont moins précises pour le reste de l’année.
| Modèle | REQM | EAM |
|---|---|---|
| SARIMA (1,0,0)(1,1,0)12 | 10,3 | 7,7 |
| RNA (11,1,6)12 | 11,2 | 8,4 |
Discussion
L’incidence mensuelle de la cryptosporidiose en Ontario est caractérisée par une tendance saisonnière dominante qui culmine généralement en août. Le court pic d’incidence peut appuyer le concept du comportement humain comme principal facteur d’infection puisque les conditions environnementales (e.g. la température ambiante) ne varient pas de la même façon que l’incidence. Aucune tendance à la hausse n’a été relevée, ce qui signifie que l’incidence n’est pas émergente.
Ni l’algorithme d’apprentissage automatique (c.-à-d. le RNA) ni la méthode d’apprentissage statistique (c.-à-d. le SARIMA) n’ont obtenu un rendement supérieur pour ce qui est de prédire l’incidence mensuelle de la cryptosporidiose. Alors que les prévisions du RNA étaient plus proches des observations pour six mois, le SARIMA a obtenu de meilleurs résultats pour un groupe différent de cinq mois; les deux méthodes étaient à égalité pour le mois de septembre 2017 (voir le tableau 1). Toutefois, les mesures de l’exactitude REQM et EAM indiquent un léger avantage pour les prévisions du SARIMA : la REQM du RNA et l’EAM étaient supérieurs de 0,9 et 0,7 unité, respectivement (voir le tableau 2).
Ce léger avantage pour le SARIMA est interprété comme suit : les prévisions du SARIMA sont, en moyenne, presque un cas par mois plus précises que les prévisions du RNA. Bien que ce résultat soit inattendu en ce qui concerne les rapports citésNote de bas de page 13Note de bas de page 14Note de bas de page 15, il est conforme à un examen systématiqueNote de bas de page 22 qui n’a trouvé aucune preuve de prédictions plus exactes des solutions de rechange à l’apprentissage machine à la modélisation de régression logistique statistique. Toutefois, il convient de noter qu’il s’agit d’une étude de cas et que les résultats sont propres à cet exemple. Bien que le SARIMA suppose des résidus de bruit blanc et une composante saisonnière additive, cela n’a pas été vérifié ici à l’aide de l’approche de modélisation automatisée. De même, le RNA est optimisé à l’aide de la rétropropagation, qui est connue pour avoir de la difficulté à trouver les estimations de paramètres optimalesNote de bas de page 19. Par conséquent, le RNA utilise les prévisions d’ensemble pour se prémunir contre les prévisions erronées individuelles.
Un prétraitement adéquat des données est important pour les algorithmes d’apprentissage automatiqueNote de bas de page 23. Cela signifie qu’une série chronologique doit être mise à l’échelle et centrée (c.-à-d. studentisée ou normalisée) avant l’analyse. Le prétraitement des données est une partie naturelle de l’approche de modélisation de la moyenne mobile intégrée autorégressive, car les effets saisonniers et les effets de tendance sont filtrés avant que le modèle ne soit adapté à la série chronologique. Dans notre étude, la sélection progressive du modèle a permis de filtrer un effet saisonnier, mais aucun effet de tendance n’a été identifié ou supprimé. Le RNA a été prétraité par une transformation Box-Cox, suivie d’un centrage et d’une mise à l’échelle.
L’analyse des mégadonnées est souvent présentée avec des algorithmes d’apprentissage automatique pour l’inférence, c.-à-d. la modélisation prédictive. Cela pourrait s’expliquer par l’impression que les méthodes statistiques traditionnelles ne conviennent pas aux défis des mégadonnées. Par exemple, la variété des données exprimées par le nombre de covariables pourrait rendre l’inférence statistique traditionnelle moins attrayante et peu pratique. Par ailleurs, les algorithmes d’apprentissage automatique sont conçus autour de méthodes statistiques modernes pour la réduction des dimensions et la régularisation (e.g. régression Lasso). La phase d’entraînement des algorithmes d’apprentissage automatique est ce qu’on appelle aussi l’estimation des paramètres dans la modélisation statistique et elle n’est pas différente des méthodes d’apprentissage statistique, car elle est fondée sur la validation croisée et le bootstrap.
En résumé, dans une certaine mesure, l’apprentissage statistique et l’apprentissage automatique ne diffèrent pas. Toutefois, dans le domaine de la santé publique, les applications de l’analyse des mégadonnées, notamment la modélisation prédictive, y compris la prévision des séries chronologiques, diffèrent de l’analyse traditionnelle des données biostatistiques en ce qui concerne l’identification et l’évaluation des facteurs de risque. Breiman a fait la distinction entre « les deux cultures » de la modélisation statistique, soit la culture de la modélisation des données et la culture de la modélisation algorithmiqueNote de bas de page 24. Il a soutenu que la théorie statistique n’est pas pertinente si les hypothèses de modélisation ne sont pas respectées dans des situations de données réelles. Cependant, il a également admis que les algorithmes d’apprentissage automatique sont souvent basés sur peu de théorie, et que les hypothèses de modélisation sont remplacées par les propriétés des algorithmes, c.-à-d. si ces derniers convergent et produisent de bonnes prévisions.
D’un point de vue philosophique, l’apprentissage automatique est basé sur une « boîte noire » qui n’est pas ouverte aux interprétations ou aux explications. Dans l’exemple actuel, l’algorithme du RNA (11,1,6)12 comprenait une combinaison non linéaire des données de la série chronologique et 85 paramètresNote de bas de page 23. Par ailleurs, le SARIMA décrit comment les observations antérieures influent sur le déroulement futur d’un processus; cette caractéristique pourrait suggérer des hypothèses causalesNote de bas de page 25. Par conséquent, il n’est pas tout à fait correct de simplement comparer les méthodes de prévision à leurs valeurs prévues ou à leurs mesures de précision, car les approches sont différentes sur le plan philosophique et ne sont pas entièrement comparables; le RNA est un algorithme prédictif, tandis que le SARIMA est un modèle descriptif et prédictif.
Limites
Une des limites de cette étude est le manque d’ajustement pour la population à risque. En effet, la population de l’Ontario augmente régulièrement, mais à un taux annuel inférieur à 0,5 %, ce qui est négligeable dans ce contexte, où la sous-déclaration est plus préoccupante. Aucune tendance des taux mensuels d’incidence de la cryptosporidiose n’a été indiquée par l’approche du SARIMA ou le RNA.
Conclusion
La cryptosporidiose est une maladie fortement saisonnière qui entraîne des périodes favorables et défavorables pour la santé publique. Les méthodes d’apprentissage automatique convenant à la prévision des données chronologiques de la santé publique provenant des systèmes de surveillance sont de plus en plus populaires; il a été démontré qu’elles sont plus précises que les méthodes statistiques traditionnelles. Toutefois, dans cette étude de cas en particulier, le SARIMA a donné lieu à des REQM et à des EAM légèrement inférieures et donc à une plus grande exactitude que le RNA. Les deux approches de prévision ont bien saisi la tendance saisonnière de la cryptosporidiose.
Les études futures devraient utiliser des algorithmes supplémentaires (e.g. forêts d’arbres décisionnels) et évaluer l’exactitude dans différents contextes, soit en utilisant d’autres maladies pour les études de cas, soit en utilisant une approche plus systématique en réalisant des études de simulation.
Déclaration des auteurs
- O. B. a conçu l’examen, recueilli les données et effectué l’analyse des données
- O. B., L. T. W. et S. D. M. ont tous écrit et approuvé le manuscrit
Conflit d’intérêts
Les auteurs déclarent n’avoir aucun conflit d’intérêts.

Cette œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution 4.0 International