Chapitre 2 : Incidence du cancer au Canada : tendances et projections (1983-2032) - PSPMC: Volume 35, supplément 1, Printemps 2015
Chapitre 2: Données et méthodologie
2.1 Données
Les données sur l'incidence du cancer qui ont servi à établir les projections couvrent la période 1983-2007, soit la période la plus récente pour laquelle nous disposions de données pour toutes les régions du Canada. Ces données ont été extraites du Registre canadien du cancer (RCC) pour 1992 à 2007 et du Système national de déclaration des cas de cancer (SNDCC) pour les années antérieures. Alors que le RCC est une base de données axée sur les individus, le SNDCC est une base de données axée sur les événements, qui contient de l'information sur les cas diagnostiqués entre 1969 et 1991. Les cas documentés dans le SNDCC ont été codés selon la Classification internationale des maladies, neuvième révision (CIM-9).Note du fin du texte 6 Nous avons élaboré des projections pour les cancers primitifs envahissants les plus fréquents (incluant le cancer in situ de la vessie, mais excluant le cancer de la peau autre que le mélanome [carcinomes basocellulaire et spinocellulaire]). De façon générale, nous avons défini les cas de cancer en utilisant la Classification internationale des maladies pour l'oncologie, troisième édition (CIM-O-3) et les avons classés selon le registre du Surveillance, Epidemiology, and End Results (SEER) Program – Incidence Site Recode qui figure dans le tableau 2.1.Note du fin du texte 7, Note du fin du texte 8 Les cas extraits du SNDCC portaient les codes de la CIM-9 correspondants. Pour suivre l'évolution de la définition du cancer au fil du temps, nous nous sommes servis des méthodes exposées dans Statistiques canadiennes sur le cancer.Note du fin du texte 1
| Cancer | Siège/type histologiqueTableau 2.1 - Note du fin du texte aCIM-O-3 (Incidence) |
|---|---|
| Cavité buccale | C00–C14 |
| Œsophage | C15 |
| Estomac | C16 |
| Côlon et rectum | C18–C20, C26.0 |
| Foie | C22.0 |
| Pancréas | C25 |
| Larynx | C32 |
| Poumon | C34 |
| Mélanome | C44 (Type 8720–8790) |
| Sein | C50 |
| Col de l'utérus | C53 |
| Corps de l'utérus | C54–C55 |
| Ovaire | C56.9 |
| Prostate | C61.9 |
| Testicule | C62 |
| Rein | C64.9, C65.9 |
| Vessie (y compris les cas in situ) | C67 |
| Système nerveux central | C70–C72 |
| Thyroïde | C73.9 |
| Lymphome de HodgkinTableau 2.1 - Note du fin du texte b | Type 9650–9667 |
| Lymphome non hodgkinienTableau 2.1 - Note du fin du texte b | Type 9590–9596, 9670–9719, 9727–9729 Type 9823, tous les sièges sauf C42.0,C42.1 et C42.4 Type 9827, tous les sièges sauf C42.0,C42.1 et C42.4 |
| Myélome multipleTableau 2.1 - Note du fin du texte b | Type 9731, 9732, 9734 |
| LeucémieTableau 2.1 - Note du fin du texte b | Type 9733, 9742, 9800–9801, 9805, 9820, 9826, 9831–9837, 9840, 9860–9861, 9863, 9866–9867, 9870–9876, 9891, 9895–9897, 9910, 9920, 9930–9931, 9940, 9945–9946, 9948, 9963–9964 Type 9823 et 9827, sièges C42.0,C42.1 et C42.4 |
| Tous les autres cancers | Tous les sièges C00–C80, C97 non mentionnés ci-dessus |
| MésothéliomeTableau 2.1 - Note du fin du texte b | 9050-9055 |
| Sarcome de KaposiTableau 2.1 - Note du fin du texte bTableau 2.1 - Note du fin du texte c | 9140 |
| Intestin grêle | C17 |
| Anus | C21 |
| Vésicule biliaire | C23 |
| Autres sièges de l'appareil digestif | C22.1, C24, C26.8–9, C48 |
| Autres sièges de l'appareil respiratoire | C30–31, C33, C38.1–9, C39 |
| Os et articulations | C40–41 |
| Tissus mous (y compris le cœur) | C38.0, C47, C49 |
| Autres cancers de la peau | C44 excl. 8050:8084, 8090:8110, 8720:8790 |
| Autres sièges de l'appareil génital féminin | C51–52, C57–58 |
| Pénis | C60 |
| Autres sièges de l'appareil génital masculin | C63 |
| Uretère | C66 |
| Autres sièges de l'appareil urinaire | C68 |
| Œil | C69 |
| Autres sièges des glandes endocrines | C37.9, C74, C75 |
| Autres sièges, mal définis et inconnus | Type 9740, 9741, 9750–9758, 9760–9769, 9950–9962, 9970–9989; C76.0–76.8 (type 8000–9589); C80.9 (type 8000–9589); C42.0–42.4 (type 8000–9589); C77.0–C77.9 (type 8000–9589) |
| Tous les cancers | Tous les sièges invasifs |
|
|
Les estimations de population pour l'ensemble du Canada, les provinces et les territoires proviennent des recensements quinquennaux réalisés entre 1981 et 2006. Nous nous sommes servis des estimations intercensitaires élaborées par Statistique Canada pour les années intermédiaires et des estimations postcensitaires pour la période 2007-2010.Note du fin du texte 9 Enfin, pour 2011-2032, nous avons utilisé les projections démographiques établies par Statistique Canada et fondées sur des hypothèses de croissance moyenne (scénario M1).Note du fin du texte 10 Le scénario M1 intègre la croissance moyenne et les tendances passées (1981-2008) de la migration interprovinciale. En ce qui a trait à la population totale, les scénarios de faible et de forte croissance se situent à environ 6 % en dessous et au-dessus du scénario M1, mais cet écart tombe à 3 % pour le groupe des 65 ans et plus.
Les données sur l'incidence du cancer et les estimations démographiques sont présentées sommairement par groupe d'âge de cinq ans (0-4, 5-9, …, 80-84, 85+) et par période de diagnostic de cinq ans (1983-1987, 1988-1992, 1993-1997, 1998-2002, 2003-2007) selon le sexe et la zone géographique (Colombie-Britannique, Prairies [Alberta, Saskatchewan et Manitoba, considérées individuellement ou ensemble], Ontario, Québec, région de l'Atlantique [Nouveau-Brunswick, Île-du-Prince-Édouard, Nouvelle-Écosse et Terre-Neuve-et-Labrador, considérées individuellement ou ensemble] et Nord [Yukon, Territoires du Nord-Ouest et Nunavut]). De même, les projections démographiques ont été regroupées en cinq périodes quinquennales (2008-2012, 2013-2017, 2018-2022, 2023-2027, 2028-2032). Les projections de l'incidence du cancer de la prostate ont été établies à partir des données annuelles de 1994 à 2007. Nous avons calculé les taux pour chaque catégorie en divisant le nombre de cas de cette catégorie (c.-à-d. type de cancer, sexe, région, période et groupe d'âge) par les effectifs de population correspondants. Les taux selon l'âge ont été normalisés à partir de la population du Canada de 1991 (tableau 2.2) au moyen de la méthode directeNote du fin du texte 11, ce qui a fourni les taux d'incidence normalisés selon l'âge (TINA).
| Groupe d'âge | Population (pour 100 000) |
|---|---|
| 0–4 | 6946 |
| 5–9 | 6945 |
| 10–14 | 6803 |
| 15–19 | 6850 |
| 20–24 | 7502 |
| 25–29 | 8994 |
| 30–34 | 9240 |
| 35–39 | 8339 |
| 40–44 | 7606 |
| 45–49 | 5954 |
| 50–54 | 4765 |
| 55–59 | 4404 |
| 60–64 | 4233 |
| 65–69 | 3857 |
| 70–74 | 2966 |
| 75–79 | 2213 |
| 80–84 | 1360 |
| 85+ | 1024 |
| Total | 100 000.00 |
|
Remarque : La distribution de la population canadienne est fondée sur les estimations finales de la population canadienne au 1er juillet 1991 après le recensement, rajustée pour le sous-dénombrement lors du recensement. La répartition par âge de la population a été pondérée et normalisée. Source des données : Direction de la statistique démographique, Statistique Canada. |
|
2.2 Méthodologie
2.2.1 Méthodes de projection
On estime généralement les tendances futures des taux d'incidence du cancer en extrapolant les tendances passées à l'aide de modèles statistiques. Un modèle statistique sert à formuler la relation entre les facteurs de risque et les taux de cancer, et on obtient des projections en intégrant les périodes futures dans l'équation du modèle.
Il existe plusieurs méthodes permettant d'anticiper quel sera le fardeau du cancer. Elles diffèrent par le type de modèle utilisé, par le choix des données servant à l'ajustement du modèle et par la méthode d'extrapolation des éléments du modèle sur les périodes futures. Le type de modèle varie de la régression linéaire simple – ou de la régression log-linéaire – des taux ou des comptages selon l'âge par rapport au tempsNote du fin du texte 2, Note du fin du texte 12, Note du fin du texte 13 au modèle âge-période-cohorte (APC).Note du fin du texte 11, Note du fin du texte 14, Note du fin du texte 15 Dans les modèles APC, les effets de l'âge, de la période et de la cohorte peuvent être traités de différentes façons, que ce soit par des modèles linéaires généralisésNote du fin du texte 16, Note du fin du texte 17 et leurs dérivés, par la méthode Nordpred, qui repose sur une fonction échelon sur des intervalles de cinq ansNote du fin du texte 3, Note du fin du texte 15, par les modèles additifs généralisésNote du fin du texte 18, Note du fin du texte 19 avec méthodes de lissage polynomialNote du fin du texte 15, Note du fin du texte 20 ou splineNote du fin du texte 21 ou encore par les modèles bayésiensNote du fin du texte 22 avec simulation de Monte Carlo par chaîne de Markov (MCMC).Note du fin du texte 23 La fonction lien est soit la fonction exponentielle ordinaireNote du fin du texte 11, Note du fin du texte 14, Note du fin du texte 22, soit la fonction puissance de forme non canonique.Note du fin du texte 3, Note du fin du texte 15 Nous ajustons le modèle à toutes les données disponibles ou à un sous-ensemble de ces données, puis nous soumettons ce modèle à un test de qualité de l'ajustement.Note du fin du texte 3, Note du fin du texte 15 Les hypothèses utilisées pour l'extrapolation des tendances observées sont les suivantes : taux courants maintenus fixes dans les années à venirNote du fin du texte 24, maintien de la tendance passée générale Note du fin du texte 2, Note du fin du texte 22, extrapolation de la tendance la plus récente seulementNote du fin du texte 3Note du fin du texte15 et ajustement du degré d'influence probable de la tendance observée sur l'avenir.Note du fin du texte 3Note du fin du texte 15 Afin de décrire le plus exactement possible le fardeau que représentera le cancer dans l'avenir, nous avons eu recours à ces principaux modèles pour élaborer des projections des taux courants comme on aurait pu le faire il y a 15 ou 20 ans à partir des séries de données à long terme du Canada, puis nous avons comparé ces taux projetés avec les taux observés et nous en avons déduit une méthode de modélisation centrée sur le cancer. Cette méthode multidimensionnelle intègre les modèles suivants et elle en combine les points forts.
Les modèles de projection courants mettent en rapport l'incidence et les trois variables temporelles intrinsèquement interdépendantes, soit l'âge au moment du diagnostic (âge), l'année du diagnostic (période) et l'année de naissance (cohorte). Le modèle APC NordpredNote du fin du texte 3Note du fin du texte 15 utilise la fonction lien puissance-5 au lieu de la fonction logarithmique classique pour réduire les variations exponentielles, résume par un terme de dérive les tendances linéaires des variables période et cohorte par rapport à l'ensemble des données observées, puis atténue arithmétiquement la dérive dans la période à venir afin d'amortir l'effet des tendances antérieures dans l'avenir et, enfin, il choisit les données devant servir à l'ajustement du modèle, ainsi que le terme de dérive pour les extrapolations. Le modèle Nordpred avec son paramètre standard et la modification des paramètres est la principale méthode de projection utilisée dans cette monographie. En l'absence d'effets de cohorte, nous avons eu recours à un modèle Nordpred sans terme de cohorte. Lorsqu'il y avait trop peu d'observations pour estimer correctement les paramètres du modèle par la méthode Nordpred ou que les projections établies à l'aide de Nordpred semblaient douteuses pour des raisons d'ordre biologique ou clinique, soit nous avons opté pour les modèles APC bayésiensNote du fin du texte 22 ou les sous-modèles, avec diverses distributions a priori, ou la méthode de la moyenne de cinq ans, soit nous avons appliqué un ajustement proportionnel aux estimations nationales pour obtenir des estimations pour une région. Les modèles bayésiens permettent d'estimer les taux selon l'âge à partir de la distribution a posteriori au moyen d'un échantillonnage par itération, tandis que le modèle de la moyenne de cinq ans suppose que les taux selon l'âge courants demeureront inchangés dans l'avenir. En outre, nous nous sommes servis du modèle puissance-5 d'établissement des tendances selon l'âge, que nous avons ajusté aux données les plus récentes pour la projection de l'incidence du cancer de la prostate, pour réduire l'effet du dépistage de l'antigène prostatique spécifique (APS) sur la tendance à long terme.
Tous les modèles de projection à long terme reposent sur l'hypothèse d'une continuité des tendances passées des taux selon l'âge, mais à divers degrés. Nous décrivons ci-dessous les différents modè les et nous en faisons la comparaison pour déterminer quels sont les « meilleurs » modèles selon les circonstances.
2.2.1.1 Modèles de projection
2.2.1.1.1 Modèles Nordpred Power 5 – modèles linéaires généralisés modifiés (NP_ADPC et NP_ADP)
La méthode Nordpred a été développée dans le cadre d'une analyse exhaustive des tendances du cancer dans les pays nordiques.Note du fin du texte 3, Note du fin du texte 25 Elle repose sur un modèle APC qui se présente sous la forme d'une régression de Poisson ordinaireNote du fin du texte 14, Note du fin du texte 16, Note du fin du texte 26, mais il a été démontré que cette méthode produit des prévisions plus réalistes, notamment en ce qui concerne la projection à long termeNote du fin du texte 15, Note du fin du texte 27. Elle compte maintenant parmi les méthodes le plus souvent utilisées à l'échelle mondiale pour établir des projections sur le cancer.Note du fin du texte 28, Note du fin du texte 29, Note du fin du texte 30, Note du fin du texte 31 Dans le modèle standard, la relation log-linéaire entre le taux d'incidence et les covariables permet d'établir des prévisions indiquant des taux qui augmentent de façon exponentielle avec le temps. Or Nordpred utilise comme fonction lien la fonction puissance au lieu de la fonction logarithmique pour atténuer cette croissance. Dans ce contexte, la fonction puissance est une approximation de la fonction logarithmique qui est fondée sur la théorie de la transformation (exponentielle) de Box-Cox, où λ→ 0lim xλ = log(x). Le modèle Nordpred est défini ainsi :


où Rap est le taux d'incidence pour le groupe d'âge a à la période de calendrier p, c'est-à-dire le nombre moyen, µap, de casap divisé par la taille de la population correspondante, nap; Aa, Pp et Cc sont les composantes non linéaires du groupe d'âge a, de la période p et de la cohorte c respectivement, et D est le paramètre de dérive linéaire commun de la période et de la cohorteNote du fin du texte 26. On détermine une cohorte en soustrayant l'âge de la période : c = A +p – a, où A est le nombre de groupes d'âge (c.-à -d. 18).
Afin d'assurer un bon ajustement des données au modèle, on détermine dans le logiciel Nordpred le nombre de périodes de cinq ans sur lesquelles seront fondées les projections en éliminant successivement les périodes antérieures au moyen d'un test de qualité de l'ajustement. Pour ce qui est de l'extrapolation du modèle sur les périodes futures, on envisage deux méthodes au lieu de supposer simplement la continuité de la tendance générale observée. Premièrement, le logiciel détermine si la tendance moyenne de l'ensemble des valeurs observées, ou la pente relative aux observations des 10 dernières années, tiendra lieu de terme de dérive (D) devant faire l'objet d'une projection. Pour ce faire, le logiciel effectue un test de déviation par rapport à la tendance linéaire. Si la tendance sur toute la période d'observation s'écarte significativement de la linéarité, on ne retiendra que la tendance des 10 dernières années pour la projection. Le logiciel comprend l'option « recent » qui permet de choisir entre l'utilisation de la tendance moyenne (recent = F) ou l'utilisation de la tendance des 10 dernières années (recent = T) pour la projection. Deuxièmement, afin d'atténuer l'effet des tendances courantes dans les périodes futures, on utilise l'option « cut trend » (ou « drift »), qui consiste en un vecteur de proportions permettant d'indiquer dans quelle mesure tronquer la tendance estimée pour chaque période de projection de cinq ans. Dans Nordpred, des pourcentages de réduction progressive du paramètre de dérive de 25, 50, 75 et 75 % dans les deuxième, troisième, quatrième et cinquième périodes quinquennales respectivement servent de valeur de troncation par défaut.Note du fin du texte 3, Note du fin du texte 25
À la recherche de méthodes de projection exacte pour cette étude, nous avons comparé les modèles puissance-5 et les modèles de Poisson (en utilisant la fonction lien logarithmique au lieu de la fonction lien puissance dans l'équation NP_ADPC) avec le modèle Nordpred recommandé et ses différentes versions. Nous avons modifié l'option « cut trend » de Nordpred pour pour réduire ou augmenter les impacts des tendances actuelles dans les périodes à venir.
L'étude exigeant un minimum de 5 cas dans chaque période quinquennale pour chaque groupe d'âge, nous nous sommes servis, pour calculer les taux futurs pour les groupes d'âge n'atteignant pas cette limite, du nombre moyen de cas dans les deux dernières périodes. Si nous avions fixé le seuil à 10 cas, comme dans le rapport sur les pays nordiques pour la plupart des situationsNote du fin du texte 3, nous aurions obtenu des taux moyens pour un plus grand nombre de groupes d'âge mais en réduisant l'effet des tendances courantes. Par conséquent, le choix du minimum de 5 visait le compromis entre une estimation non biaisée de la tendance fondamentale et une forte erreur d'estimation.
En plus du modèle intégral ADPC, nous avons pensé utiliser un modèle âge-dérive-période (ADP) avec des fonctions liens puissance-5 pour les cancers dont le nombre annuel moyen de cas est inférieur à 50 pour les cinq dernières années observées, compte tenu de l'absence d'effets de cohorte vérifiée par un test de signification :
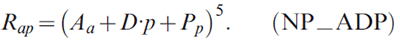
Le modèle ADP a été utilisé pour les cancers rares en Islande dans une analyse de l'évolution du cancer dans les pays nordiques.Note du fin du texte 3
2.2.1.1.2 Méthode bayésienne de Monte Carlo par chaîne de Markov
Nous avons appliqué un cadre bayésien, plutôt que la méthode du maximum de vraisemblance, au modèle APC ou au sous modèle. La méthode bayésienne incorpore des connaissances a priori dans le modèle pour en tirer une distribution a posteriori et elle utilise des approximations MCMCNote du fin du texte 22, Note du fin du texte 23 pour l'inférence (estimations de paramètres). Nous avons envisagé d'utiliser cette méthode lorsque le nombre annuel moyen de cas de cancer était égal ou inférieur à 10 pour les cinq dernières années observées (c.-à-d. lorsque les observations sont trop peu nombreuses pour que l'on puisse estimer correctement les paramètres du modèle par la méthode Nordpred) ou que les projections établies au moyen de Nordpred semblaient peu plausibles. Nous avons donc envisagé deux approches bayésiennes.
2.2.1.1.2.1 Modèle APC bayésien autorégressif à distribution a priori – méthode de Bray (B_APC)
Pour ce qui est du modèle de Poisson APC classiqueNote du fin du texte 26, Bray a spécifié un modèle a priori autorégressif du second ordre pour lisser les effets d'âge, de période et de cohorte et extrapoler les effets de période et de cohorte.Note du fin du texte 22, Note du fin du texte 23 Le modèle est exprimé comme suit :

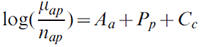
À supposer que nous établissons des projections pour N périodes sur la base d'observations de P périodes, nous avons en tout C (= A+P − 1) cohortes. Dans le modèle Nordpred, une cohorte c se calcule comme suit : c = A + p − a. Les distributions a priori sont définies ainsi :
- pour les effets d'âge (A)

- pour les effets de période (P + N) :

- pour les effets de cohorte (C + N) :

Les paramètres de variance τA, τP et τC (qui déterminent le lissage des effets d'âge, de période et de cohorte respectivement) suivent tous la même distribution a priori (gamma),

On calcule les taux ajustés et les taux projetés en combinant les effets d'âge, de période et de cohorte simulés suivant la formule
Rap = exp(Aa + Pp + Cc)
Trois chaînes MCMC ont été conduites avec une période initiale de 50 000 itérations (« burn in »). Les estimations de paramètres (médianes a posteriori) ont été établies après 50 000 autres itérations pour chaque chaîne, à laquelle on a soustrait un échantillon tous les 30 (N = 150 000 échantillons). L'évaluation de la convergence des chaînes s'est faite au moyen de la statistique de Gelman-Rubin, d'un examen de l'autocorrélation d'échantillon et d'une inspection visuelle. La modélisation bayésienne a été exécutée entiè rement sur WinBUGS (Windows Version of Bayesian inference Using Gibbs Sampling)Note du fin du texte 32 (pour plus de détails sur ce logiciel, se référer à un autre ouvrageNote du fin du texte 33).
2.2.1.1.2.2 Modèle âge-période bayésien utilisant les coefficients nationaux comme moyennes des distributions a priori pour les projections régionales (B_AP)
Pour garantir la stabilité des estimations régionales, nous avons supposé pour les paramètres régionaux des distributions initiales ou a priori basées sur les données nationales, que nous avons ensuite actualisées au moyen des données régionales réelles. Le modèle est exprimé comme suit :

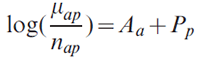
Ce modèle a tout d'abord servi à estimer les coefficients des variables âge et période au niveau national, désignés par Âa et ˆPp (dénoté dans la formule par la lettre P avec un accent circonflexe) respectivement. Nous avons ensuite défini pour les effets d'âge Aa et de période Pp régionaux des distributions a priori normales dont la moyenne est égale aux estimations nationales correspondantes,
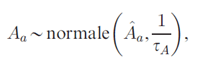
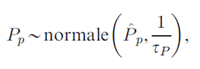
où les paramètres de variance τA, τP suivent tous deux la même distribution a priori (gamma),

À l'instar de Spiegelhalter et ses collaborateurs Note du fin du texte 34, nous avons imposé les restrictions habituelles au premier effet d'âge (A1 = 0) pour faciliter les calculs.
2.2.1.1.3 Modèle de la moyenne de cinq ans (AVG)
Le modèle de la moyenne de cinq ans suppose que les taux d'incidence moyens du cancer selon l'âge pour les cinq dernières années observées demeureront constants dans les prochaines années, de sorte que le nombre de cas de cancer dans l'avenir ne dépendra que des changements démographiques. Les taux projetés sont calculés au moyen de la formule suivante :
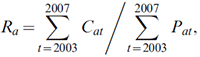
où Radésigne le taux d'incidence pour le groupe d'âge a, Cat, le nombre de cas pour le groupe d'âge a dans l'année t, et Pat, l'effectif du groupe d'âge a dans l'année t.
2.2.1.1.4 Méthode de l'ajustement proportionnel – projections régionales obtenues par l'ajustement (scaling down) des projections nationales (SD)
Pour les cancers dont le nombre annuel moyen de cas dans une région donnée est inférieur à 10 pour les cinq dernières années observées, nous avons déterminé le nombre de cas selon l'âge par l'ajustement des estimations nationales (selon une méthode modifiée utilisée dans le registre du cancer de la Norvège).Note du fin du texte 35 Posons w comme étant la différence relative des moyennes des TINA des cinq dernières années d'observations entre la région et le pays entier, c'est-à-dire
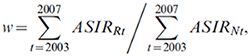
alors, le taux d'incidence du cancer dans la région R, pour le groupe d'âge a et la période p, est défini par
RRap = RNap * w = (CNap / PNap) * w,
où RNap, CNap et PNap désignent respectivement, pour le groupe d'âge a dans la période p, le taux d'incidence du cancer, le nombre de cas et l'effectif de population à l'échelle nationale. Par exemple, si la région considérée présente des taux d'incidence inférieurs de 5 % à la moyenne nationale pour les cinq dernières années d'observations, les taux selon l'âge pour cette région sont abaissés de 5 % dans chaque période future. Nous pouvons donc déterminer le nombre de nouveaux cas de cancer dans la région au moyen de la formule
CRap = RRap * PRap.
2.2.1.1.5 Modèle puissance-5 d'établissement des tendances selon l'âge ajusté aux données annuelles pour la projection à court terme de l'incidence du cancer de la prostate (ADa)
Depuis le début des années 1990, les tendances de l'incidence du cancer de la prostate sont influencées par le surdiagnostic (c'est-à -dire la détection d'un cancer latent qui n'aurait jamais été diagnostiqué en l'absence de dépistage) à cause de la diffusion rapide du test de l'APS.Note du fin du texte 36 Les projections établies au moyen de l'analyse par période de Nordpred semblent peu plausibles. Nous avons donc ajusté un modèle puissance-5 d'établissement des tendances selon l'âge fondé sur des données annuelles aux observations d'au moins huit années entre 1994 et 2007 afin d'élaborer des projections de l'incidence du cancer de la prostate pour les cinq (2008-2012) ou dix années suivantes (2008-2017) : Rap = (Aa + Da.p)5, où Da est le paramètre de pente pour le groupe d'âge a, qui tient compte de la différence de tendance entre les groupes d'âge. Ce modèle tient compte aussi de la valeur « pic » de 2001. Un autre pic avait été enregistré en 1993, mais cette dernière année est exclue du modèle.
2.2.1.2 Comparaison des modèles
Nous avons ajusté les modèles de projection décrits ci-dessus aux données sur le nombre de nouveaux cas de cancer pour la période de 1972 à 1991 et avons utilisé ces modèles pour estimer le nombre annuel moyen de cas de cancer pour les périodes quinquennales entre 1992 et 2011. Les projections sont ventilées selon le sexe, le groupe d'âge, la zone géographique (ainsi que le Canada dans son ensemble) et le type de cancer (voir le tableau 2.1). Le Québec a été exclu de cette analyse en raison de la qualité douteuse des données avant 1983.Note du fin du texte 37, Note du fin du texte 38
Étant donné que le cancer de la prostate explique près du tiers de tous les nouveaux cas de cancer chez les hommes au Canada, l'effet du dépistage par l'APS s'observe clairement dans les données sur l'incidence de « tous les cancers combinés » chez les hommes. Par conséquent, nous avons fait les comparaisons de modèles tantô t sur la base de « tous les cancers combinés », tantôt sur celle de « tous les cancers, sauf le cancer de la prostate », selon le cas.
Nous avons comparé le nombre annuel moyen estimé de cas de cancer avec les valeurs observées. Nous avons calculé l'écart relatif absolu médian entre les valeurs estimées et observées, |estimation 2 observation|/observation, afin d'examiner la tendance de chaque modèle à surestimer ou à sous-estimer le nombre réel de cas de cancer. Pour les cancers rares, nous avons fondé nos comparaisons sur l'écart absolu. Nous avons aussi comparé les erreurs de prévision médianes de chaque modèle selon des combinaisons du type de cancer, de la zone géographique et du sexe par durée de projection. Seules les combinaisons pour lesquelles les modèles ont établi des projections ont été prises en compte dans l'exercice. Nous nous sommes servis du test de FriedmanNote du fin du texte 39 pour déterminer s'il existe une différence statistique entre les médianes calculées pour les différents modèles de projection. En plus de calculer l'erreur de prévision pour l'ensemble des types de cancer, nous avons comparé la performance des modèles pour chaque type de cancer pris séparément, par sexe et par zone géographique.
2.2.1.3 Validation des projections et rectification
Le choix des modèles s'est fait sur la base d'une évaluation des modèles et d'une mise en commun des résultats de cette évaluation et de ceux publiés dans d'autres études. Or un modèle fondé sur des cohortes associées à des périodes passées plus lointaines peut générer des prévisions inexactes s'il est appliqué aux cohortes actuelles. En raison du trop petit nombre d'ensembles de données à long terme dont nous disposons pour valider les modèles sélectionnés, nous avons examiné les projections établies par ces modèles en nous servant de nos connaissances sur la qualité des données, les tendances des taux de cancer dans différentes régions, les facteurs de risque ou les interventions pour nous assurer de la qualité des estimations. Lorsque les tendances estimées semblaient peu plausibles, nous avons mis à profit ces connaissances pour rectifier les méthodes d'extrapolation des modèles ajustés, ou avons eu recours aux simulations bayésiennes en remplacement des modèles linéaires généralisés. Des ajustements de ce genre ont dû être faits dans les cas suivants : pour tous les cancers combinés chez les hommes à l'Île-du-Prince-Édouard, en Saskatchewan et en Alberta et chez les femmes en Ontario, au Manitoba et en Alberta, pour le lymphome non hodgkinien (LNH) chez les femmes au Nouveau-Brunswick, pour les myélomes multiples chez les hommes dans la région de l'Atlantique et au Nouveau-Brunswick et chez les femmes en Ontario et en Colombie-Britannique et pour le cancer de la glande thyroïde dans toutes les provinces sauf le Manitoba, la Saskatchewan et la Colombie-Britannique.
2.2.1.4 Modèles choisis selon le type de cancer
Nous avons utilisé les méthodes de projection suivantes dans cette monographie.
- Cancers courants (nombre annuel moyen de cas pour les cinq dernières années d'observation, série nationale ou régionale, N > 50) : modèle NP_ADPC avec des valeurs « recent » et « drift » variées, sauf dans le cas des myélomes multiples chez les hommes dans la région de l'Atlantique, où on a utilisé le modèle B_APC parce que les projections du modèle NP_ADPC semblaient sujettes à caution.
- Cancers moins courants (10 < N ≤ 50): modè le NP_ADPC ou NP_ADP (selon la signification de l'effet de cohorte et la comparaison avec les résultats du modè le AVG), avec des valeurs « recent » et « drift » variées. Dans notre évaluation des modèles et d'autres étudesNote du fin du texte 27, le modèle AVG avec effet d'âge seulement s'avère la meilleure méthode pour les cancers rares, et il a été utilisé dans des rapports récents.Note du fin du texte 35 Compte tenu de cela, nous avons utilisé, entre NP_ADPC et NP_ADP, celui des deux dont les projections se rapprochaient le plus des résultats du modèle AVG, au lieu de nous limiter à une extrapolation linéaire du taux moyen de cinq ans dans l'avenir. Une exception a été l'utilisation du modèle B_APC pour le myélome multiple chez les hommes au Nouveau-Brunswick.
- Cancers rares (N ≤ 10) : modèle NP_ADPC, NP_ADP, B_APC, B_AP ou SD, à savoir celui dont les projections se rapprochaient le plus des résultats du modèle AVG.
- Cancer de la prostate : modèle ADa + AVG, défini comme suit :
- l'utilisation du modèle ADa permet d'établir des projections pour les cinq premières années, puis
- l'utilisation des taux moyens selon l'âge fondés sur les projections sur cinq ans permet d'estimer le nombre de cas de cancer de la deuxième à la cinquième période quinquennale.
- « Tous les cancers » chez les hommes : pour calculer les estimations de l'incidence, nous avons additionné les estimations relatives au cancer de la prostate et les estimations relatives à « tous les cancers moins celui de la prostate », suivant le modèle NP_ADPC.
Le tableau 2.3 décrit les modèles de projection sélectionnés en fonction du type de cancer, du sexe et de la zone géographique.
| Cause | Modèle | |||
|---|---|---|---|---|
| B_APTableau 2.3 - Note du fin du texte a | B_APCTableau 2.3 - Note du fin du texte a | SDTableau 2.3 - Note du fin du texte a | NP_ADPTableau 2.3 - Note du fin du texte a | |
| Cavité buccale | Î.-P.-É./F, TC/H+F | Man./F | ||
| Œsophage | TC/H, T.-N.-L./F | Î.-P.-É.+TC/F | N.-É./F | |
| Estomac | Î.-P.-É./H | TC/F | Î.-P.-É./F, TC/H | N.-B./F |
| Côlon et rectum | Î.-P.-É./F | TC/H+F | ||
| Foie | N.-É./F, TC/H | Î.-P.-É.+T.-N.-L./H+F, N.- B.+Sask.+TC/F | Man.+Sask./H, AT/H+F | |
| Pancréas | TC/H+F | Î.-P.-É./H+F | T.-N.-L./F | |
| Larynx | Î.-P.-É./F, TC/H | Î.-P.-É./H, N.-É.+N.- B.+Man.+Sask./F | T.-N.-L.+TC/F | AT/F |
| Mélanome | TC/H+F | |||
| Sein | TC/F | |||
| Col de l'utérus | Î.-P.-É./F, TC/F | Man./F | ||
| Corps de l'utérus | TC/F | |||
| Ovaire | TC/F | Î.-P.-É./F | ||
| Testicule | Î.-P.-É.+T.-N.-L.+TC/H | N.-É.+N.-B.+Man./H | ||
| Rein | Î.-P.-É./F | TC/F | TC/H | Î.-P.-É./H, T.-N.-L./H+F |
| Vessie | Î.-P.-É.+TC/F, TC/H | T.-N.-L./F | ||
| Système nerveux central | Î.-P.-É.+TC/H+F | N.-É./H, N.-B.+T.-N.-L.+Sask./F, Man./H+F | ||
| Thyroïde | Î.-P.-É./H | Î.-P.-É./F | TC/H+F | N.-É./H, Sask./F |
| Lymphome de Hodgkin | N.-B./F | Î.-P.-É.+T.-N.-L.+TC/H+F | N.-B.+Alb.+AT/H, C.-B./F, N.-É.+Man.+Sask./H+F | |
| Lymphome non hodgkinien | Î.-P.-É./F, TC/H+F | Î.-P.-É./H | T.-N.-L./H+F, AT+N.-É.+N.-B./F | |
| Myélome multiple | AT+N.-B./H, Î.-P.-É./F | Î.-P.-É./H, T.-N.-L./F, TC/H+F | N.-É.+Man.+Sask./H+F, T.-N.-L./H | |
| Leucémie | Î.-P.-É./H, TC/F | Î.-P.-É./F | TC/H | T.-N.-L./H+F |
| Tous les autres cancers | Î.-P.-É./F | TC/F | ||
|
Abréviations : C.-B. = Colombie-Britannique, Alb. = Alberta, Sask. = Saskatchewan, Man. = Manitoba, N.-B. = Nouveau-Brunswick, N.-É. = Nouvelle-Écosse,Î.-P.-É. = Île-du-Prince-Édouard, T.-N.-L. = Terre-Neuve-et-Labrador, TC = Tous les territoires (Yukon, Territoires du Nord-Ouest et Nunavut) et AT = Toutes les provinces de l'Atlantique (Î.-P.-É., N.-É., N.-B. et T.-N.-L.). Remarque : L'abréviation située avant la barre oblique (/) correspond à la zone géographique; la lettre H ou F située après la barre oblique correspond à « hommes » ou « femmes ». Par exemple, Î.-P.-É.+TC/H+F signifie qu'on a utilisé le modèle SD chez les hommes et les femmes de l'Î.-P.-É. et des TC pour prévoir les cas de cancers du système nerveux central.
|
||||
2.2.2 Autres méthodes d'analyse
2.2.2.1 Analyse de régression Joinpoint
Nous avons évalué les tendances observées (1986-2007) au moyen d'une régression JoinpointNote du fin du texte 40, Note du fin du texte 41, qui consiste à ajuster une série de droites raccordées sur une échelle logarithmique aux tendances des TINA. Les tendances de l'incidence sont exprimées par la variation annuelle en pourcentage. Les modèles rendent compte des erreurs-types estimées des TINA. Les tests de signification ont été effectués à l'aide de la méthode de permutation de Monte Carlo. Enfin, la pente estimée au moyen de cet ajustement a été de nouveau transformée pour exprimer un pourcentage d'augmentation ou de diminution annuelle du taux d'incidence.
Pour déceler une tendance nouvelle, il fallait au moins cinq années de données avant et après un point de retournement, c'est-à-dire une année où la variation annuelle en pourcentage a changé de manière significative. Ainsi, le point de retournement le plus récent est 2003. Comme l'indiquent les figures 3.1 et 3.2, si aucun point de retournement n'était détecté au cours de la période 1998-2007, nous calculions la variation annuelle en pourcentage en appliquant à cette période un modèle ajusté. Si, au contraire, un point de retournement était détecté au cours de cette décennie, nous calculions la variation annuelle en pourcentage à partir de la tendance dans la dernière partie. Les deux figures précitées indiquent l'année du point de retournement et la variation annuelle en pourcentage pour les années suivant le point de retournement.
2.2.2.2 Rôle des variations du risque de cancer, de la croissance démographique et de la structure par âge de la population dans l'évolution de l'incidence
La figure 3.4 décrit l'effet relatif des variations du risque de cancer, de la croissance démographique et du vieillissement de la population sur le nombre total de nouveaux cas. Les séries sont définies comme suit (nous avons calculé le taux annuel d'incidence normalisé selon l'âge en utilisant comme pondération la répartition de la population annuelle moyenne dans la période 1983-1987 pour les hommes ou les femmes) :Note du fin du texte 1
- La série initiale (ligne rouge) représente le nombre annuel moyen observé de nouveaux cas de cancer entre 1983 et 1987 pour les hommes ou les femmes.
- La ligne noire inférieure représente le nombre annuel moyen de nouveaux cas de cancer qui se seraient déclarés dans chaque période si la taille et la composition de la population annuelle moyenne étaient demeurées les mêmes que durant la période 1983-1987. Cette série mesure donc l'effet des variations du risque de cancer. On la calcule en multipliant la population annuelle moyenne entre 1983 et 1987 par le TINA.
- La ligne noire médiane représente le nombre annuel moyen de nouveaux cas de cancer qui se seraient déclarés si la structure par âge de la population annuelle moyenne était demeurée la même que durant la période 1983-1987. Cette série mesure donc l'effet des variations du risque de cancer et de la croissance démographique. On la calcule en multipliant la population annuelle moyenne par le TINA.
- La ligne noire supérieure représente le nombre annuel moyen total de nouveaux cas de cancer qui se sont déclarés (estimations projetées en date de 2008) dans chaque période chez les hommes ou les femmes; cette série mesure l'effet combiné des variations du risque de cancer, de la croissance démographique et du vieillissement de la population.
2.3 Présentation des résultats
Dans cette monographie, alors que les figurent décrivent les tendances temporelles à plus long terme des TINA pour chaque siège de cancer pour des niveaux d'agrégation géographique supérieurs, les tableaux présentent le nombre de nouveaux cas de cancer et les taux d'incidence pour toutes les provinces et tous les territoires à compter de la dernière période d'observation (2003-2007). Les nombres de cas présentés dans les tableaux et les figures sont des nombres annuels moyens. Tous les TINA ont été calculés pour 100 000 années-personnes.
Les figures présentent, pour chaque type de cancer, les TINA passés et projetés pour illustrer les tendances temporelles des taux et les différences selon le sexe et le groupe d'âge (< 45, 45-54, 55-64, 65-74, 75-84, 85+) et selon la région (Colombie-Britannique, Prairies, Ontario, Québec, région de l'Atlantique et Canada dans son ensemble). Le Nord n'est pas représenté ici en raison des faibles effectifs. Dans les figures 3.8 à 3.10, le nombre de cas a été arrondi à la centaine près.
Les tableaux pour les hommes et pour les femmes présentent le nombre annuel moyen de cas et les TINA, observés (2003-2007) et projetés, selon le groupe d'âge décennal et la province ou le territoire. Le nombre de cas a été arrondi au multiple de 5 le plus proche. Les nombres ayant été arrondis individuellement, il est possible que les totaux dans les tableaux ne concordent pas.
Le chapitre 3 brosse un tableau des tendances observées et projetées pour tous les cancers combinés, tandis que le chapitre 4 ventile cette information selon le type de cancer. Les cancers ont été classés selon les codes CIM-O-3.