ARCHIVED – Social Capital and Employment Entry of Recent Immigrants to Canada
10. Appendix B
Log likelihood test of panel-level variance component in the random effects model
Assuming that the unobserved individual effects zi in the general model are unrelated to the observed explanatory variables xit: Cov (xit, zi) =0, t=1, 2, …, T, so that the conditional distribution f (zi| xit) is independent on xit, I get the random effects model:
![]() i=1,…, n, t=1,…, Ti.
i=1,…, n, t=1,…, Ti.
E (vit | xit) =0,
where ![]()
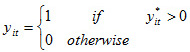
and ![]() are iid logistic distributed with mean zero and variance
are iid logistic distributed with mean zero and variance ![]() , independently of zi.
, independently of zi.
The proportion of the total variance contributed by the panel-level (i.e. subject level) variance component is ![]() . When
. When ![]() is zero, the panel-level variance component is unimportant, and the panel estimator is not different from the pooled estimator. A likelihood-ratio test of the null hypothesis that
is zero, the panel-level variance component is unimportant, and the panel estimator is not different from the pooled estimator. A likelihood-ratio test of the null hypothesis that ![]() equals zero compares the pooled estimator with the random effects estimator. In our analysis, a likelihood ratio test of this is included at the bottom of the Stata output of the random effects estimation (e.g. see following output for the random estimation of the employment probability of male immigrants):
equals zero compares the pooled estimator with the random effects estimator. In our analysis, a likelihood ratio test of this is included at the bottom of the Stata output of the random effects estimation (e.g. see following output for the random estimation of the employment probability of male immigrants):
> /*Random-effects logit regression*/
> xtlogit em swpa swsd refugee other
> age agesq married nkid nkid4_14 nykid
> Atlantic Quebec Prairies BC noncma
> bregion1 bregion3-bregion5
> min1-min8
> ed1-ed3 ed5 insch
> Eng Fre
> prework lengthca lengthsq
> jobarranged visitbf workbf studybf
> spwkcur spwage relative nr rlnear fsdensity
> friend frnear newfri nfoutwk frdiv frdensity
> pgo ngo godiv godensity govo
> if male==1 & lf==1, i(id) re;
Random-effects logistic regression Number of obs = 7632
Group variable (i): id Number of groups = 4239
Random effects u_i ~ Gaussian Obs per group: min = 1
avg = 1.8
max = 2
Wald chi2(58) = 831.86
Log likelihood = -3839.4768 Prob > chi2 = 0.0000
| em | Coef. | Std. Err. | z | P>z | [95% Conf. Interval] | |
|---|---|---|---|---|---|---|
| swpa | -.1475564 | .1960424 | -0.75 | 0.452 | -.5317926 | .2366797 |
| swsd | -.3746873 | .2039548 | -1.84 | 0.066 | -.7744313 | .0250567 |
| refugee | -.8966477 | .199611 | -4.49 | 0.000 | -1.287878 | -.5054172 |
| other | .0392413 | .2225304 | 0.18 | 0.860 | -.3969102 | .4753928 |
| age | .133618 | .0283932 | 4.71 | 0.000 | .0779684 | .1892677 |
| agesq | -.2100867 | .0344855 | -6.09 | 0.000 | -.2776769 | -.1424964 |
| married | -.0579413 | .1197569 | -0.48 | 0.629 | -.2926605 | .1767778 |
| nkid | .0307523 | .0682012 | 0.45 | 0.652 | -.1029196 | .1644242 |
| nkid4_14 | -.1334155 | .0772561 | -1.73 | 0.084 | -.2848346 | .0180037 |
| nykid | -.0653268 | .1039146 | -0.63 | 0.530 | -.2689957 | .1383421 |
| Atlantic | -.2547173 | .4284288 | -0.59 | 0.552 | -1.094422 | .5849877 |
| Quebec | -1.00029 | .1457717 | -6.86 | 0.000 | -1.285998 | -.7145831 |
| Prairies | .2874948 | .1151471 | 2.50 | 0.013 | .0618107 | .5131789 |
| BC | -.3100151 | .1035028 | -3.00 | 0.003 | -.5128768 | -.1071534 |
| cma7 | .4066035 | .1910132 | 2.13 | 0.033 | .0322246 | .7809824 |
| bregion1 | -.2648533 | .2925672 | -0.91 | 0.365 | -.8382744 | .3085678 |
| bregion3 | .0995336 | .305917 | 0.33 | 0.745 | -.5000527 | .69912 |
| bregion4 | -.3280924 | .228842 | -1.43 | 0.152 | -.7766145 | .1204298 |
| bregion5 | -.702198 | .244845 | -2.87 | 0.004 | -1.182085 | -.2223106 |
| min1 | -.9100354 | .2500677 | -3.64 | 0.000 | -1.400159 | -.4199117 |
| min2 | .0407751 | .2390026 | 0.17 | 0.865 | -.4276613 | .5092115 |
| min3 | -.1819008 | .2183392 | -0.83 | 0.405 | -.6098377 | .2460361 |
| min4 | .6222302 | .2898216 | 2.15 | 0.032 | .0541902 | 1.19027 |
| min5 | -.5215466 | .3444505 | -1.51 | 0.130 | -1.196657 | .1535639 |
| min6 | -.2768887 | .1967725 | -1.41 | 0.159 | -.6625557 | .1087783 |
| min7 | -.8182016 | .2831731 | -2.89 | 0.004 | -1.373211 | -.2631926 |
| min8 | -.065734 | .3900471 | -0.17 | 0.866 | -.8302123 | .6987443 |
| ed1 | .1318664 | .1350965 | 0.98 | 0.329 | -.1329179 | .3966507 |
| ed2 | .1330504 | .1757951 | 0.76 | 0.449 | -.2115017 | .4776025 |
| ed3 | -.0327392 | .1278272 | -0.26 | 0.798 | -.2832758 | .2177974 |
| ed5 | -.0111976 | .0995632 | -0.11 | 0.910 | -.2063379 | .1839427 |
| insch | -1.140078 | .0864846 | -13.18 | 0.000 | -1.309585 | -.9705717 |
| Eng | .1298138 | .115577 | 1.12 | 0.261 | -.0967131 | .3563406 |
| Fre | .0156922 | .1419002 | 0.11 | 0.912 | -.2624271 | .2938114 |
| prework | .4016835 | .1404277 | 2.86 | 0.004 | .1264502 | .6769167 |
| lengthca | .1853822 | .0685596 | 2.70 | 0.007 | .0510079 | .3197565 |
| lengthsq | -.5139186 | .2567438 | -2.00 | 0.045 | -1.017127 | -.01071 |
| jobarranged | 1.743389 | .2073841 | 8.41 | 0.000 | 1.336924 | 2.149855 |
| visitbf | -.0391938 | .1179006 | -0.33 | 0.740 | -.2702747 | .191887 |
| workbf | .2173325 | .2750612 | 0.79 | 0.429 | -.3217776 | .7564426 |
| studybf | .649554 | .2066795 | 3.14 | 0.002 | .2444696 | 1.054638 |
| spwkcur | .7706661 | .1185297 | 6.50 | 0.000 | .5383523 | 1.00298 |
| spwage | -.0003937 | .0002214 | -1.78 | 0.075 | -.0008277 | .0000402 |
| relative | -.1288294 | .2097851 | -0.61 | 0.539 | -.5400005 | .2823418 |
| nr | -.0072518 | .0648803 | -0.11 | 0.911 | -.1344149 | .1199113 |
| rlnear | .275572 | .198389 | 1.39 | 0.165 | -.1132632 | .6644072 |
| fsdensity | .3784671 | .1665552 | 2.27 | 0.023 | .0520248 | .7049094 |
| friend | -.1587796 | .1272786 | -1.25 | 0.212 | -.408241 | .0906818 |
| frnear | .2339187 | .1186878 | 1.97 | 0.049 | .001295 | .4665425 |
| newfri | .1444655 | .1722342 | 0.84 | 0.402 | -.1931073 | .4820382 |
| nfoutwk | -.1062178 | .0265518 | -4.00 | 0.000 | -.1582584 | -.0541771 |
| frdiv | .3795836 | .1718096 | 2.21 | 0.027 | .0428428 | .7163243 |
| frdensity | .1736812 | .1589156 | 1.09 | 0.274 | -.1377877 | .4851501 |
| pgo | .2223838 | .2611897 | 0.85 | 0.395 | -.2895385 | .7343062 |
| ngo | .0097016 | .1699385 | 0.06 | 0.954 | -.3233718 | .3427749 |
| godiv | 1.358319 | 2.41174 | 0.56 | 0.573 | -3.368604 | 6.085243 |
| godensity | -.5040376 | .3178618 | -1.59 | 0.113 | -1.127035 | .1189601 |
| govo | -.0037153 | .1373188 | -0.03 | 0.978 | -.2728551 | .2654246 |
| _cons | -1.991571 | .6896534 | -2.89 | 0.004 | -3.343267 | -.6398755 |
| /lnsig2u | .2068822 | .1191101 | -.0265693 | .4403338 | ||
| sigma_u | 1.10898 | .0660454 | .9868032 | 1.246285 | ||
| rho | .2721057 | .0235915 | .2283914 | .3207094 | ||
Likelihood-ratio test of rho=0: chibar2(01) = 87.23 Prob >= chibar2 = 0.000
We can think of rho ( ![]() ) as being the (analogous) equivalent of the intra-cluster correlation (icc) in a multilevel model. Therefore when
) as being the (analogous) equivalent of the intra-cluster correlation (icc) in a multilevel model. Therefore when ![]() is zero the panel model is not a significant improvement on the pooled one. Here, the p value of the likelihood-ratio test of
is zero the panel model is not a significant improvement on the pooled one. Here, the p value of the likelihood-ratio test of ![]() = 0 tells us that the null hypothesis is rejected and there exists unobserved heterogeneity so that panel data model is favoured over the pooled estimator.
= 0 tells us that the null hypothesis is rejected and there exists unobserved heterogeneity so that panel data model is favoured over the pooled estimator.