How a meteorological-based tool could be used to predict West Nile virus infection

 Download this article as a PDF
Download this article as a PDF Published by: The Public Health Agency of Canada
Issue: Volume 48-5, May 2022: Vector-Borne Infections–Part 1: Ticks & Mosquitoes
Date published: May 2022
ISSN: 1481-8531
Submit a manuscript
About CCDR
Browse
Volume 48-5, May 2022: Vector-Borne Infections–Part 1: Ticks & Mosquitoes
Implementation Science
A meteorological-based forecasting model for predicting minimal infection rates in Culex pipiens-restuans complex using Québec's West Nile virus integrated surveillance system
Julie Ducrocq1, Karl Forest-Bérard1, Najwa Ouhoummane1, Elhadji Laouan Sidi1, Antoinette Ludwig2, Alejandra Irace-Cima1
Affiliations
1 Institut national de santé publique du Québec, Montréal, QC
2 Scientific Operations and Response, National Microbiology Laboratory, Public Health Agency of Canada, Saint-Hyacinthe, QC
Correspondence
Suggested citation
Ducrocq J, Forest-Bérard K, Ouhoummane N, Laouan Sidi E, Ludwig A, Irace-Cima A. A meteorological-based forecasting model for predicting minimal infection rates in Culex pipiens-restuans complex using Québec’s West Nile virus integrated surveillance system. Can Commun Dis Rep 2022;48(5):196–207. https://doi.org/10.14745/ccdr.v48i05a03
Keywords: epidemiology, outbreaks, forecasting tool, Québec, West Nile virus
Abstract
Background: The ministère de la Santé et des Services sociaux (MSSS) du Québec (Québec’s health authority) has expressed an interest in the development of an early warning tool to identify seasonal human outbreaks of West Nile virus infection in order to modulate public health interventions. The objective of this study was to determine if a user-friendly meteorological-based forecasting tool could be used to predict minimal infection rates for the Culex pipiens-restuans complex—a proxy of human risk—ahead of mosquito season.
Methods: Annual minimal infection rate (number of positive pools/number of mosquitoes) was calculated for 856 mosquito traps set from 2003 to 2006 and 2013 to 2018 throughout the south of Québec’s. Coefficient of determination (R2) were estimated using the validation dataset (one third of the database by random selection) with generalized estimation equations, which were prior fitted backwards with polynomial terms using the training dataset (two thirds of the database), in order to minimize the Bayesian information criteria. Mean temperatures and precipitation were grouped at five temporal scales (by month, by season and by 4, 6 and 10-months groupings).
Results: Mean temperatures and cumulative precipitation from the previous months of March (R2=0.37), May (R2=0.36), December (R2=0.35) and the autumn season (R2=0.38) accounted for ~40% of Cx. pipiens-restuans annual minimal infection rates variations. Including the “year of sampling” variable in all regression models increased the predictive abilities (R2 between 0.42 and 0.57).
Conclusion: All regression models explored have too weak predictive abilities to be useful as a public health tool. Other factors implicated in the epidemiology of the West Nile virus need to be incorporated in a meteorological-based early warning model for it to be useful to the provincial health authorities.
Introduction
West Nile virus (WNV) has been the most important mosquito-borne infection in Québec for the past two decadesFootnote 1. A provincial surveillance program specific for this arbovirus has been put in place since 2000Footnote 2, one year after its first detection in North America following an outbreak of neuro-invasive diseases in the state of New York, United States (US)Footnote 3. It was composed of an enhanced passive surveillance of humans, of sick or dead wild birds (which act as reservoirs or accidental hosts) and active mosquito surveillanceFootnote 4.The surveillance system confirmed WNV’s introduction in Québec in 2002 with the first WNV-positive birds and locally-acquired human casesFootnote 5Footnote 6. Neurological cases of WNV-infections typically represent a very small proportion (~1%) of infected individuals since 70% to 80% of infections remain asymptomatic, while the rest have unspecific symptoms (i.e. influenza-like illness)Footnote 3. Between 2003 and 2018, a total of 541 cases (n=24 deaths) were reported in Québec with the following clinical presentation: neurological impairment (70%); non-neurological (23%); asymptomatic (6%); and unknown (1%)Footnote 1. Since then, two peaks of reported cases have been observed in 2012 (n=134; 30% of cases from across Canada) and 2018 (n=200; 46% of cases from across Canada)Footnote 1Footnote 7.Yearly fluctuations in the number of human cases are observed in other regionsFootnote 8Footnote 9 and appeared to be associated with phenomena occurring at different geographic and temporal scalesFootnote 10 (i.e. according to local interactions between mosquitoes, birds and humans, environmental factors and large-scale climatic fluctuations such as the El Niño-Southern Oscillation)Footnote 11Footnote 12Footnote 13Footnote 14.
Scientists are still working to understand and identify factors influencing outbreaks of WNV infections, and to develop models that would be able to predict when and where these outbreaks could potentially occur. The provincial health authority (Ministère de la Santé et des Services sociaux) expressed an interest in the development of an early warning tool to identify outbreak years in advance, and to use this information to mitigate risk and decrease human exposure by modulating their interventions. Such tools are generally based on meteorological data in order to predict a potential outbreak with a delay ranging from a few weeks to a few months before the surveillance system confirms that WNV is circulatingFootnote 15. Temperature and precipitation are the most commonly used WNV predictorsFootnote 16. The main goal of this project is to determine if a meteorological-based early warning tool could predict WNV infection rates in mosquitoes.
Methods
The history of Québec’s WNV integrated (using human, animal and entomological components) surveillance system is fully described elsewhereFootnote 17. Background screening of the scientific literature was used to build a directed acyclic graph (DAG) (Figure A1) to conceptualize relationships between potential drivers of WNV and identify important variables to include in models, using the DAGitty toolFootnote 18.
Data from 13,830 mosquito pools of the Culex pipiens-restuans complex, these two species espèces (Cx. pipiens and Cx. restuans) cannot be differentiate morphologicallyFootnote 19, were extracted from the Système intégrée des données de vigie sanitaire du virus du Nil occidentalFootnote 20 to calculate annual minimal infection rate (MIR) (number of positive pools/number of mosquitoes in each pool) (Figure 1). The MIRs were calculated for each of the 856 mosquito pools, which were grouped for each trap deployed per year (i.e. mosquito trap-year) and distanced by greater or equal to 1 km2 radius, since it represents the average travel distance of Cx. pipiens-restuansFootnote 21 and the spatial resolution of the meteorological data (1 km2). Mosquito surveillance was carried out inconsistently in 12 out of 18 Public Health Units (PHU), with a greater number of mosquito pools tested for Montreal and Montérégie (Table 1), except since 2017 where 49 traps are deployed annually in the same seven PHU (Montréal=5, Laval=4, Montérégie=5, Outaouais=7, Lanaudière=7, Mauricie-Centre-du-Québec=7 et Capitale-Nationale=14).
Figure 1: Flow chart of the entomological data extracted from Québec’s Système intégrée des données de vigie sanitaire du virus du Nil occidental
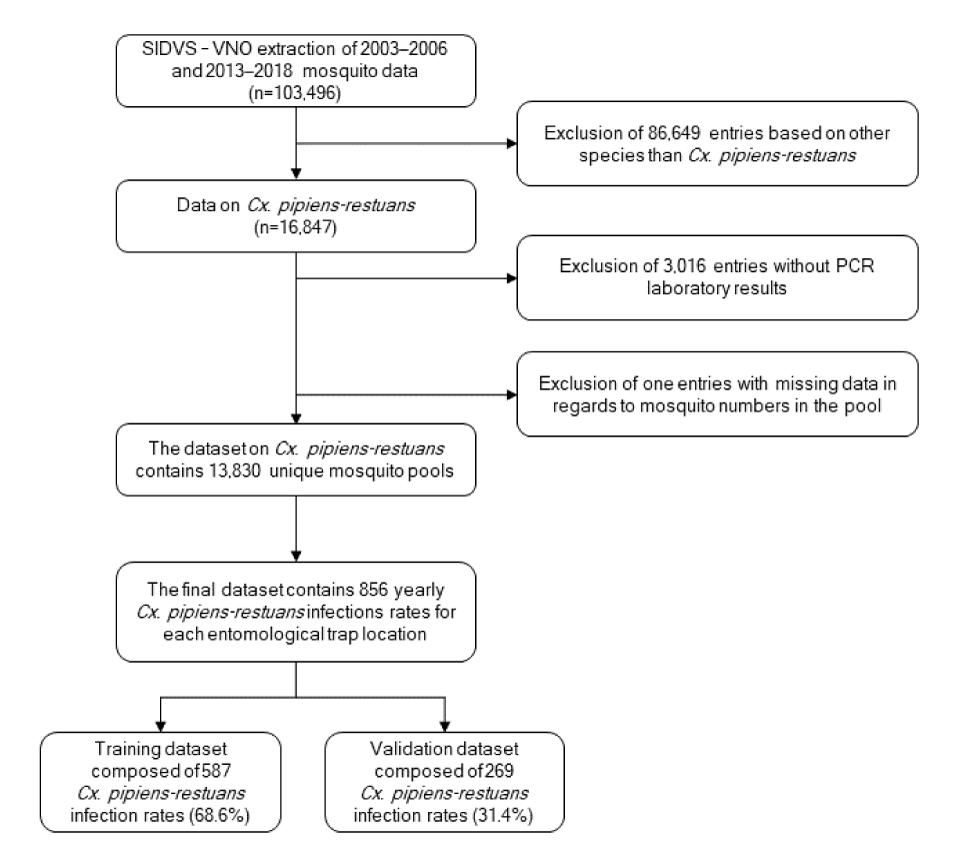
Text description: Figure 1
This figure is a flowchart explaining why some mosquito observations were excluded from the final analysis. Of the 103,496 mosquito pools found in the 2003 to 2018 data extraction, 86,649 observations were excluded because pools were composed of other mosquito species than the main vector of west Nile virus (Culex pipiens-restuans), 3,016 observations were excluded because mosquito pools were not sent to the laboratory and one observation was excluded because of missing data on the number of mosquitos in the pool. This resulted in a final dataset composed of 13,830 mosquito pools composed of the Culex pipiens-restuans complex that were regrouped into 856 minimal infection rates were representing every yearly entomological trap deployed since 2003. This dataset was then separated into a training dataset composed of 587 infection rates (2/3 of the dataset) and into a validation dataset composed of 269 infection rates (1/3 of the dataset) to assess the predictive capabilities of models.
| Spatio-temporal variables | Number of data entry | Minimal infection rate per 1,000 mosquitoes | Mean temperatures at mosquito traps | Mean precipitation at mosquito traps | |||
|---|---|---|---|---|---|---|---|
| n | 95% CI | n | min; max | n | min; max | ||
| Province of Québec | 856 | 3.1Table 1 Footnote a | 2.2; 4.0Table 1 Footnote a | 6.3 | 2.1; 8.2 | 3.0 | 2.2; 4.3 |
| Public Health Units | |||||||
| 01 – Bas Saint-Laurent | 0 | – | – | – | – | – | – |
| 02 – Saguenay – Lac Saint-Jean | 6 | 0 | 0; 45.9 | 2.5 | 2.1; 2.9 | 2.6 | 2.4; 2.8 |
| 03 – Capitale Nationale | 40 | 4.4 | 1.5; 7.3 | 5.0 | 3.5; 7.8 | 3.5 | 2.9; 4.3 |
| 04 – Mauricie et Centre-du-Québec | 28 | 1.6 | 0; 4.0 | 5.4 | 4.4; 7.2 | 3.1 | 2.3; 3.5 |
| 05 – Estrie | 8 | 0 | 0; 36.9 | 5.8 | 5.0; 7.0 | 3.5 | 3.0; 3.8 |
| 06 – Montréal | 265 | 3.1 | 2.2; 3.9 | 6.4 | 5.7; 8.2 | 3.0 | 2.4; 3.9 |
| 07 – Outaouais | 47 | 3.1 | 0; 7.3 | 6.0 | 3.5; 7.8 | 2.9 | 2.2; 3.9 |
| 08 – Abitibi-Témiscamingue | 3 | 0 | 0; 70.8 | 3.2 | 3.1; 3.3 | 2.7 | 2.7; 2.8 |
| 09 – Côte-Nord | 0 | – | – | – | – | – | – |
| 10 – Nord-du-Québec | 0 | – | – | – | – | – | – |
| 11 – Gaspésie-îles-de-la-Madeleine | 0 | – | – | – | – | – | – |
| 12 – Chaudières-Appalaches | 8 | 0 | 0; 36.9 | 4.6 | 3.7; 6.2 | 3.1 | 2.7; 3.6 |
| 13 – Laval | 82 | 4.9 | 3.1; 6.7 | 6.5 | 5.7; 8.0 | 3.0 | 2.5; 4.0 |
| 14 – Lanaudière | 36 | 3.5 | 0.6; 6.5 | 6.7 | 5.4; 7.8 | 3.1 | 2.3; 4.0 |
| 15 – Laurentides | 70 | 4.8 | 2.0; 7.7 | 6.4 | 5.3; 8.0 | 3.2 | 2.6; 4.2 |
| 16 – Montérégie | 263 | 3.9 | 2.9; 5.0 | 6.5 | 5.3; 8.1 | 2.9 | 2.4; 3.9 |
| 17 – Nunavik | 0 | – | – | – | – | – | – |
| 18 – Terres-Cries-de-la-Baie-James | 0 | – | – | – | – | – | – |
| Type 3 global analysis: Chi-square (p-value)Table 1 Footnote b | – | 9.9 | 0.5 | 23.3 | 0.02 | 17.2 | 0.1 |
| Year | |||||||
| 2003 | 118 | 3.0 | 1.7; 4.4 | 5.5 | 3.1; 6.3 | 2.6 | 2.3; 3.4 |
| 2004 | 86 | 0.9 | 0; 2.1 | 5.7 | 2.1; 6.5 | 3.1 | 2.4; 3.8 |
| 2005 | 146 | 3.4 | 2.0; 4.8 | 6.5 | 3.7; 7.0 | 3.1 | 2.4; 4.3 |
| 2006 | 65 | 0.2 | 0; 0.4 | 7.5 | 6.8; 7.9 | 3.8 | 3.1; 4.2 |
| 2007 | 0 | – | – | – | – | – | – |
| 2008 | 0 | – | – | – | – | – | – |
| 2009 | 0 | – | – | – | – | – | – |
| 2010 | 0 | – | – | – | – | – | – |
| 2011 | 0 | – | – | – | – | – | – |
| 2012 | 0 | – | – | – | – | – | – |
| 2013 | 63 | 5.5 | 3.2; 7.8 | 7.1 | 6.4; 7.5 | 2.8 | 2.4; 3.1 |
| 2014 | 199 | 4.2 | 2.7; 5.6 | 6.0 | 5.7; 6.2 | 3.0 | 2.8; 3.2 |
| 2015 | 45 | 5.6 | 2.6; 8.7 | 6.2 | 4.5; 6.5 | 2.7 | 2.2; 3.4 |
| 2016 | 47Table 1 Footnote c | 5.6 | 2.3; 9.0 | 7.0 | 3.1; 8.2 | 3.0 | 2.5; 3.8 |
| 2017 | 46Table 1 Footnote c | 5.4 | 3.2; 7.7 | 6.5 | 5.1; 7.7 | 3.5 | 3.2; 3.9 |
| 2018 | 41Table 1 Footnote c | 11.8 | 0; 91.1 | 6.2 | 4.7; 7.5 | 3.1 | 2.6; 3.5 |
| Type 3 global analysis: Chi-square (p-value)Table 1 Footnote b | – | 28.5 | 0.008 | 61.1 | <0.0001 | 53.9 | <0.0001 |
| MonthTable 1 Footnote d | |||||||
| January | 0 | – | – | -10.8 | −19.7; −4.2 | 2.0 | 0.6; 5.3 |
| February | 0 | – | – | -8.8 | −16.9; −4.1 | 2.1 | 0.9; 5.4 |
| March | 0 | – | – | -3.8 | −7.3; 0.5 | 2.0 | 0.8; 5.0 |
| April | 0 | – | – | 5.4 | −3.0; 7.8 | 3.6 | 0.2; 7.4 |
| May | 96 | 0 | 0; 37.7 | 13.4 | 7.5; 16.6 | 3.2 | 0.7; 6.8 |
| June | 1,518 | 0 | 0; 0.1 | 18.7 | 13.1; 21.4 | 4.2 | 1.5; 7.6 |
| July | 3,611 | 0.8 | 0.4; 1.2 | 21.1 | 18.0; 23.5 | 3.2 | 1.6; 7.2 |
| August | 4,688 | 5.5 | 4.3; 6.7 | 20.1 | 16.4; 22.3 | 3.5 | 1.7; 6.2 |
| September | 3,675 | 6.0 | 4.4; 7.5 | 16.1 | 12.4; 18.6 | 2.9 | 0.8; 7.7 |
| October | 242 | 1.9 | 0; 4.4 | 9.0 | 3,4; 12.9 | 3.4 | 1.2; 6.8 |
| November | 0 | – | – | 1.4 | −2.3; 4.4 | 3.0 | 0.3; 5.6 |
| December | 0 | – | – | −6.5 | −11.8; 1.8 | 3.2 | 0.6; 7.1 |
| Type 3 global analysis: Chi-square (p-value)Table 1 Footnote b | – | 15.6 | <0.0001 | N/ATable 1 Footnote e | N/ATable 1 Footnote e | N/ATable 1 Footnote e | N/ATable 1 Footnote e |
Explanatory variables included the mean daily temperatures (Tmean=Tmaximal+Tminimal/2) (°C) and daily precipitation (mm) extracted from the Oak Ridge National Laboratory Distributed Active Archive Center (https://daymet.ornl.gov) according to the Global Positioning System (GPS) coordinates of each trap-year (latitude and longitude). Mean daily temperature and sum of precipitation were grouped according to five different temporal scales: 1) previous months; 2) previous seasons: summer (June and July), spring (March to May), winter (December to February) and autumn (September to November); 3) previous four-months (November of the year before to February of the same year); 4) previous six-months (September of the year before to February of the same year); and 5) previous ten-months (September of the previous year to July of the current year) groupings, based on the literature suggesting that meteorological conditions impact WNV transmission months aheadFootnote 11Footnote 22. Meteorological data from the closest neighboring traps were assigned to eight mosquito traps with missing data, with half of these traps being separated by more than one kilometer from their matched trap. To consider variations in the geographical and temporal mosquito sampling, two new “sampling strengths” variables were created for each PHU (Figure 2) based on the number of tested mosquito pool: 1) annually; and 2) during the 2003–2018 period (Table 1).
Figure 2: Map of the 18 Public Health Units in the province of Québec according to the number of mosquito pools tested between 2003–2006 and 2013–2018
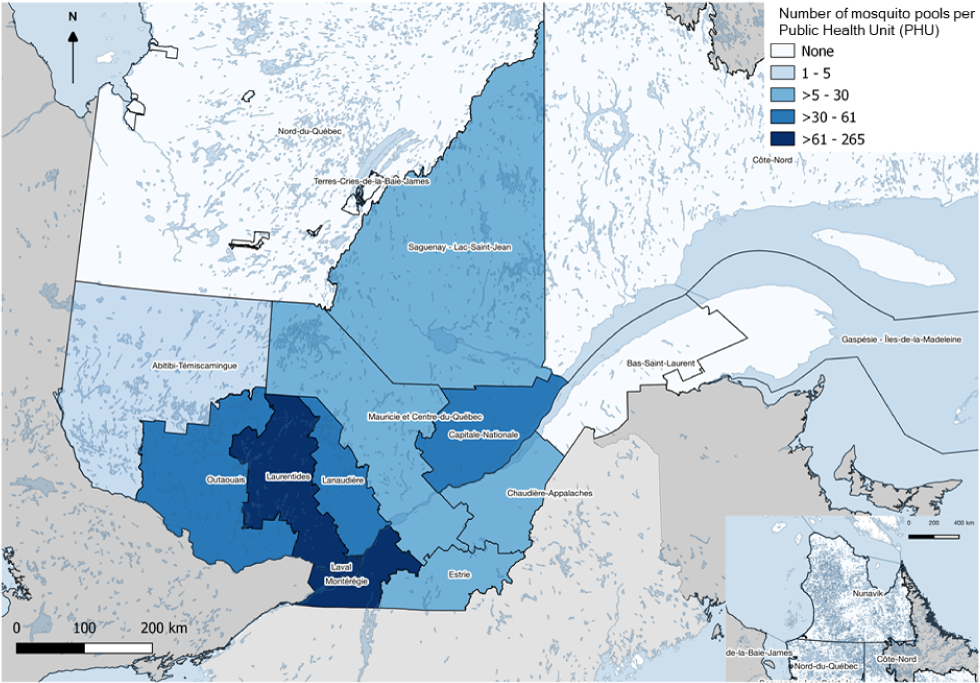
Text description: Figure 2
This is a map of Québec's 18 public health units that are colored according to the number of mosquitos' pools, to show the geographical sampling biases. Amongst the dataset composed 856 infections rates, four public health units (Montréal, Laval, Laurentides and Montérégie) have between 62 and 265 observations. The public health units of Outaouais, Lanaudière and Capitale-Nationale have between 31 and 61 observations; Estrie, Mauricie-Centre-du-Québec, Chaudières-Appalaches and Saguenay-Lac-St-Jean have between 6 and 30 observations; Abitibi-Témiscamingue have between 1 and 5 observations while, no mosquito surveillance occurred in Bas Saint-Laurent, Gaspésie-Iles-de-la-Madeleine, Côte-Nord, Nord-du-Québec, Nunavik and Terres-Cries-de-la-Baie-James.
Bivariate analysis between Cx. pipiens-restuans annual MIR (outcome) and explanatory variables (PHU, year and month) were performed using a linear regression model; an auto-regressive working covariance matrix with mosquito traps in the same city were nested within each PHU. Then multivariate regression models evaluated the predictive ability of each temperature and precipitation temporal scale to estimate MIRs, with observations randomly separated into training (n=2/3) and validation (n=1/3) datasets. A backward variable selection with a maximum of four polynomial terms to obtain the lowest Bayesian information criteria using the training dataset was fitted back into a Poisson regression model using the validation datasetFootnote 23. MIRs were obtained using the number of positive Cx. pipiens-restuans pools on the logarithm of the number of mosquitoes tested, while mosquito traps in the same city were nested within each PHU to account for correlated data using an auto-regressive working covariance matrix. The methodology of sensitivity and post hoc analyses are described in the Annex material. The SAS macro (%RsquareV) was used to calculate the coefficient of determination (R2), reflecting the proportion of the variance explained by the predictorsFootnote 24. Only R2≥0.30 are highlighted in the text. The 95% confidence intervals (CI) and p-values are presented, and all postulates associated with the regression models were visually inspectedFootnote 25. Statistical analysis were performed using version 9.4 of SAS/STATTM software (SAS Institute, Cary, North Carolina, US).
Results
Since 2003, 172,094 Cx. pipiens-restuans mosquitoes were analyzed by polymerase chain reaction (PCR), resulting in a mean MIR of 3.1 per 1,000 mosquitoes (95% CI; 2.2–4.0), when data were grouped under the 856 mosquito trap-years, which varied according to the sampling year (χ2=28.5; p=0.0008) and month (χ2=15.6; p<0.0001) but not across the PHU (χ2=9.9; p=0.5) (Table 1). For the studied period, mean monthly temperatures near mosquito traps varied from 23.5°C (July) to −19.7°C (January) while monthly cumulative precipitation varied from 0.3 mm (November) to 7.7 mm (September).
The predictive ability of the previous mean temperatures and precipitation to predict the seasonal MIRs was the highest using the previous months of March (R2=0.37), May (R2=0.36) and December (R2=0.35) as well as the previous autumn season (R2=0.38), with all other coefficients of determination below 0.30 (Table 2). The results of all the sensitivity and post hoc analysis are fully described in the Annex material. Briefly, including the year of sampling variable in the main regression models increased all R2 (range: 0.42 to 0.57) while the increased was less substantial when including the PHU variable (range: 0.18 to 0.46) (Table A1).
| Regression models and equations from the training dataset | Coefficient of determination of the validation dataset (Penalised R2) |
|
|---|---|---|
| A) By previous month | ||
| July | MIR = -915.67 + 130.81Temp - 6.45Temp2 + 0.11Temp3 + 35.05Prec – 14.65Prec2 + 2.58Prec3 – 0.17Prec4 + ε | 0.28 |
| JuneTable 2 Footnote a | MIR = -40.79 + 3.54Temp – 0.10Temp2 + 0.95Prec – 0.09Prec2 + ε | 0.15 |
| MayTable 2 Footnote a | MIR = 13.60 – 2.13Temp + 0.09Temp2 – 7.98Prec + 2.48Prec2 – 0.24Prec3 + ε | 0.36 |
| April | MIR = -7.64 – 0.27Temp + 2.47Prec – 0.69Prec2 + 0.08Prec3 – 0.003Prec4 + ε | 0.19 |
| March | MIR = -22.03 – 4.28Temp – 2.31Temp2 - 0.44Temp3 – 0.03Temp4 + 30.83Prec – 22.71Prec2 + 6.79Prec3 – 0.70Prec4 + ε | 0.37 |
| February | MIR = -2.85 + 2.38Temp + 0.20Temp2 – 0.01Temp3 + ε | 0.10 |
| January | MIR = -47.75 – 17.42Temp – 2.65Temp2 - 0.18Temp3 – 0.004Temp4 + 0.34Prec – 0.04Prec2 + ε | 0.24 |
| December | MIR = -6.93 + 0.21Temp – 0.05Temp2 – 0.01Temp3 + 2.67Prec – 0.79Prec2 – 0.06Prec3 + ε | 0.35 |
| November | MIR = -4.74 – 0.07Temp – 0.46Temp2 + 0.12Temp3 + 2.61Prec + 2.74Prec2 – 0.65Prec3 + 0.09Prec4 + ε | 0.18 |
| October | MIR = -7.48 + 0.20Temp – 0.83Prec + 0.47Prec2 + 0.06Prec3 + ε | 0.28 |
| September | MIR = -6.02 + 0.16Temp – 1.75Prec + 0.26Prec2 + ε | 0.28 |
| August | MIR = -13.09 + 0.40Temp – 0.24Prec + ε | 0.08 |
| B) By seasonTable 2 Footnote b | ||
| SummerTable 2 Footnote a | MIR = -45.53 + 4.37Temp – 0.11Temp2 – 3.25Prec + 0.46Prec2 + ε | 0.15 |
| SpringTable 2 Footnote c | MIR = -206.81 + 84.33Temp – 25.56Temp2 + 3.36Temp3 – 0.16Temp4 + 132.67Prec – 64.01Prec2 + 13.26Prec3 – 1.00Prec4 + ε | 0.09 |
| Winter | MIR = 2.31 + 0.89Temp + 0.05Temp2 – 6.40Prec + 3.04Prec2 – 0.46Prec3 + ε | 0.24 |
| Autumn | MIR = -438.86 + 153.19Temp – 17.32Temp2 + 0.65Temp3 – 15.35Prec + 4.79Prec2 – 0.50Prec3 + ε | 0.38 |
| C) From November of the previous year to February of the same year | ||
| Four months grouped together | MIR = -48.07 – 2.87Temp – 1.24Temp2 – 0.18Temp3 – 0.01Temp4 + 54.97Prec – 26.15Prec2 + 15.35Prec3 – 0.41Prec4 + ε | 0.24 |
| D) From September of the previous year to February of the same year | ||
| Six months grouped together | MIR = 9.37 + 0.48Temp – 0.23Prec + 13.46Prec2 – 3.51Prec3 + 0.33Prec4 + ε | 0.27 |
| E) From September of the previous year to July of the same yearTable 2 Footnote c | ||
| Ten months grouped together | MIR = -119.02 – 113.69Temp – 41.82Temp2 + 6.68Temp3 – 0.39Temp4 + ε | 0.12 |
Discussion
This is the first time that a meteorological-based early warning tool to predict Cx. pipiens-restuans annual MIRs in Québec has been investigated using the province’s own WNV surveillance data. The ability of mean temperatures and precipitation to predict MIRs was highest when the data were grouped under the previous months of March, December and May, and previous autumn season (September to November of the previous year). However, the predictive capacity of the model is probably too weak to be useful for an early warning system. The fact that only ~40% of the variance in Cx. pipiens-restuans annual MIRs can be explained by mean temperature and precipitation suggests that others factors are implicated in the epidemiology of WNV and that these factors need to be incorporated into this kind of predictive toolFootnote 15.
Many early warning or forecasting systems that are primarily or solely based on meteorological data have been developed to predict other mosquito-borne diseases (i.e. chikungunya, dengue, malaria, yellow fever, Zika) to anticipate vector control responsesFootnote 24. Our results suggest that presently these models yield insufficient predicting abilities to be useful in real life for Quebec’s public health authority. The epidemiology of WNV is known to be complex and adding variables such as environmental drivers (habitat suitability or distribution of vectors and reservoirs, vegetation index, land use) and data on avian hosts (abundance, migrations) usually improve predictionsFootnote 15. However, the necessity of integrating data from the ongoing surveillance system and refining the geographical scale leads to less user-friendly tools, for public health authoritiesFootnote 26.
Strengths and limitations
One of the strengths of this project is that the geographical proximity of mosquito traps was accounted for in most of the regression models, as this can bias results. Additionally, multiple sensitivity and post hoc analyses brought robustness to our results. The polynomial equations accounted for non-linear associations between meteorological variables and MIRs, allowing for a better representation of their relationship and a better model fit, while the backward selection of variables proved to be as effective as the visual inspection of generalized additive models. Because MIRs are low numerical values, an attempt to increase the statistical power was made by calculating annual MIRs using mosquitoes trapped during August and September. Though the mean annual MIRs increased for most positive mosquito pools, the coefficient of determination for most regression models decreased unexpectedly; possibly as a consequence of a smaller sample size when including only August and September, since 13 mosquito traps had no mosquitoes captured, which decreased statistical power.
Based on our conceptual framework, it is unknown if an over adjustment bias occurred when adjusting for “year of sampling” in the regression modelsFootnote 27. Despite multiple sensitivity analysis with potential confounding variables, a residual confounding effect cannot be discardedFootnote 28. Because mosquito pools were grouped for each trap-year, it was not possible to account for the different types of traps that were employed. This limitation has probably a marginal effect, since 85.2% of mosquitoes were captured by the CDC light traps. It was not possible to account for the use of larvicides during the 2003–2005 and 2013–2014 seasons, which might have influenced the estimates. Because mosquito PCR testing is done independently from mosquito trapping, if a measurement bias was to be present, a decrease in the association would also be suspected.
A selection bias could influence our results because of the geographical distribution of traps which is linked to 1) past human WNV incidence and 2) the influence of weather on human physical activity and exposure to mosquitoesFootnote 29Footnote 30. Additionally, the fixed location of mosquitoes traps since 2017 comes at the expense of detecting WNV emergence in the less densely populated PHU situated at more northern latitudes. The limited number of mosquito traps on such a huge territory and the absence of mosquito surveillance during the colder months reduces the statistical power. Hence, a higher number of traps distributed over a wider geographical area would provide a wider range of meteorological data and increase statistical power. Since WNV vectors vary according to regions, and transmission pathways seem to be influenced environmental and geographical variables at a finer scale then the PHU results of this project may not be transferable to other situations. Despite these limitations, Québec’s WNV surveillance data will be explored further. The next steps will be to directly predict human WNV incidence using meteorological data and bypass the gap that occurred in entomological data between 2007 and 2012 and to explore the development of an early detection system tool.
Conclusion
All regression models explored have too weak predictive abilities to be useful as a public health tool. Other factors implicated in the epidemiology of the West Nile virus need to be incorporated in a meteorological-based early warning model for it to be useful to the provincial health authorities.
Authors’ statement
KFB, NO, AL and AIC — Conceptualized the project
ESL — Performed database management and statistical analysis
JD — Conceptualized the project, performed database management and statistical analysis, interpretation of results, wrote original draft
All coauthors reviewed and edited the text.
Competing interests
None.
Acknowledgements
We would like to acknowledge the Ministère de la Santé et des Services who funds the integrated West Nile virus surveillance program since 2003, which encompasses annual mosquito sampling by a private company, PCR testing on mosquitoes done by the Laboratoire de santé publique du Québec (LSPQ) as well as data hosting, management and analysis through the Institut national de santé publique du Québec (INSPQ).
Funding
This project was funded by the Public Health Agency of Canada through the “Protocole d’accord relatif à la recherche sur les risques d’émergence de maladies à transmission vectorielle en raison des changements climatiques 2020-2022” concluded with the Institut national de santé publique du Québec (INSPQ).
Annex
Methods
Because human cases of West Nile virus (WNV) infection are usually reported at the beginning of AugustFootnote 1 and that the objective is to develop an early alert tool able to predict these human cases a couple of months before they occur, temperatures and precipitation during August have not been included in our analysis.
Background screening of the scientific literature was used to build a directed acyclic graph (DAG) (Figure A1) to conceptualize relationships between potential drivers of WNV and identify the variables that need to be adjusted for in the model using the DAGitty tool.
Figure A1: Conceptual framework using a directed acyclic graph between meteorological variables and the main outcomes of Québec's West Nile virus integrated surveillance system
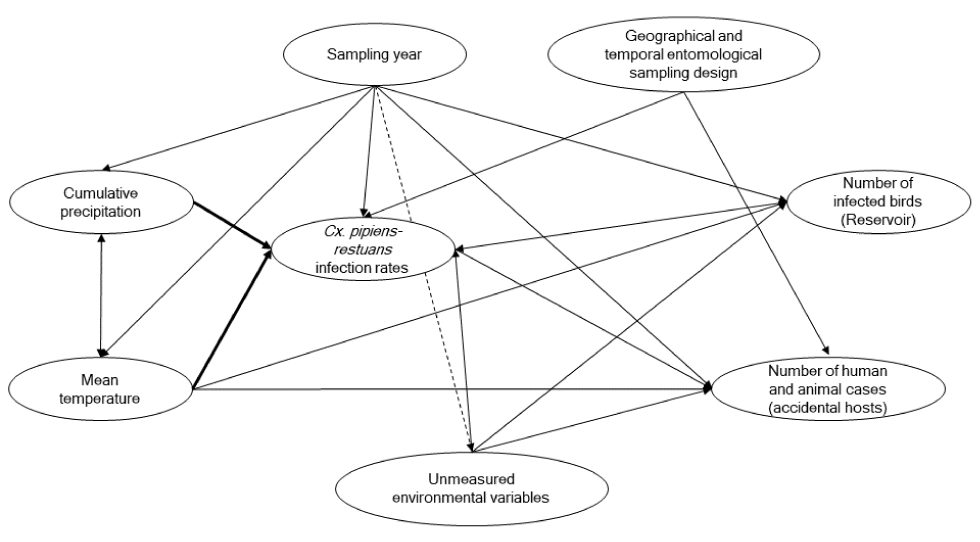
Text description: Figure A1
This figure is a directed acyclic graph (or DAG) showing the different relationships between the mean daily temperatures and cumulative precipitations, which are the explanatory variables and the outcome, which is Culex pipiens-restuans minimal infection rates. Based on the scientific literature, It represent the conceptual framework that helps guide the statistical analysis, as it allows to identify all other variables to include in the models. The other variables that are included in the graph are the sampling year, the number of infected birds (as reservoir of the virus), the number of human and animal cases (as accidental hosts), the geographical and temporal entomological sampling design and unmeasured environmental variables.
Sensitivity and post hoc analysis
Seven sensitivity analyses were carried out as follows: 1) regression models were fitted using visual inspection of graphs generated by a generalized additive model with a maximum of four degree of smoothing performed by generalized cross validation; 2) the main models were reanalyzed without the data from the four mosquito traps (LAV 034, LAV 904, SHA 002 and WEN 001) that inherited meteorological data of their closest neighbour with a radius superior to 1 km2; 3) by including the Public Health Units (PHU) 2003–2018 sampling strength variable; 4) by including the annual sampling strength by PHU; 5) by attributing the minimal infection rate of mosquitoes trapped only during the month of August and September instead of during the whole summer; 6) by adding the year of sampling in the model; and 7) by adding the PHU in the model instead of in the repeated measure. Following results from the 6th sensitivity analysis, year of sampling was used as a proxy for unmeasured confounders. An post hoc Poisson analyses was performed by modeling directly the MIR using the year of sampling (categorical) as the explanatory variable. To measure if the meteorological variables were confounders of this association, the year of sampling was included as a continuous variable to facilitate the calculation and interpretation of the difference and ratio between both estimates (βYear of sampling). Confounding was present based on a difference and/or ratio of estimates superior to 0.1 decimal or 10%Footnote 31. Four additional bivariate analysis were carried out with the year of sampling as an explanatory continuous variable and respectively, the mean annual temperatures, mean annual precipitation, annual sampling strength and PHU sampling strength as the main outcome. Specifying a normal distribution, an “identity” link and an auto-regressive working covariance matrix with mosquito traps in the same city nested within each PHU, yielded estimates representing differences in minimal infection rates (MIRs).
Results
Sensitivity analysis
Fitting regression models after a visual inspection of the generalized additive model graphs led to similar results of the main analysis, except for the month of February (R2 increased to 0.22) and August (R2 increased to 0.24) as well as the ten-month grouped (R2 increased to 0.18), while all other comparisons had difference within five decimal units (Table A1). Excluding the four entomological traps with meteorological data borrowed from the closest neighboring trap influenced the results for the months of May (R2 decreased to 0.19) and September (R2 increased to 0.38), summer (R2 increased to 0.29) and winter (R2 decreased to 0.16) (Table A1). When including the PHU sampling strength variable, all R2 were within five decimals of the main results (Table A1). Including the variable reflecting the annual strength of sampling, increased the predictive abilities of at least five decimals for nine temporal groupings (June, April, February, November, August; summer and spring; the six and ten-months groupings). Using the minimal infection rates of Cx. pipiens-restuans trapped in August and September instead of the whole summer, influenced the R2 for 14 temporal groupings (decreased for May, April, December, November, September, summer, winter, autumn, four and six-months grouping and increased for June, October, August and spring). When including the year of sampling in the main regression models, all coefficient of determination increased between 0.42 and 0.57. Including the PHU variable in the main regression models increased the predictive ability of at least five decimals for all temporal groupings except July, May and autumn.
| Regression models | Sensitivity analysesTable A1 Footnote a | ||||||
|---|---|---|---|---|---|---|---|
| Using generalized additive models for model specifications | Without the four entomological traps | Including the PHU strength of sampling variable | Including the annual sampling strength variable | Using the August and September MIR | Adding the year of sampling in the main model | Adding the PHU variable in the main model | |
| A) By previous month | |||||||
| July | 0.28 | 0.28 | 0.27 | 0.30 | 0.31 | 0.56↑ | 0.29 |
| JuneTable A1 Footnote b | 0.18 | 0.15 | 0.17 | 0.21↑ | 0.24↑ | 0.53↑ | 0.24↑ |
| MayTable A1 Footnote b | 0.36 | 0.19↓ | 0.35 | 0.39 | 0.30↓ | 0.53↑ | 0.35 |
| April | 0.23 | 0.19 | 0.19 | 0.31↑ | 0.13↓ | 0.55↑ | 0.31↑ |
| March | 0.37 | 0.37 | 0.38 | 0.34 | 0.41 | 0.53↑ | 0.46↑ |
| February | 0.22↑ | 0.22↑ | 0.10 | 0.20↑ | 0.09 | 0.53↑ | 0.22↑ |
| January | 0.26 | 0.24 | 0.24 | 0.27 | 0.21 | 0.57↑ | 0.30↑ |
| December | 0.33 | 0.34 | 0.37 | 0.36 | 0.29↓ | 0.53↑ | 0.41↑ |
| November | 0.18 | 0.18 | 0.19 | 0.33↑ | 0.04↓ | 0.54↑ | 0.36↑ |
| October | 0.28 | 0.28 | 0.27 | 0.30 | 0.34↑ | 0.51↑ | 0.41↑ |
| SeptemberTable A1 Footnote b | 0.29 | 0.38↑ | 0.30 | 0.35↑ | 0.21↓ | 0.57↑ | 0.38↑ |
| August | 0.24↑ | 0.11 | 0.09 | 0.23↑ | 0.24↑ | 0.48↑ | 0.20↑ |
| B) By seasonTable A1 Footnote c | |||||||
| Summer | 0.14 | 0.29↑ | 0.15 | 0.24Table A1 Footnote d↑ | 0.02↓ | 0.55↑ | 0.27Table A1 Footnote e↑ |
| Spring | 0.09 | 0.09 | 0.09 | 0.18↑ | 0.15Table A1 Footnote e↑ | 0.53↑ | 0.23Table A1 Footnote e↑ |
| Winter | 0.20 | 0.16↓ | 0.23 | 0.26 | 0.08↓ | 0.51↑ | 0.32↑ |
| Autumn | 0.38 | 0.38 | 0.38 | 0.40 | 0.27↓ | 0.53↑ | 0.41 |
| C) Four months grouping | |||||||
| From November of the year before to February of the same year | 0.26 | 0.24 | 0.24 | 0.23 | 0.14↓ | 0.57↑ | 0.35↑ |
| D) Six months grouping | |||||||
| From September of the year before to February of the same year | 0.27 | 0.26 | 0.29 | 0.34↑ | 0.19↓ | 0.56↑ | 0.36↑ |
| E) Ten months grouped togetherTable A1 Footnote bTable A1 Footnote d | |||||||
| From September of the year before to July of the same year | 0.18↑ | 0.12Table A1 Footnote e | 0.13Table A1 Footnote e | 0.20↑ | 0.17 | 0.42↑ | 0.18↑ |
Post hoc analysis
When modelling directly the MIR using only the “year of sampling” variable, the R2 was 0.53. The estimate associated with the year of sampling on a continuous linear scale and as the only explanatory variable of Cx. pipiens-restuans MIRs was 1.09 (95% CI; 1.06–1.11; p<0.0001) while yearly fluctuations are observed when treated on the categorical scale (results not shown). The results of the estimates obtained in all the main regression models using the meteorological variables and year of sampling varied between 1.06 and 1.15, with very low confounding effects on the difference and ratio scales (Table A2). When comparing MIRs between years and using 2018 as the reference, all anterior sampling years had lower values except for 2016 since the upper 95% CI of the estimate overlaps the null value (Table A3). When the year of sampling is treated on a continuous scale, the number of mosquito traps decreased linearly from 2003 to 2018 (β=−1.13 [−1.45–−0.81; p<0.0001]). Therefore, the number of mosquito traps and MIRs are inversely correlated between 2003 and 2018 with an increase of 2% in MIRs for each less mosquito trap in time (β=0.98 [0.98–0.99; p<0.0001]). At the level of each mosquito trap location in Québec, mean annual temperatures increased (β=0.04 [0.02–0.06; p=0.0003]) while mean annual precipitation decreased (β=−0.008 [−0.02–0.006; p=0.07]) from 2003 to 2018.
| Regression models | Estimate for the sampling year as a continuous variable with meteorological data | p-value | Difference in estimatesTable A2 Footnote a | Ratio in estimates for the sampling yearTable A2 Footnote b | |
|---|---|---|---|---|---|
| n | 95% CI | ||||
| A) By previous month | |||||
| July | 1.08 | 1.04–1.12 | <0.0001 | 0.01 | 1.01 |
| JuneTable A2 Footnote c | 1.11 | 1.07–1.15 | <0.0001 | −0.02 | 0.98 |
| MayTable A2 Footnote c | 1.09 | 1.06–1.12 | <0.0001 | 0.00 | 1.00 |
| April | 1.07 | 1.04–1.11 | 0.0001 | 0.02 | 1.02 |
| March | 1.15 | 1.12–1.18 | <0.0001 | −0.06 | 0.95 |
| February | 1.08 | 1.05–1.11 | <0.0001 | 0.01 | 1.01 |
| January | 1.14 | 1.10–1.18 | <0.0001 | −0.05 | 0.96 |
| December | 1.11 | 1.06–1.14 | 0.0007 | −0.02 | 0.98 |
| November | 1.06 | 1.03–1.09 | 0.0003 | 0.03 | 1.03 |
| October | 1.08 | 1.04–1.13 | <0.0001 | 0.01 | 1.01 |
| September | 1.09 | 1.06–1.13 | <0.0001 | 0.00 | 1.00 |
| August | 1.09 | 1.07–1.12 | <0.0001 | 0.00 | 1.00 |
| B) By seasonTable A2 Footnote d | |||||
| SummerTable A2 Footnote c | 1.12 | 1.10–1.15 | <0.0001 | −0.03 | 0.97 |
| SpringTable A2 Footnote e | 1.09 | 1.06–1.1 | <0.0001 | 0.00 | 1.00 |
| Winter | 1.12 | 1.07–1.16 | <0.0001 | −0.03 | 0.97 |
| Autumn | 1.08 | 1.05–1.11 | <0.0001 | 0.01 | 1.01 |
| C) Four months grouping | |||||
| From November of the year before to February of the same year | 1.09 | 1.05–1.13 | <0.0001 | 0.00 | 1.00 |
| D) Six months grouping | |||||
| From September of the year before to February of the same year | 1.09 | 1.06–1.11 | <0.0001 | 0.00 | 1.00 |
| E) Ten months groupingTable A2 Footnote f | |||||
| From September of the year before to July of the same year | 1.08 | 1.06–1.10 | <0.0001 | 0.01 | 1.01 |
| Year of sampling | Cx. pipiens-restuans minimal infection rates per 1,000 mosquitoes | Minimal infection rate ratio | p–value | ||
|---|---|---|---|---|---|
| n | Rate | n | Rate | ||
| 2003 | 3.0 | 1.7–4.4 | 0.24 | 0.16–0.34 | <0.0001Table A3 Footnote a |
| 2004 | 0.9 | 0–2.1 | 0.06 | 0.04–0.10 | <0.0001Table A3 Footnote a |
| 2005 | 3.4 | 2.0–4.8 | 0.21 | 0.12–0.36 | <0.0001Table A3 Footnote a |
| 2006 | 0.2 | 0–0.4 | 0.05 | 0.03–0.10 | <0.0001Table A3 Footnote a |
| 2013 | 5.5 | 3.2–7.8 | 0.41 | 0.26–0.66 | 0.0002Table A3 Footnote a |
| 2014 | 4.2 | 2.7–5.6 | 0.31 | 0.20–0.46 | <0.0001Table A3 Footnote a |
| 2015 | 5.6 | 2.6–8.7 | 0.36 | 0.21–0.65 | 0.0005Table A3 Footnote a |
| 2016 | 5.6 | 2.3–9.0 | 0.50 | 0.22–1.13 | 0.1 |
| 2017 | 5.4 | 3.2–7.7 | 0.53 | 0.35–0.80 | 0.002Table A3 Footnote a |
| 2018 (Reference) | 11.8 | 0–91.1 | 1.00 | 1.00 | – |
| Type 3 global analysis (with 9 degree of liberty) | – | – | Χ2=17.98 | Χ2=17.98 | 0.04 |
