ARCHIVÉ – Capital social et entrée sur le marché du travail des nouveaux immigrants au Canada

5. Cadre des modèles

5.1 Modèles théoriques

L’importance des réseaux sociaux sur le marché du travail repose sur une variété d’explications théoriques. Celles-ci vont de l’appariement (Montgomery, 1991) ⁵ à la répartition inégale de l’information (Boorman, 1975). J’emprunte, en guise de théorie de base, un modèle de réseau simple mis au point par Calvó-Armengol et Jackson (2004). Les auteurs montrent que, dans un contexte de répartition inégale de l’information, le capital social, grâce à la transmission de l’information au sein des réseaux sociaux, atténue les frictions en matière d’appariement, influe sur le processus d’appariement emploi-travailleur, et présente une corrélation positive avec la situation d’emploi dans le temps et selon les membres du réseau. Le modèle s’articule selon la structure élémentaire suivante :

N agents vivent et travaillent durant des périodes distinctes indexées en t. Au terme d’une période t, si un agent i détient un emploi, alors s_it = 1, et s_it = 0 s’il n’en occupe pas. Une période commence lorsque certains agents occupent un emploi et d’autres non. Au cours de chaque période, un agent en particulier entend parler d’une possibilité d’emploi selon une probabilité asituée entre 0 et 1. Il est présumé que le processus d’arrivée de l’information sur l’emploi ne dépend pas des agents. L’agent qui n’a pas d’emploi prendra la place offerte. L’agent qui occupe déjà un emploi transmettra l’information de façon aléatoire à un proche, un ami ou une connaissance sans emploi. L’information ne circule qu’entre des agents qui se connaissent. Si toutes les connaissances de l’agent occupent déjà un emploi, l’information ne servira pas. Pendant ce temps, certains agents perdent leur emploi au cours d’une période donnée avec une probabilité de rupture exogène b. Alors, la probabilité qu’un agent i entende parler d’un emploi et que cet emploi échoie à l’agent j est alors p_ij (s), où s est la situation d’emploi de tous les agents au début de la période :

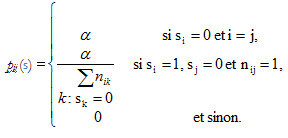
où n_ij = 1 quand les individus i et j se connaissent, ou 0 quand ils ne se connaissent pas.
Dans ce modèle, la situation d’emploi change selon les situations d’emploi précédentes et le réseau de la personne. Le modèle fournit un outil pour analyser les effets des réseaux sociaux sur les dynamiques d’emploi. Calvó-Armengol et Jackson ont utilisé ce modèle pour fournir des explications clés sur le lien entre l’emploi et la structure du réseau (sa taille et sa diversité)⁶. Bien qu’on observe à court terme une corrélation négative conditionnelle entre la situation d’emploi et la taille du réseau, cette corrélation devient positive à long terme. Le nombre d’emplois obtenus augmente avec la diversité du réseau. Des grappes équilibrées se forment dans la mesure où les travailleurs dépourvus d’un bon réseau présentent un taux de chômage plus élevé que ceux qui jouissent de réseaux de meilleure qualité. Les chercheurs ont également appliqué les résultats de ce modèle à la dynamique du salaire (Calvó-Armengol et Jackson, 2003). La présente étude rend compte d’un test empirique, réalisé dans le contexte de l’immigration, des résultats qu’implique ce modèle de réseau, et plus particulièrement de l’affirmation selon laquelle la structure du réseau est importante.

Le présent document met l’accent sur les preuves empiriques de l’effet du capital social sur la probabilité, pour les immigrants, de trouver du travail; le lien entre le capital social et le revenu fera l’objet d’une autre étude.

5.2 Méthode d’estimation et spécification du modèle

L’équation élémentaire d’estimation utilisée pour cette recherche est une régression logit de la probabilité de trouver du travail. On peut concevoir la probabilité, pour un immigrant, de trouver du travail comme une variable latente non observée y* selon laquelle 

Les modèles estimés sont de forme réduite. Les modèles structurels de disponibilité de la main-d’œuvre et de demande de travailleurs ne font pas l’objet d’estimation. L’analyse élargit la fonction des gains du capital humain. L’équation élémentaire d’estimation utilisée dans le cadre de cette recherche est une régression logistique de la probabilité de trouver du travail à partir de variables exogènes correspondant à diverses caractéristiques individuelles, locales ou propres au ménage :

1. Variables démographiques : âge, état civil, nombre d’enfants, nombre d’enfants d’âge scolaire et d’enfants de 4 ans ou moins.
2. Catégorie d’immigration : variables dichotomiques égales à l’unité si les principaux demandeurs sont des travailleurs qualifiés, conjoints ou personnes à charge d’un travailleur qualifié, réfugiés ou autres, avec la catégorie du regroupement familial comme catégorie de référence.
3. Région de naissance : variables dichotomiques égales à l’unité si le RL est né en Asie-Pacifique, Amérique centrale ou du Sud, dans un pays d’Europe autre que le Royaume-Uni ou un pays d’Europe occidentale, en Afrique ou au Moyen-Orient. Les RL nés en Amérique du Nord, au Royaume-Uni et en Europe occidentale forment le groupe de référence.
4. Province de résidence : variables dichotomiques égales à l’unité si le RL vivait dans l’une des provinces de l’Atlantique, au Québec, dans l’une des provinces des Prairies ou en Colombie-Britannique. Les RL vivant en Ontario forment le groupe de référence. Une variable dichotomique égale à l’unité si le RL vivait dans une région autre que les cinq principales RMR (régions métropolitaines de recensement), soit Toronto, Montréal, Vancouver, Ottawa et Calgary. L’inclusion de ces variables vise à saisir les différences locales du marché du travail.
5. Groupe ethnique : variables dichotomiques égales à l’unité si le RL appartient à l’un des groupes suivants : Chinois, Asiatiques du Sud, Noirs, Philippins, Latino-Américains, Asiatiques de l’Ouest, Arabes, Asiatiques d’autres régions (Asiatiques du Sud-Est, Coréens, Japonais) ou est issu d’une autre minorité visible. Les Blancs forment le groupe de référence.
6. Scolarité : variables dichotomiques égales à l’unité si le RL détient un diplôme de maîtrise, un diplôme universitaire ou un peu de formation universitaire, un peu de formation postsecondaire quelconque, un diplôme d’études secondaires ou moins, avec un baccalauréat comme catégorie de référence; variable dichotomique égale à l’unité si le RL faisait des études au moment de l’entrevue.
7. Langues : variables dichotomiques égales à l’unité si le RL connaît l’anglais (parle assez bien, bien, très bien l’anglais et ayant l’anglais pour langue maternelle) ou le français (parle assez bien, bien, très bien le français et ayant le français pour langue maternelle).
8. Expérience : temps passé au Canada mesuré en mois et un ensemble de variables dichotomiques égales à l’unité si le RL avait une expérience de travail avant d’immigrer, était venu au Canada auparavant, avait travaillé au Canada en vertu d’un permis de travail, avait étudié au Canada en vertu d’un permis d’études et avait un emploi réservé au Canada à son arrivée.
9. Variables de capital social : indicateurs de capital social précisé dans la partie 4.1. Voir le tableau A.1 pour plus de détails. De plus, la situation d’emploi du conjoint est susceptible de déterminer son attachement au marché du travail et ses possibilités d’emploi; il constitue donc une variable explicative et entre dans la catégorie des facteurs familiaux.

5.2.1 Modèles de données de panel

Cette étude table sur la dimension longitudinale de l’ELIC pour présenter des analyses longitudinales selon un modèle de données de panel, en plus d’analyses transversales. Les modèles de données de panel tiennent compte d’effets latents individuels précis, ce qui règle les problèmes de variables omises en modélisation transversale. L’avantage essentiel d’un ensemble de données de panel sur une coupe transversale est qu’il permet la modélisation des différences de comportement entre les individus. Un échantillon constant typique comporte de nombreuses unités transversales et seulement quelques périodes, comme les microdonnées de l’ELIC. Aussi les techniques de modélisation des données recueillies au moyen d’un panel portent-elles principalement sur l’hétérogénéité des unités plutôt que sur des autocorrélations de séries chronologiques.

Le cadre de base des modèles de données de panel binaires est un modèle à équation unique :

où i constitue un indice des unités transversales et t, un indice des périodes de temps. Dans la présente analyse, T = 3. Il y a p variables indépendantes observables dans X_it, lesquelles varient ou non dans le temps. L’effet latent individuel z_i rend l’hétérogénéité, qui détermine chez les individus la probabilité de trouver du travail, et comprend un ensemble de facteurs spécifiques individuels non observables, notamment des différences sur le plan de la personnalité, des aptitudes ou de la santé, des caractéristiques propres à la famille ou au groupe, des attitudes culturelles relatives à la participation au marché du travail, etc. Lorsque z_i ne contient qu’un terme constant, le modèle est de type transversal ordinaire. Lorsque z_i contient des variables latentes, une estimation transversale combinée entraînera des estimations biaisées et incompatibles en raison de l’omission de variables (l’hétérogénéité par exemple); les modèles de données de panel sont donc plus appropriés.

1) Le modèle logit à effets fixes

Le modèle logit à effets fixes pose que les effets individuels latents z_i sont corrélés avec X_it, ce qui modifie le modèle de la façon suivante :

où F est la courbe logistique cumulative F(a) = exp(a) / (1+exp(a)).

Le modèle à effets fixes comporte néanmoins des avantages, notamment ceux d’accroître la marge de manœuvre et de tenir compte du caractère dépendant des variables explicatives. En régression logistique, cependant, le modèle à effets fixes donnerait lieu à des estimations incompatibles en raison d’un prétendu problème de paramètres incidents⁷, particulièrement lorsque T_i est fixe et court, comme c’est le cas dans la présente analyse, où T_i = 3. De plus, les effets fixes font reposer l’inférence sur une comparaison intra-individuelle de la situation d’emploi plutôt qu’interindividuelle, si bien que les effets fixes sont aussi appelés effets intrasujets. Aussi l’estimation ne tient-elle compte que des observations relatives aux individus dont la situation d’emploi a changé, si bien que les estimateurs présentent un léger biais d’échantillonnage (léger T_i). Par ailleurs, l’utilisation du modèle à effets fixes ne me permet pas d’estimer les effets des variables qui ne varient pas dans le temps, mais qui m’intéressent, notamment la catégorie d’immigration et le groupe ethnique. Entre-temps, le modèle à effets fixes ne servirait qu’à traiter des échantillons équilibrés auxquels il ne manque pas de données.

2) Le modèle logit à effets aléatoires

Nous utilisons un modèle à effets aléatoires lorsque nous présumons que les effets individuels non observés z_i du modèle général (1) ne présentent pas de lien avec les variables explicatives observées X_it: Cov (X_it, z_i) = 0, t = 1, 2,…, T, si bien que la distribution conditionnelle f (z_i | X_it) est indépendante pour X_it. On obtient le modèle à effets aléatoires suivant :

E (v_it | X_it) = 0,

Les variables qui ne varient pas dans le temps comme la catégorie d’immigration, le groupe ethnique et le lieu de naissance peuvent être comprises dans la régression sous X_it, ce que ne permet pas le modèle à effets fixes. Selon l’hypothèse des effets aléatoires, les effets individuels sont nullement corrélés avec les variables explicatives observées. Cette vision conviendrait si les unités transversales de l’échantillon provenaient d’une vaste population, ce qui est le cas des données longitudinales utilisées pour cette recherche. L’estimateur des effets aléatoires est plus efficace que celui des effets fixes. Or, comme l’hypothèse impose une lourde restriction sur la distribution de l’hétérogénéité, les estimations risquent d’être contradictoires si l’hypothèse est inappropriée.

3) Modèle logit avec moyenne de population au moyen d’équations d’estimations généralisées (EEG)

Proposée par Zeger, Liang et Albert (1988), la méthode des équations d’estimations généralisées est une solution de rechange aux hypothèses à effets aléatoires. Le modèle EEG pour un résultat exprimé de façon binaire est un prolongement du modèle standard de régression logistique issu de l’approche du modèle linéaire généralisé.

Les modèles basés sur les EEG conviennent lorsque l’accent est mis sur les inférences à l’égard de la moyenne de population. Dans cette recherche, la différence moyenne entre des groupes disposant d’un stock de capital social plus ou moins imposant est beaucoup plus importante que la différence entre deux immigrants. De plus, les modèles fondés sur les EEG pourraient tenir compte de la méthodologie de l’enquête en incluant le coefficient de pondération dans les régressions. Ainsi, si les estimations de modèles logit combinés, de modèle logit à effets fixes ou aléatoires et de modèle logit basé sur les EEG sont comparées dans le tableau des résultats, ce dernier modèle sert de référence pour une étude approfondie des effets attribuables au temps et aux groupes.

Notes

5. Montgomery insiste sur les avantages du réseau, pour l’employeur, par rapport à d’autres voies de recrutement puisque le réseau permet de filtrer les candidats peu compétents.

6. Pour une explication détaillée de leurs propositions, voir Calvó-Armengol et Jackson (2004).

7. Voir l’exposé de Greene (2003), chapitre 21, à ce sujet.

8. Neuhaus, Kalbfleisch et Hauck (1991) proposent un exposé approfondi comparant l’approche basée sur l’EEG et les approches disciplinaires (estimation d’effets aléatoires et d’effets fixes) aux fins d’analyses des résultats binaires à partir de données longitudinales.

• Précédent
• 1
• 2
• 3
• 4
• 5
• 6
• 7 (présent)
• 8
• 9
• 10
• 11
• 12
• Suivant