Explication des calculateurs de moisissures et de durée de vie
Avis de non-responsabilité
Les renseignements contenus dans ce document sont basés sur la compréhension actuelle des problèmes soulevés. Ils ne s’appliquent pas nécessairement à toutes les situations, et aucune des activités décrites n’assure une protection complète. Bien que des efforts raisonnables aient été faits pour s’assurer que les renseignements sont exacts et à jour, l’éditeur, l’Institut canadien de conservation (ICC), n’offre aucune garantie à cet égard et n’assume aucune responsabilité en cas de perte, de réclamation ou de revendication pouvant résulter, directement ou indirectement, de l’utilisation des renseignements ou de la confiance qui leur est accordée. L’ICC ne cautionne aucun des produits, services ou matériaux indiqués dans ce document ou sur les sites Web externes auxquels ce document pourrait renvoyer. Par ailleurs, il ne fait aucune déclaration à leur sujet. Ces produits, services ou matériaux sont donc utilisés à vos propres risques.
Sur cette page
- Liste des abréviations
- Explication du Calculateur de moisissures
- Explication du Calculateur de durée de vie
- Deux règles empiriques simples à suivre avant de commencer
- La notion de durée de vie des objets
- Données historiques sur les durées de vie de référence
- Catégories logarithmiques pour la durée de vie des matériaux
- Graphique de l’effet de la température sur la durée de vie
- Graphique de l’effet de l’humidité relative sur la durée de vie
- Courbe de l’effet de la température et de l’humidité relative sur la durée de vie
- Scénarios complexes dans ClimaSpec
- Équations de la durée de vie
- Bibliographie
Liste des abréviations
- ASHRAE
- American Society of Heating, Refrigerating and Air-Conditioning Engineers
- HR
- humidité relative
- ICC
- Institut canadien de conservation
- ICOM-CC
- Comité pour la conservation du Conseil international des musées
- IPI
- Image Permanence Institute
- ISO
- Organisation internationale de normalisation
Explication du Calculateur de moisissures
Stefan Michalski et Tom Strang
Sources des données et établissement des équations
La figure 1 présente les données de plusieurs auteurs sur le temps nécessaire à la croissance des moisissures. La ligne bleue continue est une courbe ajustée par Michalski (1993) d’après les données de Snow et coll. (1944) sur le temps nécessaire à l’apparition de mycélium visible sur de l’herbe séchée, du tourteau de lin et de la farine d’os (points noirs). Parmi les denrées alimentaires qu’ont étudiées Snow et coll., celles-ci sont les plus représentatives d’une large classe d’objets de musée, cellulosiques et protéiques. Ces données et la courbe ajustée (ligne bleue pleine) figurent dans des publications antérieures de l’Institut canadien de conservation (ICC), comme la figure 4 dans Agent de détérioration : humidité relative inadéquate et le Bulletin technique 23 Directives concernant l’humidité et la température dans les archives du Canada. La figure 1 est tirée des éditions de 1999 à 2023 du chapitre « Museums, Galleries, Archives, and Libraries » du manuel de l’ASHRAE Handbook: Heating, Ventilating, and Air-Conditioning Applications. L’équation de l’humidité relative (HR) pour cette courbe (indiquée dans la légende, en haut à droite) sert à calculer le « temps probable nécessaire à la formation de moisissures perceptibles » dans le Calculateur de moisissures de ClimaSpec, qui se trouve dans le menu de gauche.

© Gouvernement du Canada, Institut canadien de conservation. 132715-0020
Figure 1. Relation entre l’HR et le temps (en jours) nécessaire à la croissance des moisissures.
Description de la figure 1
Le graphique de la figure 1 contient deux courbes. L’axe vertical indique, sur une échelle logarithmique de 0,1 à 3 000, le nombre de jours nécessaires à la croissance des moisissures. L’axe horizontal représente une échelle linéaire de 50 % à 100 % d’HR. Les courbes sont toutes deux lisses et partent de 65 % d’HR, en haut à gauche, et descendent pour s’aplatir à 100 %, en bas à droite. Des groupes de points de données correspondent à chaque courbe, décrite dans le texte principal. Le tableau 1 présente une sélection de points clés sur les deux courbes.
Plus récemment, Strang (2012) a compilé davantage de données issues de recherches utilisant des supports conçus pour maximiser la croissance des moisissures, notamment la gélatine. La gélatine est la couche sensible aux moisissures dans les matériaux photographiques, la toile encollée des tableaux et leurs rentoilages, ainsi que les papiers encollés. La figure 1 résume les principaux points de sa compilation. Les lignes verticales noires indiquent les plages de temps de fructification rapportées pour chaque valeur d’HR. Elles suivent la double ligne rouge pour le mycélium visible, dans la mesure où la fructification se produirait après la croissance du mycélium, c’est-à-dire qu’elle prendrait un peu plus de temps (elle serait supérieure à la double ligne rouge). Les données de germination (un grand nuage dans les graphiques originaux de Strang) sont représentées ici par le bord extérieur de ce nuage, indiquant les temps les plus courts rapportés pour la germination à chaque valeur d’HR (les croix blanches). La ligne tiretée bleue est ajustée de manière à se situer juste à l’extérieur de ces croix blanches. Le calculateur utilise l’équation pour cette ligne tiretée bleue (décrite dans la légende, dans le coin supérieur droit) afin d’indiquer le temps probable le plus court pour la germination des spores.
| Limites extérieures | HR de 64 % | HR de 65 % | HR de 70 % | HR de 75 % | HR de 80 % | HR de 85 % | HR de 90 % | HR de 100 % |
|---|---|---|---|---|---|---|---|---|
| Limite extérieure de la fructification | Aucune depuis plus de 1 000 jours | 500 | 130 | 35 | 12 | 5 | 3 | 2 |
| Limite extérieure de la germination | Aucune depuis plus de 1 000 jours | 600 | 50 | 12 | 1,5 | 0,5 | 0,2 | 0,2 |
Remarque : Les nombres du tableau 1 ont été arrondis à un ou à deux chiffres significatifs.
Humidité relative statique et humidité relative dynamique
Sedlbauer (2001) a développé un modèle dynamique pour la croissance des moisissures dans des conditions fluctuantes, modèle qui a été incorporé dans le logiciel de performance des bâtiments connu sous le nom de WUFI (Wärme Und Feuchte Instationär/transport transitoire de chaleur et d’humidité; en anglais seulement). De tels modèles dynamiques dépassent la portée du Calculateur de moisissures dans ClimaSpec. Nous examinons plutôt les conditions statiques en utilisant les données de nombreuses études dans lesquelles on a maintenu une HR constante, comme il est indiqué à la figure 1, ainsi qu’une température constante.
De manière prudente, on peut appliquer le calculateur à deux conditions fluctuantes. Si l’HR est fluctuante mais toujours supérieure à 65 %, on entre, dans le calculateur, l’HR des périodes les plus humides. (Cela fournit une valeur prudente : le temps le plus court possible pour la croissance.) Si et quand l’HR descend sous 65 % et y demeure suffisamment longtemps pour que les matériaux atteignent l’équilibre avec cette HR plus faible, alors toute moisissure qui se développerait pourrait être considérée comme morte. (Le cycle de croissance doit recommencer à partir des spores lorsque l’HR dépasse 65 %.)
Approche multitactique pour une prévention pratique des moisissures
La conservation préventive contre les moisissures présente de multiples facettes. Il est rare (mais pas impossible) qu’un taux d’HR élevé se manifeste de manière uniforme et stable dans toute une pièce. La présence de moisissure est généralement un événement localisé, déclenché par des sources d’eau externes, la condensation, une mauvaise ventilation, un emballage inapproprié, des gradients de température, etc. (consulter les figures 5 et 6 dans Agent de détérioration : humidité relative inadéquate). La propreté des objets joue également un rôle, non seulement sur le plan des spores mais sur le plan des nutriments qui favorisent la croissance des moisissures. Des méthodes pour contrôler ces facteurs et bien d’autres sont décrites en détail dans le Bulletin technique 26 Prévention des moisissures et récupération des collections : lignes directrices pour les collections du patrimoine.
Problèmes de santé
Les moisissures constituent un grand risque pour les occupants de l’espace, et pas seulement pour les collections. Si vous êtes aux prises avec des problèmes de moisissure, consulter dès que possible le Bulletin technique 26 Prévention des moisissures et récupération des collections : lignes directrices pour les collections du patrimoine. Pour obtenir de plus amples renseignements sur les problèmes de santé liés aux moisissures, ainsi que sur les nombreuses situations qui favorisent les moisissures dans les bâtiments, consulter Adan et Samson (2011).
Explication du Calculateur de durée de vie
Stefan Michalski
Cette section offre une description du contexte technique entourant le Calculateur de durée de vie qui fait partie de ClimaSpec. Ce calculateur fournit des estimations quant à la durée de vie des objets organiques qui se décomposent rapidement en raison de processus chimiques à des températures et à une HR modérées, ainsi que les améliorations possibles au moyen de diverses combinaisons de conditions plus froides ou plus sèches. (Une partie du contenu des sections suivantes est apparue en premier dans l’édition de 2019 du chapitre de l’American Society of Heating, Refrigerating and Air-Conditioning Engineers [ASHRAE], préparé par l’auteur à titre de membre du comité responsable de ce chapitre. Ces renseignements ont été révisés ici.)
Les estimations de la durée de vie des objets à température ambiante, listées dans le tableau 2 et fournies dans ClimaSpec, peuvent varier. La durée de vie peut être jusqu’à trois fois plus courte ou plus longue que celle indiquée pour chaque objet. De même, lors du choix d’une température plus basse et d’une HR inférieure, même en utilisant les meilleurs modèles et données accessibles, l’amélioration de la durée de vie ultérieure peut différer de la prédiction. Cela est principalement dû à l’incertitude de l’énergie d’activation, comme l’illustrent les zones ombrées de la figure 2. Malgré cette incertitude, les calculateurs des avantages sur la durée de vie d’une mise en réserve dans des conditions froides ou au sec sont considérés comme utiles par les auteurs cités, ainsi que par les établissements de recherche qu’ils représentent.
Deux règles empiriques simples à suivre avant de commencer
Avant de décrire les graphiques, les calculateurs et les équations, une simple règle empirique permet de quantifier l’enjeu : une baisse de température de 5 °C (par exemple, de 21 °C à 16 °C) double la durée de vie de l’objet. Cela est vrai pour les matériaux qui se dégradent rapidement en raison de processus chimiques dans des conditions normales de mise en réserve (comme le papier de mauvaise qualité, de nombreux films photographiques et les bandes et disques magnétiques). Une autre baisse de 5 °C double à nouveau la durée de vie de l’objet. Ainsi, une baisse de 21 °C à 11 °C quadruple la durée de vie, et ainsi de suite. À l’inverse, chaque augmentation de 5 °C réduit la durée de vie de moitié.
Une seconde règle empirique est qu’une réduction de moitié de l’HR (par exemple, de 50 % à 25 %) double (ou plus) la durée de vie de l’objet (Michalski, 2002).
Ces règles empiriques peuvent servir de base à l’étude de la mise en réserve à une température contrôlée. Cependant, le calcul de scénarios saisonniers complexes dans un contexte d’économies d’énergie est nécessaire lorsqu’il s’agit de trouver le juste équilibre entre les coûts de la préservation et la durabilité ou encore de prendre en compte les répercussions d’une exposition intermittente à des conditions chaudes ou d’un traitement antiparasitaire à haute température. Le Calculateur de durée de vie dans ClimaSpec répond à ce besoin.
La notion de durée de vie des objets
Le Calculateur de durée de vie produit trois résultats :
- une durée de vie de référence pour l’objet sélectionné à une température modérée (environ 20 °C) et à une HR modérée (environ 50 %);
- le multiplicateur de durée de vie pour un scénario ayant une température et une HR données;
- le produit des deux premiers résultats, c’est-à-dire la durée de vie prévue pour le scénario sélectionné.
L’expression « durée de vie » a une signification claire et sans ambiguïté (plus ou moins) dans le cas des humains. En revanche, pour les objets qui se détériorent, cette notion est plus ambiguë. Pour la préciser, nous devons faire trois jugements difficiles :
- Quelle est la valeur culturelle ou l’utilité de l’objet (par exemple, les objets d’art ayant une valeur esthétique ou les documents conservés en tant que dossiers d’information)?
- Existe-t-il des caractéristiques mesurables qui affectent la valeur, comme le jaunissement, la perte de solidité ou la perte de lisibilité?
- Quel est le critère de perte inacceptable d’une caractéristique particulière (par exemple, un jaunissement inacceptable empêchant une utilisation en exposition ou une solidité insuffisante du document empêchant sa consultation directe par les chercheurs)?
Ces définitions sont sans ambiguïté pour quelques types d’objets patrimoniaux seulement. Par exemple, lorsque les supports numériques ou magnétiques deviennent illisibles, il est clair que leur utilité archivistique en tant que support d’information est « morte ». Le Calculateur de durée de vie dans ClimaSpec fournit toujours une description de la caractéristique qui est attribuée à l’estimation de la durée de vie et, dans la mesure du possible, de ses répercussions sur l’utilité de l’objet. Cependant, il faut toujours interpréter la perte d’utilité et de valeur dans son propre contexte. Une cassette vidéo illisible peut être morte pour une archive, et partiellement morte pour une installation vidéo dans un musée, mais encore utile dans une salle d’exposition qui présente la technologie que l’on pouvait retrouver dans une maison des années 1980.
Pour justifier et concevoir la mise en réserve au froid, on pourrait éviter toute incertitude concernant ces jugements culturels et se contenter de prendre en considération l’amélioration relative de la durée de vie de la collection que fournissent des conditions plus froides et plus sèches, par exemple « 10 fois plus longue » (ce que donne le Calculateur de durée de vie). Cependant, étant donné les coûts de mise en réserve dans des conditions plus froides et plus sèches, il reste à déterminer si, sans ce type de mise en réserve, la durée de vie des objets deviendrait alors trop courte au regard du mandat de préservation de l’établissement. Dans un autre cas, il faudra déterminer si la durée de vie de certains matériaux sera considérablement réduite à l’aide d’un traitement antiparasitaire à haute température.
Dans les établissements d’archives, il est devenu courant d’utiliser des chambres froides pour des collections entières (les films photographiques en sont un exemple). Ce n’est pas le cas dans les musées, ce qui peut entraîner la détérioration de nombreux objets du XXe siècle au cours de la vie d’un conservateur. Ces objets comprennent le caoutchouc, le celluloïd, les acétates, les mousses de polyuréthane, les photographies en couleurs, etc. (consulter la colonne de droite du tableau 2).
Données historiques sur les durées de vie de référence
Les données de référence du tableau 2 ont été compilées pour la première fois dans le Bulletin technique 23 Directives concernant l’humidité et la température dans les archives du Canada. Cette publication contient également des notes et références détaillées sur la plupart des matériaux présentés dans le tableau. Lorsque le tableau a été préparé pour la ressource de l’ICC Agent de détérioration : température inadéquate, des documents non archivistiques ont été ajoutés. Cependant, les entrées relatives aux disques optiques ont été supprimées, car des estimations plus précises de la durée de vie se trouvent dans la Note de l’ICC 19/1 Durabilité des CD, des DVD et des disques Blu-ray inscriptibles. Les durées de vie vont de 5 ans à plus de 100 ans, selon le processus de fabrication.
La version finale du tableau est utilisée ailleurs sur le site Web de l’ICC et a également été incluse dans les éditions de 2019 et de 2023 du manuel de l’ASHRAE, dans le chapitre « Museums, Galleries, Archives, and Libraries ».
Dans ClimaSpec, les durées de vie de référence fournies sont basées sur ces sources et d’autres.
| Durée de vie de référence | Matériaux |
|---|---|
| 1 000 ans |
|
| 300 ans |
|
| 100 ans |
|
| 30 ans |
|
Catégories logarithmiques pour la durée de vie des matériaux
On décrit généralement notre vie et les événements historiques en unités temporelles linéaires et uniformes, exprimées en années ou en décennies. Cela ne fonctionne pas bien pour catégoriser la durée de vie chimique des matériaux, qu’il vaut mieux exprimer sous forme de multiples. Par exemple, chaque catégorie peut être plusieurs fois plus longue que sa voisine. La question qui se pose alors est la suivante : Dans quelle mesure pouvons-nous séparer de telles catégories avec précision? L’ICC a constaté que les catégories du tableau 2 (30 ans, 100 ans, 300 ans et 1 000 ans) suffisent pour les généralisations pratiques. En termes techniques, ces catégories suivent une échelle logarithmique (base 10), avec deux échelons pour chaque unité logarithmique. Le point médian entre 1 et 10 est 10½ = 3,16, valeur arrondie à 3 pour plus de simplicité.
Pour quelques matériaux bien étudiés, comme le papier et les pellicules photographiques, si l’on connaît l’acidité et que l’on a une définition nette de leur fin de vie, on peut être en mesure de faire des prédictions plus précises que ce qu’indiquent ces catégories logarithmiques. En général, dire qu’un matériau tel que le papier acide est dans le groupe des 100 ans dans le tableau 2 signifie que sa durée de vie est probablement d’environ 100 ans. Cependant, elle peut être inférieure ou supérieure d’un facteur de trois. Ainsi, chaque catégorie présente une incertitude qui s’étend à ses catégories adjacentes.
Graphique de l’effet de la température sur la durée de vie
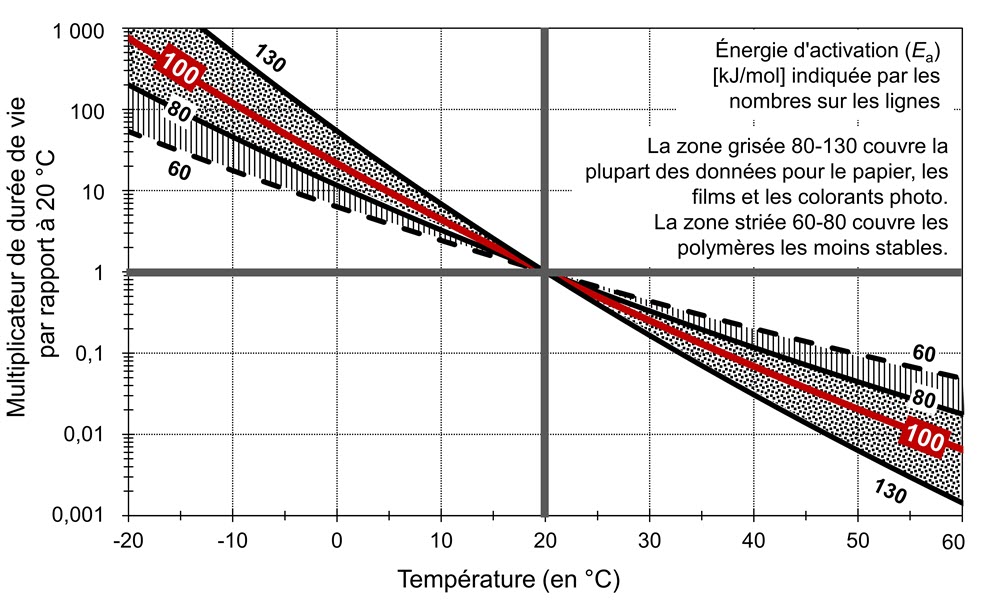
Le paramètre chimique clé pour prédire l’effet du changement de température sur le multiplicateur de durée de vie est l’énergie d’activation (Ea). Une compilation des énergies d’activation des matériaux organiques présents dans les collections patrimoniales (Reilly et coll., 1995; Nishimura, 1996; Michalski, 2002), comme le papier, les films, les colorants photographiques, les supports magnétiques et les vernis en résine, montre que pour plus des trois quarts des matériaux étudiés, l’énergie d’activation se situe dans une plage de 80 kJ/mol à 120 kJ/mol. Une étude récente de la dégradation thermique de la résistance du bois donne une valeur Ea = 85 kJ/mol, ce qui est également dans cette plage (Froidevaux et Navi, 2013). Plus récemment encore, on a mesuré des valeurs de 93 kJ/mol à 130 kJ/mol dans différents papiers d’impression modernes. Sur la figure 2, cette plage complète de 80 kJ/mol à 130 kJ/mol est représentée par la zone grisée.
On peut aussi calculer théoriquement cette plage d’énergies d’activation sans tenir compte de matériaux en particulier, si ce n’est en précisant que le processus chimique prend au moins plusieurs décennies pour arriver à terme aux températures ambiantes (Michalski, 2002). Ainsi, les données empiriques et la théorie semblent indiquer que cette plage d’énergies d’activation peut servir de valeur universelle pour les matériaux patrimoniaux, comme ceux qui figurent dans le tableau 3. La valeur médiane de cette plage, soit 100 kJ/mol, un chiffre rond pratique, a été choisie pour les graphiques des multiplicateurs de durée de vie dans le Bulletin technique 23 Directives concernant l’humidité et la température dans les archives du Canada.
© Gouvernement du Canada, Institut canadien de conservation. 132715-0022
Figure 2. Relation entre la durée de vie et la température selon différentes énergies d’activation (Ea).
Description de la figure 2
Le graphique de la figure 2 contient quatre courbes. L’axe vertical représente une échelle logarithmique du multiplicateur de durée de vie par rapport à 20 °C. L’axe horizontal représente la température en degrés Celsius. Les quatre courbes sont toutes des courbes régulières qui s’étendent du coin supérieur gauche au coin inférieur droit et se croisent à 20 °C et à une durée de vie de 1.
| Énergie d’activation (Ea) en kJ/mol | -20 °C | -10 °C | 0 °C | 5 °C | 10 °C | 15 °C | 20 °C | 25 °C | 30 °C | 60 °C |
|---|---|---|---|---|---|---|---|---|---|---|
| 130 | 5 500 | 500 | 54 | 20 | 7 | 2,6 | 1 | 0,4 | 0,2 | 0,002 |
| 100 | 750 | 120 | 20 | 10 | 4 | 2,1 | 1 | 0,5 | 0,3 | 0,007 |
| 80 | 200 | 45 | 12 | 6 | 3 | 1,8 | 1 | 0,6 | 0,3 | 0,02 |
| 60 | 60 | 20 | 6 | 4 | 2 | 1,6 | 1 | 0,7 | 0,4 | 0,05 |
Remarque : Les nombres du tableau 3 ont été arrondis à un ou à deux chiffres significatifs.
Pour les matériaux qui se dégradent de manière importante en quelques décennies ou moins, comme le polyuréthane de polyester qui peut se désintégrer en poudre (c’est d’ailleurs le maillon faible des supports magnétiques, et c’était un matériau populaire auprès des artistes à la fin du XXe siècle) ou les vernis à base de résine naturelle qui jaunissent de manière inacceptable, les énergies d’activation tombent dans une plage inférieure de 60 kJ/mol à 80 kJ/mol (Michalski, 2000), indiquée par la zone rayée de la figure 2.
Graphique de l’effet de l’humidité relative sur la durée de vie
Bien que tous les auteurs s’accordent sur le rôle de la température et de l’énergie d’activation dans le calcul du multiplicateur de durée de vie, il existe une variété de modèles permettant de calculer l’effet de l’HR. Tous s’accordent à dire qu’une faible HR diminue la vitesse de désintégration, mais l’ampleur exacte de cette valeur reste incertaine, simplement parce qu’il n’y a pas assez de données expérimentales pour confirmer un modèle plutôt qu’un autre.
Les cinq modèles les plus connus, par ordre chronologique, sont les suivants (le fondement technique de chaque modèle est examiné dans une section ultérieure, Équations de la durée de vie) :
- Le travail de pionnier de Sebera (1994), popularisé dans un rapport pour la Commission on Preservation and Access. Il a inventé le terme « isoperme » pour désigner les lignes de même durée de vie dans les graphiques, comme sur la figure 4.
- L’indice de préservation de l’Image Permanence Institute (IPI), initialement fourni sous la forme d’une roue de préservation, désormais accessible dans une application Web, eClimateNotebook (en anglais seulement). L’outil est basé sur le tableau des multiplicateurs de Reilly et coll. (1995).
- Les équations et les tableaux publiés dans le Bulletin technique 23 Directives concernant l’humidité et la température dans les archives du Canada.
- Les équations et les graphiques publiés dans des articles de revues par des chercheurs de l’University College London et des Archives nationales de Londres (Strlič et coll., 2015).
- Des chercheurs de l’ICC et du Centre de recherche sur la conservation (Paris) ont publié des équations et des graphiques pour des types précis de papiers d’impression (Tétreault et coll., 2023). Ces équations et graphiques sont également offerts sous forme d’un outil de calcul (Outil de calcul de la permanence du papier), qui se trouve sur la page Outils de conservation préventive.
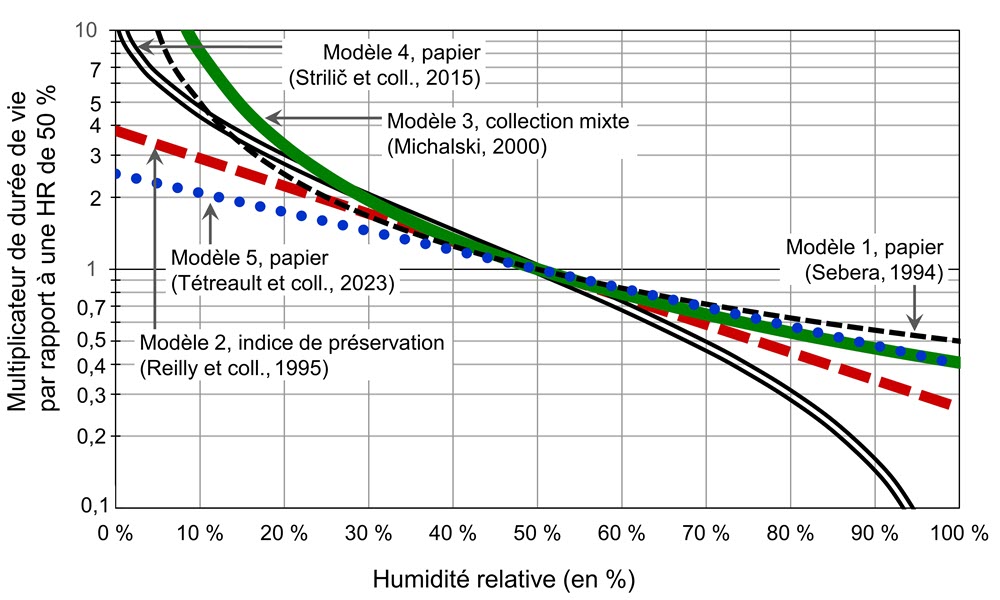
Les prédictions des cinq modèles concernant l’effet de l’HR sur la durée de vie par rapport à la durée de vie pour une HR de 50 % sont représentées sur la figure 3. Dans la région ayant une HR de 30 % à 60 %, les modèles se chevauchent sans différences pratiques dans leurs prédictions. Le passage de 50 % à 25 % d’HR augmente la durée de vie de deux fois ou un peu plus pour tous les modèles, comme le donne à penser la règle empirique. De toute façon, on doit éviter les conditions supérieures à 60 % d’HR pour réduire le risque que les couches de gélatine des photographies collent aux surfaces adjacentes et le risque de moisissure, qui commence à 65 % d’HR (consulter le Calculateur de moisissures dans ClimaSpec). En général, il faut éviter les conditions inférieures à 25 % d’HR afin de réduire le risque de déformation ou de fracture.
En résumé, les cinq modèles donnent des prédictions similaires dans la région qui est considérée comme pratique pour la plupart des collections. Cela dit, l’éventuelle dessiccation massive de collections, comme les piles de journaux, qui peuvent tolérer une HR inférieure à 25 % (ce qui serait beaucoup moins énergivore qu’une mise en réserve au froid équivalente) sera mieux prédite par le modèle le plus apte à prédire les multiplicateurs de durée de vie en dessous de 25 % d’HR.
© Gouvernement du Canada, Institut canadien de conservation. 132715-0023
Figure 3. Effet de l’HR sur le multiplicateur de durée de vie, par rapport à une HR de 50 % et à une température de 20 °C environ, selon cinq modèles.
Description de la figure 3
Le graphique de la figure 3 contient cinq courbes. L’axe vertical représente une échelle logarithmique de la durée de vie à une HR de 50 %. L’axe horizontal représente l’HR. Les cinq courbes sont toutes des courbes régulières qui s’étendent du coin supérieur gauche au coin inférieur droit et se croisent à une HR de 50 % et à un multiplicateur de durée de vie de 1. Les courbes correspondent aux modèles 1, 2, 3, 4 et 5.
| Modèle | HR de 10 % | HR de 20 % | HR de 30 % | HR de 40 % | HR de 50 % | HR de 60 % | HR de 70 % | HR de 80 % |
|---|---|---|---|---|---|---|---|---|
| 1 Sebera | 5,0 | 2,5 | 1,7 | 1,3 | 1 | 0,83 | 0,71 | 0,62 |
| 2 Reilly et coll. | 2,9 | 2,2 | 1,7 | 1,3 | 1 | 0,77 | 0,59 | 0,45 |
| 3 Michalski | 8,1 | 3,3 | 1,9 | 1,3 | 1 | 0,79 | 0,65 | 0,54 |
| 4 Strlič et coll. | 4,6 | 2,9 | 2,0 | 1,4 | 1 | 0,70 | 0,48 | 0,30 |
| 5 Tétreault et coll. | 2,1 | 1,7 | 1,4 | 1,2 | 1 | 0,82 | 0,68 | 0,57 |
Courbe de l’effet de la température et de l’humidité relative sur la durée de vie
Sebera (1994), le premier auteur à proposer une représentation graphique de la relation entre la durée de vie, la température et l’HR, a utilisé un graphique rectangulaire, comme le montre la figure 4, et appelé « isopermes » les lignes de durée de vie constante. Strlič et coll. (2015) ont proposé le terme « isochrones ». La figure 4 présente les modèles actuels 2, 3, 4 et 5. Bien que les auteurs du modèle 5 proposent des Ea différentes pour différents types de papiers d’impression, leur modèle est tracé selon une Ea égale à 101 kJ/mol. Il s’agit, selon les auteurs, de l’Ea du papier journal acide.
Ces quatre modèles donnent des résultats presque identiques dans la plage pratique d’HR (de 60 % à 30 %) et dans la majorité de la plage pratique de températures. Le modèle de l’IPI prédit que les températures peuvent être jusqu’à trois degrés de moins que les deux autres modèles pour la même durée de vie, mais ce n’est pas une différence significative lorsqu’on décide d’adopter la mise en réserve au frais ou au froid.
Plutôt que le seul modèle de l’ICC, les quatre modèles actuels (2, 3, 4 et 5) sont présentés aux figures 4 et 5 et dans les tableaux connexes, ainsi que sous Équations de la durée de vie, et ce, pour deux raisons. D’abord pour fournir au lecteur une comparaison impartiale des modèles actuels; ensuite, pour montrer que si les différences sont intéressantes pour les chercheurs, les conclusions sont identiques sur le plan pratique : dans la mesure du possible, il faut recourir à la mise en réserve au frais ou au froid pour les objets qui se dégradent rapidement.
La figure 5, qui représente un diagramme psychrométrique, est une autre méthode de représentation graphique des multiplicateurs de durée de vie (isopermes et isochrones). Ce graphique montre la manière classique dont les ingénieurs représentent la température et l’HR lors de la conception de systèmes. L’axe horizontal représente la température et l’axe vertical représente le poids de la vapeur d’eau dans l’air (humidité absolue). Les valeurs d’HR constituent un ensemble de lignes courbes (de 10 % jusqu’à 100 %, soit l’HR maximale).
Si l’on veut, par exemple, trouver des combinaisons de température et d’HR qui donnent des durées de vie, pour les matériaux, 10 fois plus grandes que celles indiquées dans le tableau 2, il faut rechercher les courbes « ×10 » sur la figure 4 ou 5 (ou dans la colonne « ×10 » du tableau 5). On constatera alors que pour une HR de 50 %, les trois modèles se situent entre 3 °C et 5 °C, donc environ 4 °C. Si l’on choisit une HR de 30 %, le multiplicateur ×10 se situe alors entre 7 °C et 9 °C, donc environ 8 °C.
© Gouvernement du Canada, Institut canadien de conservation. 132715-0025
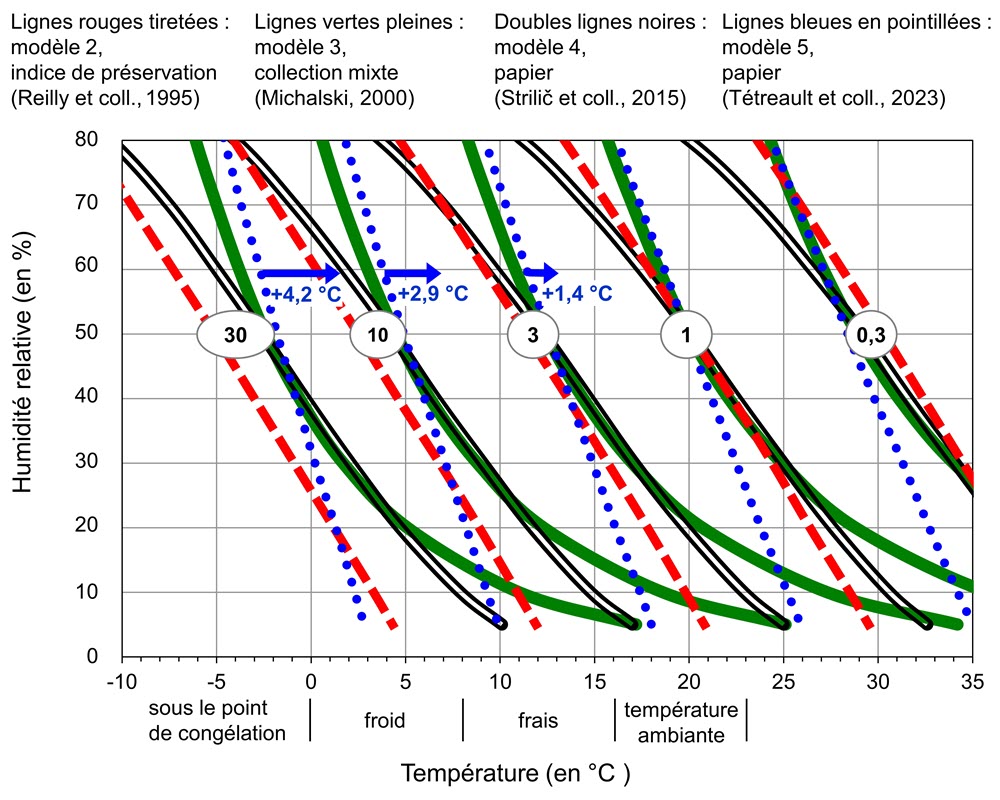
Figure 4. Multiplicateurs de durée de vie (isopermes et isochrones) pour les modèles 2, 3, 4 et 5, tracés selon des coordonnées rectangulaires de température et d’HR. (Le modèle 5 est tracé selon le papier journal que les auteurs ont analysé et dont l’Ea est de 101 kJ/mol. Les flèches bleues montrent le décalage avec les autres types de papiers analysés, qui ont une Ea de 127 kJ/mol.) Les plages de température intitulées « sous le point de congélation » « froid », « frais » et « température ambiante » sont celles définies dans les normes ISO pour le stockage de différents types de supports (ISO, 2011).
Description de la figure 4
Le graphique de la figure 4 contient cinq groupes de quatre courbes chacun. L’axe vertical représente l’HR. L’axe horizontal représente la température en degrés Celsius. Les cinq groupes sont approximativement parallèles. Les courbes sont régulières et fortement inclinées vers le bas. Chacun des cinq groupes est désigné par un multiplicateur de durée de vie relative, allant d’un minimum de ×0,3 à un maximum de ×30. Les quatre courbes « ×1 » passent toutes par le point 20 °C pour une HR de 50 %.
| Multiplicateur de durée de vie | ×0,3 pour les modèles 2, 3, 4 et 5 | ×1 pour les modèles 2, 3, 4 et 5 | ×3 pour les modèles 2, 3, 4 et 5 | ×10 pour les modèles 2, 3, 4 et 5 | ×30 pour les modèles 2, 3, 4 et 5 |
|---|---|---|---|---|---|
| HR de 10 % | 39, 46, 40, 34 | 29, 36, 31, 25 | 20, 27, 23, 17 | 11, 19, 15, 9 | 3, 11, 8, 2 |
| HR de 20 % | 37, 38, 37, 33 | 26, 29, 28, 24 | 18, 21, 20, 16 | 9, 12, 12, 8 | 1, 5, 5, 1 |
| HR de 30 % | 35, 34, 34, 31 | 24, 25, 25, 23 | 16, 17, 17, 15 | 7, 9, 9, 7 | -1, 2, 2, 0 |
| HR de 40 % | 32, 31, 32, 30 | 22, 22, 23, 21 | 14, 14, 15, 14 | 5, 6, 7, 6 | -3, -1, 0, -1 |
| HR de 50 % | 30, 29, 29, 28 | 20, 20, 20, 20 | 11, 12, 12, 13 | 3, 5, 4, 5 | -5, -2, -3, -2 |
| HR de 60 % | 28, 27, 27, 27 | 18, 18, 18, 19 | 9, 11, 10, 11 | 0, 3, 2, 4 | -7, -4, -5, -3 |
| HR de 70 % | 26, 26, 24, 26 | 16, 17, 15, 17 | 7, 10, 7, 10 | -2, 2, -1, 3 | -9, -5, -7, -4 |
Remarques :
- Certaines valeurs indiquées dans le tableau 5 dépassent l’échelle des figures 4 et 5.
- Le modèle 5 est tracé selon le papier journal que les auteurs ont analysé et dont l’Ea est de 101 kJ/mol.
© Gouvernement du Canada, Institut canadien de conservation. 132715-0027
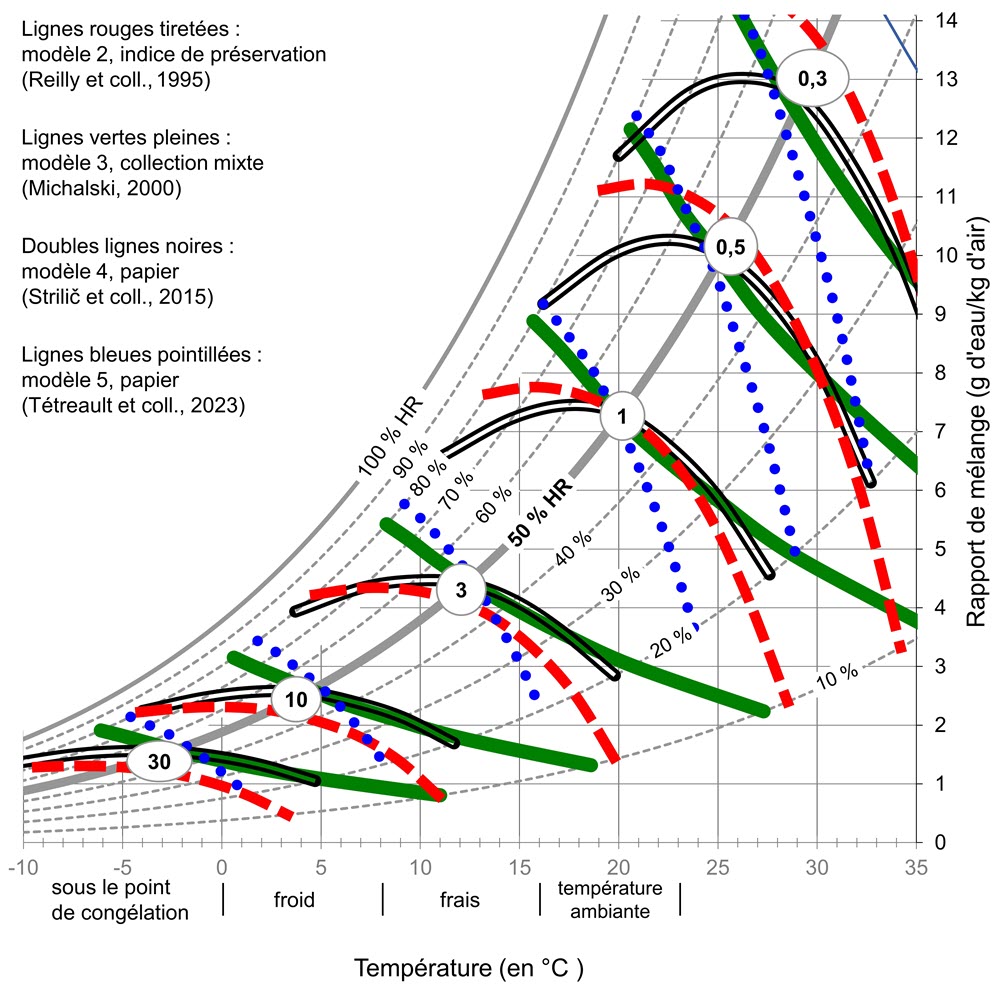
Figure 5. Multiplicateurs de durée de vie des modèles 2, 3, 4 et 5 reportés sur le graphique psychrométrique. Les plages de température « sous le point de congélation », « froid », « frais » et « température ambiante » sont celles définies dans les normes de l’ISO relatives au stockage des supports. (Dans les éditions de 2019 et de 2023 du chapitre de l’ASHRAE, une erreur d’impression a fait disparaître les lignes du modèle 3 de la figure.)
Description de la figure 5
Le graphique de la figure 5 contient six groupes de quatre courbes. L’axe horizontal représente la température en degrés Celsius. L’axe vertical représente le rapport de mélange, en grammes d’eau par kilogramme d’air. Les lignes d’HR, de 10 % à 100 %, s’incurvent doucement vers le haut sur ces axes et forment un ensemble de coordonnées de fond pour les courbes principales. Les six groupes de quatre courbes sont courbés de façon régulière. Chaque groupe est désigné par un multiplicateur de durée de vie relative, allant d’un minimum de ×0,3 à un maximum de ×30. Les quatre courbes « ×1 » passent toutes par le point 20 °C et une HR de 50 %.
Scénarios complexes dans ClimaSpec
Le Calculateur de durée de vie de ClimaSpec présente plusieurs avantages par rapport aux graphiques et aux tableaux :
- Il permet de saisir des scénarios complexes avec des réductions saisonnières sur une base mensuelle pour réaliser des économies d’énergie.
- Il permet de calculer l’effet d’un retrait occasionnel d’objets mis en réserve dans des conditions plus chaudes ou plus humides.
- Il emploie des valeurs spécifiques de l’énergie d’activation pour le matériau, lorsque ces valeurs existent.
Le Calculateur de durée de vie choisit par défaut le modèle 3, conformément aux autres publications de l’ICC.
Équations de la durée de vie
Tous les calculateurs de durée de vie proposés dans la documentation scientifique sur la science de la conservation reconnaissent que, pour les matériaux organiques qui se décomposent rapidement en raison de leur instabilité chimique (comme les matériaux figurant dans la colonne de droite du tableau 2), le mécanisme en cause est l’hydrolyse acide. Elle augmente avec l’acidité du matériau, l’HR et la température. La durée de vie peut être exprimée comme le produit de trois fonctions (f) : une fonction dépendant de l’acidité du matériau, une fonction dépendant de la température et une fonction dépendant de l’HR ou, pour certains auteurs, du paramètre connexe, soit la teneur en humidité.
Équation 1 : tDV = C * f(pH) * f(T) * f(HR, TH)
Où
C = constante pour chaque matériau (en unités de temps)
pH = acidité du matériau
tDV= durée de vie (en unités de temps)
T = température (en kelvins)
HR = humidité relative (sans dimension)
TH = teneur en humidité (du matériau) [sans dimension]
L’équation de la durée de vie en fonction de la température (le deuxième terme de l’équation 1), du nom de son découvreur, Svante Arrhenius, est utilisée depuis plus d’un siècle en génie chimique. En termes de durée de vie (plutôt que de la réciproque, soit la vitesse de réaction), l’équation d’Arrhenius est la suivante :
Équation 2 : f(T) = exp(Ea /(R*T))
Où
R = constante des gaz parfaits (constante de Boltzmann) [8,314 J/(mol K)]
Ea = énergie d’activation (en J/mol)
Pour faciliter la comparaison, les propositions des cinq auteurs concernant la durée de vie en fonction de l’HR et de la température ont été réarrangées sous la même forme générale de l’équation 1. Si nous présentons ces cinq propositions, ce n’est pas pour indiquer une quelconque préférence ni pour critiquer leur validité respective. Chacune d’elles a été publiée dans des revues avec comité de lecture au cours des 30 dernières années. Le but est plutôt de montrer que, malgré les différences dans la façon dont elles sont établies et dans les matériaux décrits, leurs prédictions quant aux avantages de la mise en réserve au frais et au froid convergent vers des plages utiles pour les gestionnaires de collections.
Dans chacune des équations suivantes, la constante (C) a été fixée de manière que l’équation donne le multiplicateur de durée de vie (tMDV) par rapport à la durée de vie à 20 °C et à 50 % d’HR. Pour plus de clarté, le terme d’énergie d’activation a été placé entre accolades { }.
Modèle 1
Bien qu’il ne soit pas représenté sur les figures 4 et 5, le modèle d’isopermes de Sebera (1994) est mentionné ici pour son importance historique dans le domaine de la préservation des archives. Sebera a utilisé une forme modifiée de l’équation d’Arrhenius, qui inclut une seconde dépendance à la température placée à l’extérieur de l’exponentielle. Les auteurs ultérieurs l’ont omise, car elle a un effet relativement mineur. Pour l’énergie d’activation, Sebera a examiné les données disponibles pour le papier et a proposé une plage entre deux valeurs : 125 kJ/mol et 146 kJ/mol (25 et 35 dans ses unités originales de kCal/mol). Ses estimations de Ea sont supérieures aux valeurs actuellement acceptées (issues d’études ultérieures), de sorte que ses isopermes exagèrent les avantages de la mise en réserve au froid. En l’absence de toute donnée contraire, il a supposé que la durée de vie était simplement proportionnelle à l’HR. L’équation de Sebera devient alors :
Équation 3 : tMDV= C * 1/T * exp[{125 ou 146}/(R*T)] * (1/HR)
Où
tMDV = multiplicateur de durée de vie, par rapport à une valeur de 1 °C à 20 °C et à une HR de 50 %
Modèle 2
Les auteurs (Reilly et coll., 1995) ont établi les paramètres à partir de nombreuses données sur les films en acétate. Les équations n’ont pas été publiées telles quelles, mais le tableau publié de multiplicateurs de durée de vie produit par les auteurs peut être ajusté à l’équation suivante. Le terme HR comporte une petite correction de température. L’équation de Reilly et coll. est la suivante :
Équation 4 : tMDV = 4,69E–17 * exp[{94,9}/(R*T)] * exp[HR * (0,02087 *T – 8,79)]
Modèle 3
L’auteur (Michalski, 2000) a calculé l’énergie d’activation à la suite d’un vaste examen de données pour le papier, les films et les colorants. La dépendance à l’égard de l’HR a été calculée à partir d’une nouvelle analyse (Michalski, 1993) de nombreuses données sur le vieillissement du papier à plusieurs valeurs d’HR, produite par Graminski et coll. (1978). L’équation de Michalski devient alors :
Équation 5 : tMDV = 6,17E–19 * exp[{100}/(R*T)] * (1/HR)1,3
Modèle 4
Les auteurs (Strlič et coll., 2015) ont établi les équations à partir de leurs nombreuses données sur les papiers neufs et anciens. Le terme HR comporte une petite correction de température. L’équation de Strlič et colll. est la suivante :
Équation 6 : tMDV = 9,468E–21 * exp[{119}/(R*T)]
* exp[–36,72 * {ln(1 – HR)/ (1,67*T – 741,82)}(1/(5,7622 – 0,012*T))]
Bien que l’équation 6 complète soit utilisée pour les figures 4 et 5, il est instructif de voir à quoi ressemble le modèle 4 s’il est ajusté à une équation de la même forme que celle des modèles 1, 2 et 3. Dans toute la plage pratique des valeurs d’HR (20 % à 60 %) et de températures (20 °C à -10 °C), l’équation suivante donne des résultats à 10 % près des résultats de l’équation 6 en utilisant une énergie d’activation (Ea) de 100 kJ/mol :
Équation 7 : tMDV = 1,00E–17 * exp[{100}/(R*T)] * exp[–3,7*HR]
Modèle 5
Les auteurs (Tétreault et coll., 2023) ont établi une équation à partir d’une étude sur les papiers d’impression modernes. Bien que l’acidité (pH) ait joué un rôle clé dans la durée de vie des types de papiers analysés, ils ont découvert qu’une équation pour les multiplicateurs de durée de vie pouvait être indépendante de l’acidité. Leur principale conclusion est que différents groupes de papiers d’impression modernes ont des Ea suffisamment différentes (97 kJ/mol à 130 kJ/mol) pour qu’il soit utile de prendre en compte ces différences, comme le permet l’Outil de calcul de la permanence du papier, qui est basé sur leur modèle et qui se trouve sur la page Outils de conservation préventive. Leur équation pour les isopermes, soit la durée de vie relative, est la suivante (Tétreault et coll., 2023; équation 14) :
Équation 8 : tMDV = 2,46 * exp[(0,572-0,00822*T)HR] * exp[({Ea}]/R)*(1/T – 1/293,15)
Pour les figures et tableaux du présent document, et dans un souci de comparaison généralisée entre les modèles, leur modèle est calculé selon une Ea de 101 kJ/mol, soit leur valeur pour le papier journal acide.
En résumé, lorsqu’on utilise une équation de la même forme que l’équation 1, les modèles 2, 3, 4 et 5 semblent tous indiquer une énergie d’activation très similaire (Ea), autour de 95 à 101 kJ/mol. Le modèle 5 suggère des valeurs plus élevées pour certains types de papiers d’impression.
Toutefois, pour ce qui est de l’effet de l’HR, il existe des différences significatives entre les modèles pour les valeurs inférieures à 20 % et ceux pour les valeurs supérieures à 60 %. Il n’y a pas assez de données à ces extrêmes d’HR pour déterminer lequel est correct. Parmi les différents modèles, le terme HR diffère de deux façons. Tout d’abord, Reilly et coll. (1995), Strlič et coll. (2015) et Tétreault et coll. (2023) partent du principe que la variable fondamentale est la teneur en humidité, qui dépend à son tour de l’HR, mais uniquement lorsqu’elle est ajustée pour différentes températures. Ensuite, Sebera (1994) et Michalski (2000) supposent que l’HR est le paramètre fondamental. Une différence plus importante, cependant, est le choix de la fonction : certains auteurs utilisent une fonction exponentielle (Reilly et coll., 1995; Strlič et coll., 2015; Tétreault et coll., 2023). D’autres (Michalski, 1993, 2000 et 2002; Sebera, 1994; Erhardt et Mecklenburg, 1995; et Zou et coll., 1996) utilisent une loi de puissance (qui inclut l’utilisation de Sebera de l’indice 1, soit la dépendance linéaire). Dans les modèles utilisant une fonction exponentielle, curieusement, l’hydrolyse se poursuit à une HR de 0 % (c’est-à-dire sans humidité), alors qu’avec une loi de puissance, l’hydrolyse s’arrête en l’absence d’humidité, d’où la divergence rapide des modèles à une HR inférieure à 20 % (ainsi qu’à une HR supérieure à 60 %) dans les graphiques des figures 4 et 5. Comme nous l’avons noté précédemment, cette divergence n’a pas d’incidence pratique, puisque personne ne recommande actuellement la mise en réserve à des pourcentages d’HR aussi faibles (ou à des pourcentages d’humidité élevée), mais elle devient pertinente lorsqu’il s’agit d’expliquer la mesure dans laquelle la faible HR des bâtiments non humidifiés en hiver a profité aux collections d’objets acides dans le passé et pourrait encore le faire à l’avenir.
Bibliographie
Adan, O. C. G., et R. A. Samson (directeurs de publication). Fundamentals of Mold Growth in Indoor Environments and Strategies for Healthy Living, Wageningen (Pays-Bas), Wageningen Academic, 2011.
American Society of Heating, Refrigerating and Air-Conditioning Engineers. « Museums, Galleries, Archives, and Libraries », dans ASHRAE Handbook: Heating, Ventilating, and Air-Conditioning Applications (sous la direction de M. S. Owen) Atlanta (Géorgie), ASHRAE, 2019, p. 24.1-24.46.
American Society of Heating, Refrigerating and Air-Conditioning Engineers. « Museums, Galleries, Archives, and Libraries », dans ASHRAE Handbook: Heating, Ventilating, and Air-Conditioning Applications (sous la direction de M. S. Owen) Atlanta (Géorgie), ASHRAE, 2023, p. 24.1-24.47.
Erhardt, D., et M. F. Mecklenburg. « Accelerated VS Natural Aging: Effect of Aging Conditions on the Aging Process of Cellulose », Materials Research Society Online Proceedings Library, vol. 352 (1995), p. 247-270.
Froidevaux, J., et P. Navi. « Aging Law of Spruce Wood », Wood Material Science & Engineering, vol. 8, no 1 (2013), p. 46-52.
Graminski, E. L., E. J. Parks et E. E. Toth. NBSIR 78-1443, The Effects of Temperature and Moisture on the Accelerated Aging of Paper (format PDF; en anglais seulement), Washington (D.C.), National Bureau of Standards Polymer Division, 1978.
Iraci, J. Durabilité des CD, des DVD et des disques Blu-ray inscriptibles, version révisée, Notes de l’ICC 19/1, Ottawa (Ontario), Institut canadien de conservation, 2019.
Michalski, S. « Relative Humidity: A Discussion of Correct/Incorrect Values », dans ICOM-CC 10th Triennial Meeting, Washington, D.C., 22–27 August 1993: Preprints (sous la direction de J. Bridgland) Comité pour la conservation du Conseil international des musées, 1993, p. 624-629.
Michalski, S. Directives concernant l’humidité et la température dans les archives du Canada, Bulletin technique 23, Ottawa (Ontario), Institut canadien de conservation, 2000.
Michalski, S. « Double the Life for Each Five-Degree Drop, More than Double the Life for Each Halving of Relative Humidity », dans ICOM-CC 13th Triennial Meeting, Rio de Janeiro, Brazil, 22–27 September 2002: Preprints (sous la direction de R. Vontobel), London (Royaume-Uni), James & James, 2002, p. 66-72.
Nishimura, D. W. « The Practical Presentation of Research Studies on Film Stability », dans Research Techniques in Photographic Conservation: Proceedings of the Conference in Copenhagen, 14–19 May 1995 (sous la direction de M. S. Koch), Copenhagen (Danemark), The Royal Danish Academy of Fine Arts, 1996, p. 85-92.
Nishimura, D. W. Understanding Preservation Metrics (format PDF; en anglais seulement), Rochester (New York), Image Permanence Institute/Rochester Institute of Technology, 2018.
Organisation internationale de normalisation. ISO 18934:2011, Matériaux pour l’image – Archives multimédia – Environnement de stockage, Genève (Suisse), Organisation internationale de normalisation, 2011.
Reilly, J. M., D. W. Nishimura et E. Zinn. New Tools for Preservation: Assessing Long-Term Environmental Effects on Library and Archives Collections, Washington (D.C.), Commission on Preservation and Access, 1995.
Sebera, D. K. Isoperms: An Environmental Management Tool (en anglais seulement), Washington (D.C.), Commission on Preservation and Access, 1994.
Sedlbauer, K. Prediction of Mould Fungus Formation on the Surface of and Inside Building Components (format PDF; en anglais seulement), Fraunhofer Institute for Building Physics (2001), p. 75-141.
Snow, D. « The Germination of Mould Spores at Controlled Humidities », Annals of Applied Biology, vol. 36, no 1 (1949), p. 113.
Snow, D., M. H. G. Crichton et N. C. Wright. « Mould Deterioration of Feeding-Stuffs in Relation to Humidity of Storage: Part I. The Growth of Moulds at Low Humidities », Annals of Applied Biology, vol. 31, no 2 (1944), p. 102-110.
Strang, T. Studies in Pest Control for Cultural Property, thèse de doctorat, Université de Gothenburg, 2012.
Strlič, M., et coll. « Damage Function for Historic Paper. Part III: Isochrones and Demography of Collections », Heritage Science, vol. 3, no 1 (2015), p. 1-11.
Tétreault, J., D. Vedoy, P. Bégin, S. Paris Lacombe et A.-L. Dupont. « Modelling the Degradation of Acidic and Alkaline Printing Paper », Cellulose, vol. 30, no 17 (novembre 2023), p. 11157-11175.
Zou, X., T. Uesaka et N. Gurnagul. « Prediction of Paper Permanence by Accelerated Aging I. Kinetic Analysis of the Aging Process » (en anglais seulement), Cellulose, vol. 3 (1996), p. 243-267.
© Gouvernement du Canada, Institut canadien de conservation, 2025
Publié par :
Institut canadien de conservation
Ministère du Patrimoine canadien
1030, chemin Innes
Ottawa (Ontario) K1B 4S7
Canada
No de catalogue : CH57-4/83-2025F-PDF
ISBN 978-0-660-75637-0